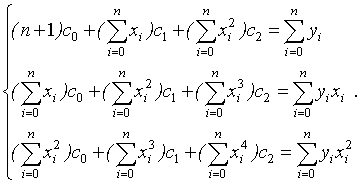|
 (2.37)
|
|
3. Описание программного средства
3.1 Спецификация
переменных, процедур и функций
Void XY_print() - Функция очищает экран и рисует координатные оси.
double P (double *vek, int m, double xx) - функция для вычисления значения многочлена.
double Q (double *a, int m) - функция, возвращающая среднеквадратическое отклонение со
входным параметром - вектором значений *a.
void draw (double *X, int col, int count, double q) - функция, выводящая график функции аппроксимированной по методу
наименьших квадратов полиномом; входные данные - вектор значений *X, цвет col, целое число count и значение
среднеквадратического отклонения q.
double lsolve (double
**array, double *vek, int nn, double *X) - функция, решающая СЛАУ
методом Гаусса.mnk (double m, int
color) - функция, аппроксимирующая функцию y=f(x) методом наименьших квадратов
_mnk() - Функция
аппроксимирует данные моделью: y(t)=x1+x2*t+x3*sin(t) по методу наименьших квадратов.menu() - функция вывода меню на
экран.main() - главная функция.
3.2 Схемы алгоритмов
double mnk (double m,
int color)
double _mnk()
4. Расчеты в системы Mathcad
4.1 Контрольный пример
работы
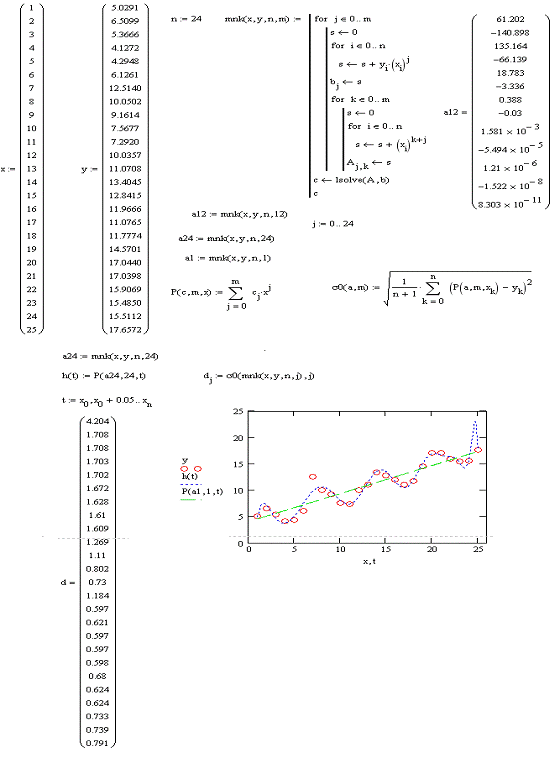
Рисунок 1 - Метод наименьших
квадратов
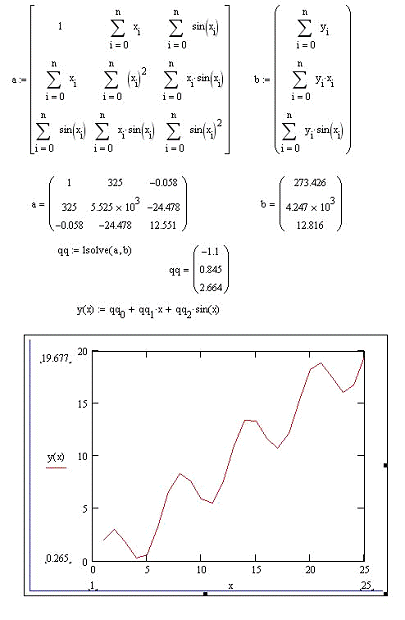
Рисунок 2 - Аппроксимация моделью: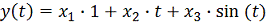 
, по методу наименьших квадратов.
4.2 График в среде в
программирования
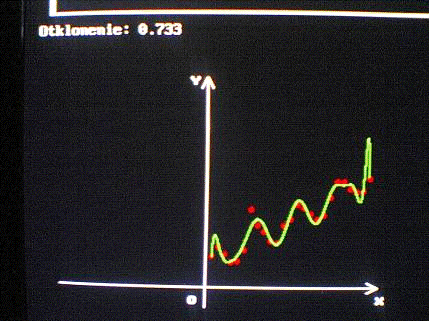
Рисунок 3 - Метод наименьших
квадратов
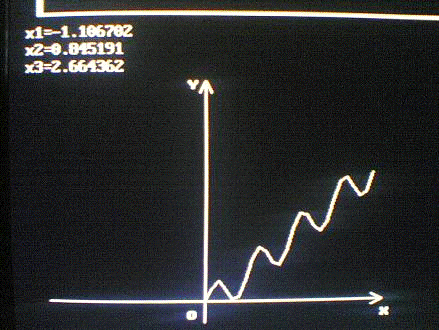
Рисунок 4 - Метод наименьших
квадратов моделью
Заключение
Проанализировав решение системы в MathCAD, можно сделать вывод,
что решение, полученное с помощью программы правильное, так как графики
практически совпадают по форме и по значениям.
Список использованных
источников
2. Лапчик М.П. Численные методы: Учебное пособие для вузов /
Рагулина М.И., Хеннер Е.К.; под редакцией Лапчика М.П.: Издательский центр
«Академия», 2004. - 384 с.
. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. - Численные
методы (2 изд.).
. Тарасов В.Н. Численные методы, теория, алгоритмы,
программы: Учебное пособие для вузов / Бахарева Н.Ф; под редакцией Тарасова
В.П.: Издательский центр Оренбург: ИПК ОГУ, 2003. - 100 с.
Приложение А
Текст программы
#include <iostream.h>
#include
<graphics.h>
#include <conio.h>
#include <stdio.h>
#include
<string.h>
#include <math.h>
#include
<stdlib.h>
init_graph() {gdriver =
DETECT, gmode, errorcode;(&gdriver, &gmode, «»);=
graphresult();(errorcode!= grOk) {(«Graphics error:%s\n»,
grapherrormsg(errorcode));(«Press any key to halt:»);();(1);
}
}
n=25;x[n]={1. 0,2. 0,3.
0,4. 0,5. 0,6. 0,7. 0,8. 0,9. 0,10. 0,11. 0,12. 0,13. 0,14.0,
. 0,16. 0,17. 0,18.
0,19. 0,20. 0,21. 0,22. 0,23. 0,24. 0,25.0};y[n]={5. 0291,6. 5099,5. 3666,4.
1272,4. 2948,6. 1261,12. 5140,10. 0502,9. 1614,7. 5677,7. 2920,10.
0357,11.0708,
. 4045,12. 8415,11.
9666,11. 0765,11. 7774,14. 5701,17. 0440,17. 0398,15. 9069,15. 4850,15.
5112,17.6572};
menu_output()
{<<» ╔════════════════════════════════════════════════════════════════════════════╗\n\r»;<<»
║ 0. Approx. model (y(t)=x1+x2*t+x3*sin(t)) ║\n\r»;<<» ║
1. Real grafik ║\n\r»;<<» ║ 2. Grafik po MNK ║\n\r»;<<»
║ 3. Ochistit' ║\n\r»;<<» ╠════════════════════════════════════════════════════════════════════════════╣\n\r»;<<»
║ ESC - Exit ║\n\r»;<<» ╚════════════════════════════════════════════════════════════════════════════╝\n\r»;0;
}
XY_print() { // Вырисовка осей(0,0,1);(0);(1,0);(WHITE);(0,0,680,459);(20,380,320,380);(160,400,160,180);(320,380,310,375);(320,380,310,385);
(160,180,155,190);(160,180,165,190);(145,180,
«Y»);(320,390, «X»);(145,390, «0»);
}
p_pixel (double x,
double y, int col) {(x+160, - y+380, col);
}
P (double *vek, int m,
double xx) { // Значение многочленаtem=0;(int i=0; i<m; i++)(! i) tem+=vek[i];tem+=vek[i]*pow (xx,
i);
return tem;
}
Q (double *a, int m) { // значение
среднеквадратичного отклонение многочлена P
double temp=0;(int i=0;
i<n; i++) temp+=pow((P (a, m, x[i]) - y[i]), 2);=temp/n;=sqrt(temp);=ddd
[m-1];temp;
}
draw (double *X, int
col, int count, double q) { // рисует график
по
MNK(1,0);<<«Otklonenie: «<<q<<endl;y, temp;(double xx=1;
xx<=25; xx+=0.001) {=0;(int t=0; t<count; t++)(! t) y+=X[t];y+=X[t]*pow
(xx, t);_pixel (xx*6, y*6, col);
}
}
// -Решение СЛАУ методом Гауса-
lsolve (double **array,
double *vek, int nn, double *X) {*IOR=new int[nn];i, l, k, M, j, p;AKK, AMAIN,
delitel;(k=0; k<nn; k++) IOR[k]=k;
// -Нахождение индекса-(k=0;
k<nn; k++) {
AKK=0;(i=k; i<nn;
i++) {=IOR[i];(fabs (array[l] [k])<AKK) continue;=l; p=i; AKK=fabs (array[l]
[k]);
}
// -Меняем места-=array[M]
[k];(k!=p) {IOR[p]=IOR[k]; IOR[k]=M;};
// -Прямой ход-(j=k; j<nn;
j++) array[M] [j]=array[M] [j]/AMAIN;[M]=vek[M]/AMAIN;(i=k+1; i<nn; i++)
{=IOR[i];=array[l] [k];(j=k; j<nn; j++) array[l] [j]=array[l] [j] -
delitel*array[M] [j];[l]=vek[l] - delitel*vek[M];
}
}
// -Обратный ход-sum;(k=nn-1;
k>=0; k-) {=IOR[k];=0;(j=k+1; j<nn; j++) sum=sum+array[l]
[j]*X[j];[k]=vek[l] - sum;
}[] IOR;*X;
}
mnk (double m, int
color) { // Наименьших квадратов**A=new double *[n];(int i=0; i<n; i++) A[i]=new double
[m];*b=new double [m];s=0;(int j=0; j<m; j++) {=0;(int i=0; i<n; i++) {(!
j) s+=y[i];s+=y[i]*pow (x[i], j);
}[j]=s;(int k=0; k<m;
k++) {=0;(i=0; i<n; i++)(! (k+j)) s+=1;s+=pow (x[i], k+j);[j] [k]=s;
}
}*X=new double [m];
*X=lsolve (A, b, m, X);
//if (m==25) {X=a25;}(X, color, m, Q (X, 25));[] A;[] X;[] b; 0;
}
double _mnk() { // Аппроксимация данных моделью (y(t)=x1+x2*t+x3*sin(t) по mnkm=13;*X=new double[m];**A=new double *[n];(int i=0; i<n;
i++) A[i]=new double [m];*b=new double [m];s=0;(int j=0; j<m; j++) {=0;(int
i=0; i<n; i++) {(! j) s+=y[i];s+=y[i]*pow (x[i], j);
}[j]=s;(int k=0; k<m;
k++) {=0;(i=0; i<n; i++)(! (k+j)) s+=1;s+=pow (x[i], k+j);[j] [k]=s;
}
}
*X=lsolve (A, b, m,
X);();_print();_output();**matr=new double*[3];(i=0; i<3; i++) matr[i]=new
double[3];*bb=new double[3];*cc=new double[3];
[0] [0]=1;(i=0; i<n;
i++) matr[0] [1]+=x[i];(i=0; i<n; i++) matr[0] [2]+=sin (x[i]);(i=0; i<n;
i++) b[0]+=p (A, 15, i);
(i=0; i<n; i++)
matr[1] [0]+=x[i];(i=0; i<n; i++) matr[1] [1]+=x[i]*x[i];(i=0; i<n; i++)
matr[1] [2]+=x[i]*sin (x[i]);(i=0; i<n; i++) bb[1]+=x[i]*p (A, 15, i);
(i=0; i<n; i++)
matr[2] [0]+=sin (x[i]);(i=0; i<n; i++) matr[2] [1]+=x[i]*sin (x[i]);(i=0;
i<n; i++) matr[2] [2]+=sin (x[i])*sin (x[i]);(i=0; i<n; i++) bb[2]+=p (A,
15, i)*sin (x[i]);
*cc=lsolve (matr, bb, 3,
cc);<< «x1=»<<cc[0]<<endl;<<
«x2=»<<cc[1]<<endl;<< «x3=»<<cc[2]<<endl;yy,
yy1;=0;
(double xx=1; xx<=25;
xx+=1) {=cc[0]+cc[1]*xx+cc[2]*sin(xx);(xx*6+160, - yy*6+380, (xx-1)*6+160, -
yy1*6+380);=yy;_pixel (xx*6, yy*6,2);
} [] A;[] X;[]
b;0;
}
real_graph()
{(4);(1,0);(0,0,3);(RED);(int i=0; i<n; i++)(x[i]*6+160, - y[i]*6+380,1);
}
main()
{ch;();_graph();_print();_output();
{=getch();(ch)
{'0':
}(ch==27)
{(0);
}
} while (ch!=27);
return 0;
}