Основы изучения темы 'Многогранники'
Оглавление
математический геометрия
преподавание многогранник
Введение . Теоретические основы
изучения темы «Многогранники»
. Исторические аспекты
. Понятие многогранников
. Свойства многогранников .
Использование моделирования при изучении темы «Многогранники»
. Геометрическое моделирование -
неотъемлемая часть современного математического образования
. Федоровские модели пространства
. Общие вопросы применения
изображений пространственных фигур в преподавании геометрии
. Изображения в систематическом курсе
геометрии. Типичные ошибки. Методические аспекты изложения темы «Многогранники»
в школьном курсе
. Обзор изложения темы
«Многогранники» в учебниках разных авторов
. Виды и роль наглядных средств при
изучении многогранников
.Опорные задачи по теме «Многогранники»
. Изучение свойств многогранников
Заключение
Литература
Приложение 1
Приложение 2
Введение
Тема «Многогранники» одна из основных в
традиционном курсе школьной геометрии. Они составляют, можно сказать,
центральный предмет стереометрии. Изучение параллельных и перпендикулярных
прямых и плоскостей, двугранных углов и другое, так же как введение векторов и
координат,- все это только начала стереометрии, подготовка средств для
исследования ее более содержательных объектов - главным образом тел и поверхностей.
Центральная роль многогранников определяется,
прежде всего, тем, что многие результаты, относящиеся к другим телам,
получаются исходя из соответствующих результатов для многогранников; Достаточно
вспомнить определение объемов тел и площадей поверхностей путем предельного
перехода от многогранников.
Кроме того, многогранники сами по себе
представляют чрезвычайно содержательный предмет исследования, выделяясь среди
всех тел многими интересными свойствами, специально к ним относящимися
теоремами и задачами. Можно, например, вспомнить теорему Эйлера о числе граней,
ребер и вершин, симметрию правильных многогранников, вопрос о заполнении
пространства многогранниками и др.
Многогранникам должно быть уделено в школьном
курсе больше внимания еще и потому, что они дают особенно богатый материал для
развития пространственных представлений, для развития того соединения живого
пространственного воображения со строгой логикой, которое составляет сущность
геометрии. Уже самые простые факты, касающиеся многогранников, требуют такого
соединения, которое оказывается при этом не совсем легким делом. Даже такой
простой факт, как пересечение диагоналей параллелепипеда в одной точке, требует
усилия воображения, чтобы его увидеть наглядно, и нуждается в строгом доказательстве
[Саакян С.М., 2000].
Более того, использование многогранников с
самого начала изучения стереометрии служит различным дидактическим целям. На
многогранниках удобно демонстрировать взаимное расположение прямых и плоскостей
в пространстве, показывать применение признаков параллельности и
перпендикулярности прямых и плоскостей в пространстве. Иллюстрация первых
теорем стереометрии на конкретных моделях повышает интерес учащихся к предмету.
Также одной из основных задач обучения
математики является развитие у учащихся абстрактного мышления. Этой цели в
значительной мере способствует применение наглядных пособий, причем не только в
младших классах, но и в старших. Широкие возможности для реализации этой цели
предоставляет тема «Многогранники», в частности, самостоятельное изготовление
учениками наглядных пособий. В процессе изготовления моделей многогранников,
кроме теоретических знаний и навыков, ученики закрепляют сформировавшиеся новые
понятия при помощи чертежа и фактического решения задач на построение. При
самостоятельном изготовлении моделей образ создается по частям, в силу этого с
ними можно производить различные манипуляции. При этом все их свойства и
особенности легко познаются и прочно закрепляются в памяти учащихся [Стройк
Д.Я., 1969].
Цель работы: рассмотреть особенности
использования моделей при решении стереометрических задач (на примере изучения
темы «Многогранники»).
Задачи работы:
) рассмотреть подходы к основным определениям
данной темы: многогранника, выпуклого многогранника, правильного многогранника;
) изучить изложение данной темы в школьных
учебниках;
) выделить средства, которые могут быть
применены при изучении многогранников;
) изучить особенности использования моделей при
решении стереометрических задач (на примере изучения темы «Многогранники»)
) подобрать основные задачи для решения по
данной теме;
) разработать серию уроков с использованием
моделей при решении стереометрических задач.
Гипотеза исследования: изучение темы
«Многогранники» в школе будет более успешным, если при подготовке к урокам и
проведении них учитель математики будет использовать модели при решении
стереометрических задач:
Объект исследования: методика изучения
многогранников
Предмет исследования: модели при решении
стереометрических задач
I. Теоретические основы изучения
темы «Многогранники»
. Исторические аспекты
Начиная с 7 века до нашей эры в Древней Греции
создаются философские школы, в которых происходит постепенный переход от
практической к философской геометрии. Большое значение в этих школах приобретают
рассуждения, с помощью которых удалось получать новые геометрические свойства.
Одной из первых и самых известных школ была
Пифагорейская, названная в честь своего основателя Пифагора
Отличительным знаком пифагорейцев была
пентаграмма, на языке математики - это правильный невыпуклый или звездчатый
пятиугольник. Пентаграмма, на языке математики - это правильный невыпуклый или
звездчатый пятиугольник
Пентаграмме присваивалось способность защищать
человека от злых духов. Существование только пяти правильных многогранников
относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали,
что материя состоит из четырех основных элементов: огня, земли, воздуха и воды
[Ходеева Т. 2002].
Согласно их мнению, атомы основных элементов
должны иметь форму различных Платоновых тел
Дальнейшее развитие математики связано с именами
Платона, Кеплера, Евклида и
Архимеда. Все использовали в своих философских
теориях правильные многогранники.
Платоновыми телами называются правильные
однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и
углы которых равны, причем грани - правильные многоугольники. К каждой вершине
правильного многогранника сходится одно и то же число рёбер. Все двугранные
углы при рёбрах и все многогранные углы при вершинах правильного многоугольника
равны.
Платоновы тела - трехмерный аналог плоских
правильных многоугольников.
Существует лишь пять выпуклых правильных
многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб
(гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Доказательство этого факта известно уже более двух тысяч лет; этим
доказательством и изучением пяти правильных тел завершаются "Начала"
Евклида.
Также существует семейство тел, родственных
платоновым - это полуправильные выпуклые многогранники, или архимедовы тела. У
них все многогранные углы равны, все грани - правильные многоугольники, но
нескольких различных типов.
. Понятие многогранников
Само определение понятия многогранника
оказывается как раз таким вопросом, где необходимо особенно внимательно
сочетать наглядные представления, рассмотрение реальных примеров и логической
точности формулировок. Формулировки должны исходить из реальных примеров, из
наглядных представлений и возвращаться к ним для проверки и дальше - для
применения.
Выделяют два основных способа введения понятия
многогранника в школьном курсе стереометрии:
) многогранник как поверхность.
) многогранник как тело.
Чаще используется второй путь.
Дать строгое определение понятию многогранника в
школе трудно, так как в определение входят такие понятия как поверхность,
ограниченность, внутренние точки и др. Такая попытка была сделана в книге В.М.
Клопского, З.А. Скопеца, М.И. Ягодовского «Геометрия 9-10», но было очень
сложно, так как определение вводилось в несколько шагов, было много
вспомогательных понятий.
Наиболее целесообразно дать описание на основе
наглядных представлений школьника. Проще и короче всего определить многогранник
как тело, поверхность которого состоит из многоугольников (в конечном числе).
При этом «тело» и «поверхность» можно понимать в
наглядном смысле, как понимают обычно. Тело в отвлечении его от материальности
- это часть пространства. Поэтому данное определение можно пересказать и так:
многогранник - это часть пространства, ограниченная конечным числом
многоугольников.
Например, у Погорелова А.В.: «Многогранник - это
такое тело, поверхность которого состоит из конечного числа плоских
многоугольников»; У Атанасяна Л.С.: «Многогранник - это поверхность,
составленная из многоугольников и ограничивающая некоторое геометрическое тело»
[Погорелов А.В., 1990].
При этом в согласии с наглядным представлением
подразумевается следующее:
(1)Имеется в виду конечная часть пространства;
конечная в смысле конечности её размеров, или, как принято говорить в
математике, ограниченная. (Это оговаривается, поскольку можно считать, что
многоугольники, ограничивающие конечную часть пространства, ограничивают вместе
с нею и остальную его часть - бесконечную; во всяком случае, они тоже образуют
его границу.)
(2)Многоугольники, ограничивающие многогранник,
присоединяются к нему (содержаться в нем). Они образуют его поверхность;
остальная же часть многогранника - это его внутренность, так что многогранник
состоит из поверхности и внутренности.
(Это можно считать описательным определением
поверхности и внутренности.) Поверхность всюду прилегает к внутренности и
отделяет его от остального пространства - внешнего по отношению к
многограннику.
Поэтому, например, куб с «крылом», т.е. с
приложенным к нему прямоугольником со стороной на ребре куба, не считается
многогранником: крыло не прилегает к внутренности и никаким образом ее не
ограничивает, не отделяет от остального пространства.
(3)Многогранник, и даже одна его внутренность,
состоит из одного куска, или, как принято говорить в математике, связна: не
выходя из нее, можно непрерывно пройти от одной ее точки до любой другой. Или,
что в данном случае равносильно, любые две точки внутренности можно соединить
лежащей в ней ломаной.
Поэтому, например, два куба, приставленные один
к другому по ребру, т. е. имеющие общее ребро и ничего больше, не образуют
многогранника, а приставленные по куску грани - образуют его, так же как
объединение параллелепипеда с поставленным на него кубом и т. п.
Все сказанное содержится в наглядном
представлении о многограннике и явно оговаривается для того, чтобы
проанализировать это наглядное представление и тем самым выяснить, во-первых,
те его элементы, которые должны фигурировать в формально строгом определении
многогранника, а во-вторых, точнее различать в конкретных случаях, какая фигура
должна быть признана многогранником, а какая - нет.
)Дадим строгое определение многогранника,
предложенное А.Д. Александровым.
Начнем с кратких предварительных определений;
все они относятся как к пространству, так и к плоскости.
Фигура - это то же, что множество точек.
Точка называется граничной точкой данной фигуры,
если сколь угодно близко от нее есть точки, как принадлежащие фигуре, так и не
принадлежащие ей.
Точка фигуры, не являющаяся ее граничной точкой,
называется внутренней.
Множество всех граничных точек фигуры называется
ее границей, а множество всех ее внутренних точек - внутренностью [Александров
А.Д. 1981].
Замкнутой областью называется множество точек,
обладающее следующими свойствами:
(1)Оно содержит внутренние точки, а внутренность
его связна.
(2)Оно содержит свою границу, и она совпадает с
границей его внутренности.
Данное определение относится либо к множеству
точек на плоскости, либо - в пространстве. Замкнутая область в пространстве
называется телом, а на плоскости - плоской замкнутой областью или просто
замкнутой областью, если ясно, что речь идет о фигуре на плоскости.
Из определения замкнутой области - как на
плоскости, так и в пространстве - следует, что она состоит из внутренности и ее
границы, которая оказывается так же границей самой замкнутой области.
Поэтому замкнутую область можно определить
несколько иначе. Замкнутая область - это множество точек, имеющее (не пустую)
связную внутренность и состоящее из нее и ее границы.
Оба данные выше определения равносильны. Граница
замкнутой области всюду прилегает к ее внутренности. У «куба с крылом» «крыло»
входит в границу фигуры, но не содержится в границе ее внутренности. Граница
тела называется его поверхностью.
В определении замкнутой области не требуется,
чтобы она была ограниченной - имела конечные размеры; допускаются и бесконечные
области.
Примерами в пространстве могут служить
полупространство, двугранный угол, как множество, ограниченное двумя
полуплоскостями, и др. Все пространство тоже является телом - это единственное
тело, не имеющее границы.
Часто в само понятие тела включают требование
его ограниченности - конечности его размеров, но этого делать не будем, потому
что в геометрии имеют дело и с бесконечными телами. Точно так же и в
планиметрии встречаются и бесконечные области, например угол - часть плоскости,
ограниченная двумя лучами с общим началом.
Дадим теперь определение многоугольника и
многогранника.
Многоугольником называется замкнутая область
конечных размеров, граница которой состоит из конечного числа отрезков.
Многоугольник называется простым, если его граница представляет собой одну
простую замкнутую ломаную.
Многогранником называется тело конечных
размеров, граница (поверхность) которого состоит из конечного числа
многоугольников.
Данное определение повторяет определение на
основе наглядных представлений, однако теперь входящие в него понятия тела и
его поверхности понимаются не только наглядно, но и с точки зрения данных им
выше определений [Болтянский В.Г., 1966].
Нередко, как уже говорилось, многогранником
называют не тело, ограниченное многоугольниками, а поверхность, составленную из
многоугольников; такое словоупотребление встречается вне школьного курса даже
чаще. Встречается и смешение терминов, когда «многогранник» понимается то в
одном, то в другом смысле. Так, когда говорят, например, «склеим из развертки
куб», то имеют в виду не тело, а поверхность.
Подобное употребление одного и того же слова в
разных, хотя и тесно связанных, смыслах встречается в геометрии постоянно и,
можно даже сказать, характерно для нее.
Углом называют и фигуру, состоящую из двух
лучей, и ограниченную ею часть плоскости; так же как двугранный угол понимается
или как фигура из двух плоскостей, или как ограниченная ею часть пространства;
многоугольником называют и ломаную, и ограниченную ею часть плоскости, и т. п.
В этом нет ничего страшного, если каждый раз
понимать, в каком именно смысле употребляется в данный момент тот или иной
термин.
)Можно дать другое определение понятия
многогранника, если учесть следующее: фигура, составленная из многогранников,
прилегающих друг к другу по граням или по кускам граней, сама оказывается
многогранником, и так можно из простых многогранников составлять сколь угодно
сложные. Это замечание можно уточнить и получить из него новое определение
многогранника, исходя из самых простых многогранников - из тетраэдров. А именно
выполняется теорема.
Теорема. Всякое тело, составленное из
тетраэдров, является многогранником и всякий многогранник можно разбить на
тетраэдры или, что равносильно, составить из тетраэдров.
В несколько уточненной форме и не пользуясь
понятием тела, эту теорему можно высказать так:
Фигура является многогранником тогда и только
тогда, когда ее можно составить из конечного числа тетраэдров так, что:
(1)каждые два тетраэдра либо не имеют общих
точек, либо имеют только одну общую вершину, или одно общее ребро, или одну
общую грань;
(2)от каждого тетраэдра к каждому можно пройти
по тетраэдрам, последовательно прилегающим один к другому по целым граням.
Данная теорема позволяет определить многогранник
как фигуру, составленную из тетраэдров так, что выполнены условия (1), (2).
Такое определение, которое характеризует предмет
тем способом, каким он может быть построен, называется конструктивным.
Полученное определение многогранника именно такое; любой многогранник строится
последовательным прикладыванием тетраэдров по граням; а как строить тетраэдры -
известно.
В противоположность этому определения
многогранника, рассмотренные ранее, состоят в указании его характерных свойств
или, иначе говоря, в точном его описании. Такие определения называют
дескриптивными, т.е. описательными.
Описательное определение многогранника позволяет
судить о фигуре, является ли она многогранником или нет.
Посмотрел со всех сторон на данное тело, увидел,
что всюду его поверхность состоит из многоугольников, - значит, многогранник.
Такой же характер имеют, например, обычные определения призмы и пирамиды
[Глаголев Н.А. 1958].
Как и для многогранника, конструктивные
определения можно дать многоугольникам многогранной поверхности.
) Другой подход к определению многогранника
представлен в книге В.Г. Болтянского «Элементарная геометрия», построенный на
основе вейлевской векторной аксиоматики геометрии. Этот подход не применяется в
школьных учебниках, но для примера можно привести одно из определений.
При вейлевском изложении геометрии
первоначальными понятиями являются точка, вектор и следующие операции над ними:
паре точек сопоставляется некоторый вектор, сумма векторов, произведение
вектора на число и скалярное произведение, а также их свойства.
Наиболее известным примером многогранника
является параллелепипед. Его можно описать следующим образом. Берется
параллелограмм ABCD и из его вершин откладываются равные векторы АА1=ВВ1
=СС1 =DD1 =с, где с не параллелен плоскости
параллелограмма ABCD.
Определение частных видов многогранников
(призмы, пирамиды и др.) в данном подходе практически не отличаются от
определений в школьном курсе, однако интересен сам подход к определению на
основе другой аксиоматике.
Таким образом, определение многогранника может
быть дано различными способами, и в разной литературе и в разных учебниках
можно встретить различные подходы к определению.
Можно дать понятию многогранника как
дескриптивное, так и конструктивное определение, как определение, основанное на
наглядном представлении, так и строгое. Можно определить многогранник как тело
и как поверхность.
Различны также определения многогранника, данные
на основе различных аксиоматик. В школьных учебниках чаще дается какое-то одно
определение, но полезно учащимся показывать и другие способы определения
многогранника.
Как и при введении понятия многогранника,
существуют различные способы введения выпуклых многогранников и правильных
многогранников [Болтянский В.Г., 1966]. Рассмотрим эти способы подробнее.
После введения понятия многогранника в школе,
как правило, рассматривают выпуклые многогранники.
Удачным считается подход, когда сразу дается
определение выпуклого многогранника и для него определяются элементы, что
сделать легче. Изучение свойств как выпуклых многоугольников, так и выпуклых
многогранников занимает очень большое место в школьном курсе геометрии.
Однако точный смысл понятия «выпуклый» в средней
школе не раскрывается и причины, заставляющие требовать выпуклости
рассматриваемых многоугольников и многогранников, нигде не объясняются.
Учащиеся часто вообще не воспринимают смысла
прилагательного «выпуклый» и лишь по привычке, машинально в ответ на
предложение изобразить какой-либо четырехугольник рисуют фигуру.
При этом может показаться, что лишь недостаток
общей математической культуры заставляет их считать все четырехугольники
выпуклыми, подобно тому как наиболее слабые школьники иногда не в состоянии
представить себе четырехугольника, отличного от прямоугольника, параллелограмма
или, в лучшем случае, от трапеции.
В некоторых случаях игнорирование условия о
выпуклости многоугольника или многогранника оказывается даже совершенно
законным - какую, например, ценность имеет оговорка о выпуклости в теореме:
сумма углов выпуклого n-угольника равна (n - 2).180°
Условие этой теоремы полностью сохраняет силу и
для невыпуклых (простых) многоугольников; так, например, ясно, что сумма углов
и невыпуклого четырехугольника равна 360. Правда, приводимое в школе
доказательство теоремы справедливо лишь для выпуклых многоугольников.
Понятие выпуклого многогранника чаще всего
вводят по аналогии с выпуклым многоугольником. Очень хорошо эта аналогия
просматривается в учебнике Александрова. Существует два способа определения
выпуклого многогранника.
Многогранник называется выпуклым, если он лежит
по одну сторону от каждой из ограничивающих его плоскостей. Такой подход принят
в учебниках и. Либо многогранник называется выпуклым, если любые две его точки
могут быть соединены отрезком.
Такое определение дается в учебнике. В учебнике
за основу берется второе определение и доказывается возможность другого (в
нашем случае первого) определения [Каченовский М.И., 1959].
Остановимся подробнее на втором определении.
Чаще всего в геометрии рассматривают связные фигуры, т. е. такие, в которых
любые две точки можно соединить линией, целиком принадлежащей этой фигуре.
При этом соединяющая линия может оказаться
довольно сложной.
Естественно выделить класс фигур, для которых в
качестве линии, соединяющей две ее точки А, В, всегда можно выбрать самую
простую линию - прямолинейный отрезок АВ. Такие фигуры называются выпуклыми.
Фигура F называется выпуклой, если вместе с
каждыми двумя точками А, В она целиком содержит и весь отрезок АВ.
Кроме плоских, можно рассматривать
пространственные выпуклые фигуры (их обычно называют выпуклыми телами).
Примерами могут служить тетраэдр, параллелепипед, шар, шаровой слой и другие.
Выпуклые тела в пространстве можно определить
как пересечение некоторого множества полупространств. Простейшими выпуклыми
телами являются те, которые можно представить в виде пересечения конечного
числа полупространств. Такие выпуклые тела называются выпуклыми
многогранниками.
Свойство, положенное в основу определения
выпуклых фигур (существование в фигуре прямолинейного отрезка, соединяющего
любые две ее точки), с первого взгляда может показаться несущественными, даже
надуманным.
В действительности же выделяемый этим
определением класс выпуклых фигур является весьма интересным и важным для
геометрии. Дело в том, что «произвольные» геометрические фигуры могут быть
устроены необычайно сложно.
Например, определить, находится ли точка А
«внутри» или «вне» замкнутого многоугольника, совсем не просто. Если же рассматривать
фигуры, не являющиеся многоугольниками, то можно столкнуться и с гораздо
большими сложностями. Существует, например, плоская фигура, ограниченная не
пересекающей себя замкнутой линией и в то же время не имеющая ни площади, ни
периметра.
Для выпуклых фигур такие чудовищные явления не
могут иметь места: внутренняя область выпуклой фигуры сравнительно просто
устроена, любая ограниченная плоская выпуклая фигура обладает определенными
площадью и периметром, а пространственное выпуклое тело - объемом и площадью
поверхности и т. д. Таким образом, выпуклые фигуры составляют класс
сравнительно просто устроенных фигур, допускающих изучение геометрическими
методами [Зив Б.Г. 2000].
С другой стороны, класс выпуклых фигур является
достаточно обширным. Так, все фигуры и тела, рассматриваемые в элементарной
геометрии, либо являются выпуклыми, либо представляют собой несложные
комбинации выпуклых фигур и тел.
После введения выпуклых многогранников изучаются
их виды: призмы, пирамиды и их разновидности.
Практически во всех учебниках они определяются
одинаково. А при введении определения правильного многогранника авторы
учебников расходятся во взглядах.
Поэтому интересно рассмотреть различные подходы
к определению понятия правильного многогранника и их методические особенности.
В различных учебниках по стереометрии
используются разные определения этого понятия. Так, в учебнике и других
выпуклый многогранник называется правильным, если все его грани - равные
правильные многоугольники и, кроме того, в каждой вершине сходится одно и то же
число ребер.
В учебнике вместо условия равенства правильных
многоугольников требуется, чтобы правильные многоугольники были с одним и тем
же числом сторон. Пособие А.Д. Александрова и других по сравнению с учебником
накладывает дополнительное требование равенства всех двугранных углов
правильного многогранника. При этом многогранник называется выпуклым, если
любые две его точки соединимы в нем отрезком.
Учебное пособие дает такое определение: выпуклый
многогранник называется правильным, если все его грани - конгруэнтные
правильные многоугольники, и все его многогранные углы имеют одинаковое число
граней.
В многогранник называется правильным, если все
его грани - равные правильные многоугольники и все многогранные углы равны. И,
наконец, в книге сказано: многогранник называется правильным, если все его
грани -равные правильные многоугольники, и все его двугранные углы равны.
3. Свойства многогранников
Как видим, во всех перечисленных учебниках
даются различные определения понятия правильного многогранника, использующие
разные свойства правильных многогранников.
Перечислим их:
. Выпуклость многогранника.
. Все грани - равные правильные многоугольники.
. Все грани - правильные многоугольники с одним
и
тем же числом сторон.
. В каждой вершине сходится одинаковое число
ребер.
. Все многогранные углы имеют одинаковое число
граней.
. Равны все многогранные углы.
. Равны все двугранные углы.
Возможны и другие свойства правильных
многогранников, например:
. Равны все ребра многогранника.
. Равны все плоские углы многогранника.
Какие же свойства следует взять для определения
правильного многогранника? Каким методическим требованиям оно должно
удовлетворять?
Нам представляется, что для отбора свойств в
определении правильного многогранника нужно руководствоваться следующими
требованиями:
Всякое определение должно быть полным, т. е.
включать те свойства, которые полностью определяют данное понятие. Иными
словами, любое свойство данного понятия должно быть выводимо из свойств,
перечисленных в определении.
Всякое определение должно быть по возможности
экономным, т. е. не содержать лишних свойств, которые выводятся из остальных
свойств правильного многогранника.
Определение понятия правильного многогранника
должно отражать уже имеющиеся представления учащихся о слове
"правильный" (правильный многоугольник, правильная пирамида и т. д.).
Определение понятия правильного многогранника
должно быть пространственным аналогом определения понятия правильного
многоугольника на плоскости.
Определение правильного многогранника должно
допускать возможные обобщения, например, на случай полуправильных и
топологически правильных многогранников.
Определение должно быть педагогически
целесообразным, т. е. свойства, включенные в него, должны в той или иной
степени использоваться при изучении правильных многогранников, нести
определенные педагогические функции [Земляков А.Н., 1986].
Пространственными аналогами определения
правильного многоугольника являются определения, данные в пособиях.
К числу достоинств этих определений мы относим и
то, что в них отсутствует требование выпуклости, которое, с одной стороны,
является довольно сложным для учащихся, а с другой - фактически не используется
при доказательстве теорем и решении задач.
К недостаткам этих определений следует отнести
то, что они не обобщаются на случаи полуправильных и топологически правильных
многогранников. Например, равенство двугранных углов не переносится на случай
полуправильных многогранников.
Для определения топологически правильных
многогранников следует использовать свойства, носящие топологический характер.
Такими свойствами из перечисленных выше являются 3, 4 и 5. Поэтому лучше всего
для этих целей подходит определение правильных многогранников, данное в
учебнике.
Таким образом, мы видим, что ни одно из рассмотренных
выше определений правильного многогранника не является универсальным, т. е.
удовлетворяющим всем требованиям. В зависимости от целей обучения следует
выбирать и соответствующее им определение.
Так, если надо только ознакомить учащихся с
определением правильного многогранника, установив аналогию с определением
правильного многоугольника, не исследуя при этом подробно свойства правильных
многогранников, то целесообразно использовать определения, данные в пособиях.
Если же мы хотим рассмотреть свойства правильных многогранников более подробно,
в частности перейти к полуправильным и топологически правильным многогранникам,
то лучше всего обратиться к определениям из учебников.
II. Использование моделирования при
изучении темы «Многогранники»
. Геометрическое моделирование -
неотъемлемая часть современного математического образования
На практике часто приходится иметь дело с
реальными объектами, имеющими форму треугольника, прямоугольника, окружности и
так далее. На листе бумаги можно непосредственно с помощью линейки нарисовать
отрезок прямой и измерить его длину, с помощью циркуля нарисовать дугу
окружности и транспортиром измерить угловую величину этой дуги. Все это -
реальные операции над реальными объектами.
В геометрии эти реальные объекты и реальные
операции идеализируются, в результате чего получаются абстрактное понятие точки
как бесконечно малого по размерам следа от карандаша и абстрактное понятие
прямой как бесконечно тонкой линии, проведенной тем же карандашом с помощью
бесконечно длинной линейки. Эти абстрактные понятия являются геометрическими
моделями реальных объектов.
На реальном объекте можно провести эксперимент.
Например, на нарисованном треугольнике можно измерить линейкой и транспортиром
его стороны и углы и обнаружить, что против большей стороны лежит больший угол.
Возникает, таким образом, гипотеза, которая после се доказательства становится
теоремой и, следовательно, выполняется для любого достаточно точно построенного
реального треугольника [Зив Б.Г. 2000].
Аналогичный эксперимент провел в свое время Н.И.
Лобачевский. Он вычислил сумму внутренних углов треугольника, вершины которого
находятся соответственно на Солнце, Земле и Сириусе, и установил, что эта сумма
не более 180° и отличается от этого числа менее, чем на 0,000372".
Предположив, что эта сумма не равна все же 180°,
Н.И. Лобачевский и построил свою «воображаемую» геометрию, которая является
моделью той части реального пространства, где сумма внутренних углов
треугольника меньше 180°.
Исследования Н.И. Лобачевского привели к тому,
что аксиоматический метод стал основным в современной математике.
При аксиоматическом методе основные понятия
никак не определяются, а основные отношения определяются системой аксиом.
Поэтому в основные понятия может быть вложен
любой (допустимый) смысл, а в основные отношения - такой смысл, при котором
выполняются все аксиомы данной системы аксиом.
При этом получается модель рассматриваемой
аксиоматической теории. Слово «модель» здесь приобретает новое значение. С
одной стороны совокупность идеализированных объектов реального пространства
является моделью этого пространства, а с другой эта же совокупность является
(естественной) моделью аксиоматической теории евклидова пространства.
Если в основные понятия и отношения вложить
другой смысл, то получится другая модель этой же теории.
Обозначим, например, через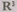 множество
всех троек действительных чисел. Тройку I,
множество
всех троек действительных чисел. Тройку I,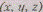 назовем «точкой», «расстоянием» между «точками»
назовем «точкой», «расстоянием» между «точками»  и
и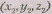 назовем
число
назовем
число
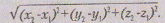
«Плоскостью» назовем четверку чисел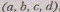 ,
определенную с точностью до отношения
,
определенную с точностью до отношения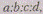 для
которой
для
которой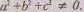 Если
теперь определить «принадлежность» «точки»
Если
теперь определить «принадлежность» «точки»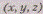 «плоскости»
«плоскости»
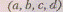 условием
условием
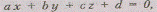
то множество станет
числовой моделью пространства.
станет
числовой моделью пространства.
Декартова прямоугольная система координат на
естественной модели пространства каждой точке М взаимно однозначно ставит в
соответствие тройку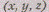 ее координат, то
есть «точку»
ее координат, то
есть «точку» 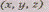 числовой модели
числовой модели 
На любой модели пространства можно ввести
декартову прямоугольную систему координат и этим взаимно однозначно с
сохранением основных отношений отобразить ее па числовую модель Это означает, что все модели пространства в определенном смысле одинаковы или,
как говорят, изоморфны.
Это означает, что все модели пространства в определенном смысле одинаковы или,
как говорят, изоморфны.
Другими словами, если некоторое предложение,
сформулированное в терминах основных понятий и основных отношений, выполняется
на одной из моделей, то оно выполняется и на всех других моделях.
Рисунок плоской геометрической фигуры,
выполненный на листе бумаги, является приближением естественной модели этой
фигуры с той степенью точности, которую позволяют использованные инструменты.
Обычные чертежные инструменты позволяют выполнять чертежи, степень точности
которых сравнима с точностью вычислений на логарифмической линейке.
Числовая модель пространства
построена в рамках теории действительных чисел. Аналогично можно строить модели
пространства в рамках планиметрии - плоскостные модели пространства.
пространства
построена в рамках теории действительных чисел. Аналогично можно строить модели
пространства в рамках планиметрии - плоскостные модели пространства.
Одна из таких моделей определяется методом Г.
Монжа (1746-1818), представление о котором дастся в школьных учебниках
геометрии [Киселев А.П., 1956]. Этот метод является основным в черчении. Иногда
его можно использовать при решении геометрических задач. Но чаше более
эффективными являются плоскостные модели пространства, построенные с помощью
других методов.
2. Федоровские модели пространства
Гениальный русский геометр и кристаллограф
Евграф Степанович Федоров (1853 -1919), занимаясь кристаллографией, искал
возможность геометрического моделирования кристаллических структур и с этой
целью построил две плоскостные модели пространства, одну из которых -
циклографическую - мы сейчас и рассмотрим.
Фиксируем в пространстве некоторую плоскость Н.
Она разбивает все пространство па два полупространства и
и .
Окружность в плоскости Н будем считать положительно ориентированной, если
определено движение точки по этой окружности так, что из любой точки
полупространства
.
Окружность в плоскости Н будем считать положительно ориентированной, если
определено движение точки по этой окружности так, что из любой точки
полупространства оно видно как
выполняющееся против часовой стрелки, и отрицательно ориентированной, если
движение по ней видно как выполняющееся против часовой стрелки из любой точки
полупространства Н". Положительно ориентированную окружность с центром в
точке А и радиуса
оно видно как
выполняющееся против часовой стрелки, и отрицательно ориентированной, если
движение по ней видно как выполняющееся против часовой стрелки из любой точки
полупространства Н". Положительно ориентированную окружность с центром в
точке А и радиуса будем обозначать
через
будем обозначать
через  ,
а отрицательно ориентированную - через
,
а отрицательно ориентированную - через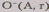 i.
Точки плоскости Н рассмотрим как окружности нулевого радиуса. Ориентированные
окружности и окружности нулевого радиуса называются циклами.
i.
Точки плоскости Н рассмотрим как окружности нулевого радиуса. Ориентированные
окружности и окружности нулевого радиуса называются циклами.
Определим теперь взаимно однозначное отображение
пространства на множество всех циклов плоскости Н по следующему правилу.
Обозначим через А ортогональную проекцию произвольной точки пространства на плоскость Н и через
пространства на плоскость Н и через -
длину отрезка
-
длину отрезка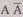
Поставим в соответствие точке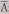 :
:
· окружность
нулевого радиуса с центром в точке А, если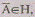
· цикл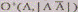 ,
если,
,
если,
· цикл ,если
(рис.
,если
(рис. 1).
1).
Построенное отображение переносит структуру
пространства на множество всех циклов плоскости Н, и это множество становится
(циклографической) моделью пространства. [Клопский В.М., 1979]
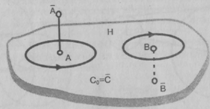
Рис. 1
На этой модели:
· прямая,
параллельная плоскости Н, изображается в виде множества всех одинаково
ориентированных циклов одного радиуса, центры которых лежат на одной прямой;
· прямая,
пересекающая плоскость Н, представляется как множество всех гомотетичных между
собой циклов с общим центром гомотетии, который является точкой пересечения
этой прямой с плоскостью Н;
· плоскость,
параллельная плоскости Н, изображается как множество всех одинаково
ориентированных циклов одного радиуса;
•плоскость, пересекающая плоскость Н по прямой d,
представляется как множество всех циклов, таких, что каждые два либо одинаково
ориентированы, имеют равные радиусы и прямая, проходящая через их центры,
параллельна прямой d, либо их
центр гомотетии лежит на прямой d,
и отношение радиусов этих циклов равно отношению расстояний от их центров до
прямой d [Люстерник Л.А.,
1956].
Расстояние между двумя «точками» на этой модели
пространства можно вычислить следующим образом. Рассмотрим, например, «точки»и.
На перпендикулярах к прямой АВ в точках А и В
по одну сторону
В
по одну сторону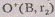 от прямой АВ
построим соответственно точки
от прямой АВ
построим соответственно точки и
и такие,
что
такие,
что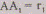 ,
,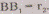 Длина
отрезка
Длина
отрезка  и
есть «расстояние» между рассматриваемыми «точками». Построенную выше
циклографическую модель пространства Е.С. Федоров применял для изображения
различных кристаллических структур. Например, структура, в которой атомы
расположены в вершинах куба, представлена на рис. 3.
и
есть «расстояние» между рассматриваемыми «точками». Построенную выше
циклографическую модель пространства Е.С. Федоров применял для изображения
различных кристаллических структур. Например, структура, в которой атомы
расположены в вершинах куба, представлена на рис. 3.
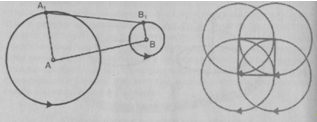
Рис. 2
Рис. 3
Замечательно, что каждой теореме стереометрии на
циклографической модели соответствуют несколько теорем о циклах на плоскости.
Рассмотрим, например, теорему: если точки А, В и С не принадлежат плоскости  и
не лежат на одной прямой, а прямые ЛВ, ВС и АС ее пересекают, то точки
пересечения этих прямых с плоскостью
и
не лежат на одной прямой, а прямые ЛВ, ВС и АС ее пересекают, то точки
пересечения этих прямых с плоскостью  лежат
на одной прямой. За «плоскость»
лежат
на одной прямой. За «плоскость»  на
циклографической модели примем «плоскость» Н. Приведенная теорема в терминах
планиметрии формулируется так: три центра гомотетии каждых двух из трех данных
ориентированных окружностей попарно различных радиусов лежат на одной прямой.
Принимая за «плоскость»
на
циклографической модели примем «плоскость» Н. Приведенная теорема в терминах
планиметрии формулируется так: три центра гомотетии каждых двух из трех данных
ориентированных окружностей попарно различных радиусов лежат на одной прямой.
Принимая за «плоскость»  другие
«плоскости», получим ещё несколько теорем планиметрии. Учитывая, кроме того,
существование других моделей пространства, Е.С. Федоров, подобно Архимеду,
говорил: «Дайте мне одну теорему и я создам множество теорем».
другие
«плоскости», получим ещё несколько теорем планиметрии. Учитывая, кроме того,
существование других моделей пространства, Е.С. Федоров, подобно Архимеду,
говорил: «Дайте мне одну теорему и я создам множество теорем».
От циклографической модели пространства легко
перейти к другой федоровской модели - векториальной.
Выберем на плоскости Н два взаимно
противоположных направления лучей и одно из них назовем положительным, а другое
- отрицательным. Поставим в соответствие каждому циклу пару точек 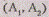 плоскости
Н так, что, если цикл является:
плоскости
Н так, что, если цикл является:
•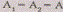 окружностью
нулевого радиуса с центром в точке А, то
окружностью
нулевого радиуса с центром в точке А, то
•окружностью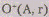 ,
то
,
то  »
а
»
а 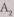 -
точка пересечения этой окружности с лучом положительного направления, имеющим
точку А начальной;
-
точка пересечения этой окружности с лучом положительного направления, имеющим
точку А начальной;
• окружностью 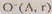 ,
то
,
то 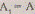 ,
а
,
а 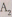 -
точка пересечения этой окружности с лучом отрицательного направления, имеющим
точку А начальной.
-
точка пересечения этой окружности с лучом отрицательного направления, имеющим
точку А начальной.
Построенное взаимно однозначное отображение
циклографической модели пространства на множество всех пар точек плоскости Н
переносит на это множество структуру пространства и оно тоже становится моделью
- федоровской векториальной моделью пространства.
Куб на этой модели пространства представлен на
рис. 4. Такое изображение куба достаточно наглядно и удобно для выполнения на
нем различных построений.
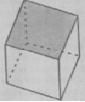
Рис.4
Далее, говоря «федоровская модель пространства»,
будем иметь в виду именно векториальную модель. Пока более подробно мы не будем
её рассматривать, поскольку она является лишь частным (хотя и очень важным)
случаем проекционнной модели евклидова пространства, являющейся предметом
нашего дальнейшего изучения.
3. Общие вопросы применения изображений
пространственных фигур в преподавании геометрии
Геометрия - составная часть математики, и
поэтому главные принципы ее преподавания вытекают из основных положений
обучения математики. «Математика является экспериментальной наукой - частью
теоретической физики и членом семейства естественных наук. Основные принципы
построения и преподавания всех этих паук применимы и к математике - считает
академик В.И. Арнольд. Первое из десяти основных положений, сформулированных
Л.Д. Кудрявцевым в его книге «Мысли о современной математике и её изучении»,
гласит: «В курсе математики изучаются математические модели». При таком
понимании сущности математики и её преподавания целями преподавания геометрии
являются:
· приобретение
учащимися знаний о свойствах реального пространства, геометрических фигур в нем
и (количественных и качественных) отношений между элементами этих фигур;
· приобретение
ими умений и навыков решения геометрических задач;
· развитие
теоретико-логического и образного мышления, их пространственного представления;
· приобщение
учащихся к исследовательской работе, проведению эксперимента;
· воспитание
интеллектуальных качеств личности, развитию которых способствуют занятия
математикой [Паповский В.М., 1993].
Очевидно, что преподавание геометрии немыслимо
без использования изображений, и вопрос лишь в том, как наиболее эффективно их
применять для достижения поставленных целей.
Предварительно уточним, что понимается под
изображением пространственной фигуры и какова его связь с моделью этой фигуры.
Начиная с работ К. Польке, под изображением пространственной фигуры обычно
понимают фигуру, подобную параллельной проекции оригинала па плоскость
изображений, то есть образ оригинала при аффинном отображении пространства на
плоскость изображений. Таким образом, изображение фигуры обязательно
предполагает наличие оригинала. А это значит, что приняв некоторую плоскость за
плоскость оснований и выбрав направление внутреннего проектирования, зная
оригинал и его изображение, всегда можно построить такую модель 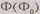 рассматриваемой
фигуры, в которой компонент Ф является ее изображением. При этом сама модель
рассматриваемой
фигуры, в которой компонент Ф является ее изображением. При этом сама модель 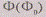 может
рассматриваться как оригинал. Например, если сказано, что квадрат ABCD
- изображение куба, то можно предполагать данной и федоровскую модель этого
куба с основанием
может
рассматриваться как оригинал. Например, если сказано, что квадрат ABCD
- изображение куба, то можно предполагать данной и федоровскую модель этого
куба с основанием 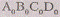 .
.
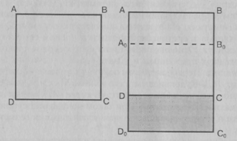
Рис. 5
Учитывая изложенное и не отождествляя понятия
изображения и модели, далее при упоминании об изображении, будем иметь в виду и
некоторую модель, связанную с ним.
Понятие изображения пространственной фигуры на
плоскости, определенное в терминах теоретико-логического мышления, является
вместе с тем и объектом образного мышления, и, поскольку речь идет об обучении,
средством воспитательного воздействия на учащихся. Отсюда вытекают следующие
свойства, которыми могут обладать или не обладать рассматриваемые изображения.
I. Верные
изображения. Это понятие введено Н.Ф. Четверухиным, и относится оно к
определенным выше изображениям. Дело в том, что в учебной литературе довольно
часто встречаются иллюстрации, выдаваемые за изображения, но не являющиеся
таковыми, если в слово «изображение» вкладывать его точный смысл. Подобные
иллюстрации Н.Ф. Четверухин назвал «неверными изображениями».
Изображения в широком смысле, используемые в
практической деятельности, очень разнообразны. Это и диаграммы, и схемы, и
карты, и чертежи, и произведения изобразительного искусства. Каждое из них
рассчитано на определенную область применения. Например, схема метро определяет
порядок следования станций на каждой линии, но не может служить для определения
расстояния между двумя станциями.
В каждом школьном учебнике геометрии приводится
определение изображения пространственной фигуры на плоскости. Учащийся вполне
естественно каждую иллюстрацию рассматривает как изображение. Поэтому неверные
изображения, как и неправильные аргументы в доказательстве теоремы, совершенно
недопустимы в преподавании геометрии, так как они препятствуют развитию
теоретико-логического мышления, создают неверное пространственное
представление, затрудняющее решение задач, и, возможно самое главное,
воспитывают такие черты характера, как небрежность и безответственность.
II. Наглядные
изображения. Изображение пространственной фигуры является наглядным, если оно
создаёт в воображении четкий пространственный образ оригинала. Формирование и
развитие образного мышления при обучении геометрии невозможно без использования
наглядных изображений. Однако когда образное мышление учащихся уже в
достаточной степени сформировано, вполне допустимо применять и не очень наглядные
изображения, такие, например, как федоровские модели фигур или выполненные по
методу Монжа представлено не наглядное изображение куба, но при обучении
решению задач уже достаточно подготовленных учащихся оно вполне может быть
использовано.
III. Изображения,
простые для выполнения. Таковыми являются изображения, для построения которых
требуются простые чертежные инструменты и небольшое число простых
конструктивных операций. Именно этими свойствами должны обладать изображения,
чтобы их можно было использовать во время учебных занятий при изучении теории и
при решении простейших задач. Простое для выполнения изображение можно быстро
построить, не отвлекая внимания учащихся от того основного, чему посвящено
занятие. Это не означает, что в преподавании геометрии применимы только простые
для выполнения изображения. Решение нетривиальных задач, исследовательская
работа, проведение экспериментов, организация самостоятельной работы учащихся
требуют использования иногда и довольно сложных для выполнения изображений.
Графический редактор CorelDRAW
6-8 позволяет строить такие изображения и размножать их в виде различных
печатных материалов, предназначенных для индивидуального использования
[Клопский В.М., 1979].
IV.Изображения,
простые для чтения. Изображения нужно уметь читать так же, как текст. И этому
умению учащихся необходимо обучать, начиная с изображений, простых для чтения.
Такие изображения должны быть оптимальных размеров, содержать немного
элементов, описывать лишь две или три конструктивные операции, причем
полученные; в результате каждой операции элементы должны быть четко выделены
при помощи различных изобразительных средств. Фактически разбивая сначала
сложные для чтения изображения на серию простых, нужно обучить учащихся делать
такое расчленение мысленно.
V. Функциональные
изображения. Это такие изображения, основным назначением которых является
эффективное решение поставленной геометрической задачи. Функциональность
изображения предполагает возможность наиболее просто выполнять на нем
необходимые дополнительные построения и на этой основе строить схему или
гипотезу решения задачи. Функциональные изображения не всегда бывают
наглядными, но без их использования невозможно полноценное обучение решению
геометрических задач. Довольно часто роль функциональных изображений выполняют
федоровские модели пространственных фигур.
VI.
Изображения, достаточно точно построенные. Назначением таких изображений
является проведение исследований, экспериментов и приближенных вычислений.
Достаточно точно построенные изображения, выполненные на бумаге с помощью
чертежных инструментов, можно использовать для приближенных вычислений с
точностью до двух значащих цифр, а выполненные на дисплее компьютера, - с
точностью до пяти значащих цифр. Эти изображения являются таким же средством
вычислений, как аналоговые вычислительные машины, только с меньшей степенью
точности, а проводимые на них математические эксперименты но своей
достоверности равносильны физическим экспериментам. Применение в преподавании
геометрии достаточно точно построенных изображений позволяет избежать
формализма и приобщить учащихся к математическому моделированию.
VII.
Композиционное изображение. Это понятие введено художником П.Я. Павлиновым и
относится оно к изображениям, выполненным в соответствии с правилами
художественной композиции. Эти изображения воспитывают художественный вкус,
благоприятны для зрительного восприятия и таким образом поддерживают интерес к
изучению геометрии.
Рассмотренные свойства изображений следует
использовать в зависимости от вида учебного процесса.
4. Изображения в систематическом
курсе геометрии. Типичные ошибки
Изложение курса геометрии в учебнике или во
время учебных занятий (на лекциях или уроках) предполагает наличие определенной
системы учебного материала. Понятно, что и изображения пространственных фигур
должны быть систематизированы, то есть, должна быть предусмотрена определенная
связь последующих изображений с предыдущими. Без такой систематизации
изображений невозможно добиться ни полноценного усвоения учащимися
геометрических знаний, ни должного уровня развития их образного мышления.
Основой развития образного мышления является
графическая грамотность. П.Я. Павлинов приводит слова Дидро: «Страна, в которой
учили бы рисовать так же, как учат читать и писать, превзошла бы вскоре все
остальные страны во всех искусствах, науках и мастерствах и, тоже проводя
параллель между обучением письму и обучением графической грамотности, считает,
что «количество различных примеров должно перейти в качество свободного умения
изображать всякую вещь». И далее: «Это умение должно проникнуть в подсознание,
подобно тому, как при обучении письму мы сначала изучаем графическое
изображение букв (А, Б, В и т. д.) и эти изображения являются на данном этапе
самодовлеющими. Но проходит время, и из этих букв составляются слова. Форма
буквы для буквы начинает ослабляться, её начинает замещать форма буквы в слове,
связь буквы с мыслью, и, наконец, из нашего сознания эта форма исчезает, уходит
в подсознание, вместо этого появляется непосредственное умение писать знаками
свою мысль, звуковое сочетание» [Саакян С.М., 2000].
Обучение графической грамотности и на ее основе
развитие образного мышления диктует следующие принципы системы изображений в
курсе геометрии:
· каждое
изображение системы должно обладать свойствами, в наибольшей степени
способствующими достижению целей преподавания геометрии;
· изображений
должно быть достаточно много;
· должны
использоваться различные изображения одной и той же фигуры;
· сложные
для построения и их чтения изображения должны складываться из сочетающихся с
ними предшествующих простых, выполненных на одной и той же проекционной модели
пространства.
Покажем применение этих принципов на примерах
изображений основных фигур в курсе геометрии.
Плоскость. На рис. 6 приведены восемь
изображений куска горизонтальной плоскости (плоскости оснований). В учебнике
А.В. Погорелова читаем: «Плоскость мы представляем себе как ровную поверхность
крышки стола... и поэтому будем изображать ее в виде параллелограмма». Учащиеся
повседневно имеют дело со столами, с их крышками в виде прямоугольника, и
поэтому изображение а) (рис. 6) куска плоскости подсознательно ассоциируется у
них с изображением прямоугольника. Поэтому применение только таких изображений
плоскости неизбежно приводит к ошибкам, о чем далее еще будет идти речь.
Куб. Ранее рассматривались изображения куба в
связи с решением задач на построение моделей фигур. Теперь же рассмотрим
изображение куба как один из основных элементов системы изображений курса
геометрии.
Здесь наиболее значительная роль изображений
куба состоит в том, что на их основе строятся изображения декартовой
прямоугольной системы координат. Изображению куба во фронтальной диметрии (рис.
6, а) соответствует изображение декартовой прямоугольной системы координат в
кабинетной проекции (рис. 7, а), федоровской модели куба (рис. 6, б) -
изображение декартовой прямоугольной системы координат в военной проекции (рис.
7, б), ортогональной проекционной модели куба (рис. 6, в) - изображение
декартовой прямоугольной системы координат в ортогональной проекции (рис. 7,
в). Если изображение декартовой прямоугольной системы координат в кабинетной
или военной проекции строится просто, то этого нельзя сказать об ортогональной
проекции.
При решении задач на комбинации куба и сферы
можно сначала построить изображение сферы в ортогональных проекциях и только
потом изображение куба. При изучении же уравнения сферы или другой поверхности
вращения в курсе геометрии преподаватель вынужден сначала построить изображение
декартовой прямоугольной системы координат в ортогональных проекциях и только
потом изображение изучаемой поверхности [Погорелов А.В., 1990].
Рассмотрим прямой трехгранный угол О'х'уУ и
плоскость изображений, пересекающую этот угол по треугольнику ЛВС (рис. 8).
В тетраэдре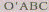 противоположные
ребра перпендикулярны.
противоположные
ребра перпендикулярны.
Поэтому ортогональная проекция О точки на
плоскость ABC является
ортоцентром треугольника ABC.
Основания высот треугольника ABC
принадлежат его сторонам, так как являются также основаниями высот, проведенных
через вершину О' в прямоугольных треугольниках
на
плоскость ABC является
ортоцентром треугольника ABC.
Основания высот треугольника ABC
принадлежат его сторонам, так как являются также основаниями высот, проведенных
через вершину О' в прямоугольных треугольниках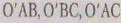 .
Поэтому треугольник ABC
-остроугольный, а ортогональные проекции
.
Поэтому треугольник ABC
-остроугольный, а ортогональные проекции ребер
данного прямого трехгранного угла, принадлежат прямым, содержащим высоты этого
треугольника. Нетрудно доказать, что и наоборот: прямые, содержащие высоты
любого остроугольного треугольника на плоскости изображений, содержат
ортогональные проекции ребер некоторого прямого трехгранного угла.
ребер
данного прямого трехгранного угла, принадлежат прямым, содержащим высоты этого
треугольника. Нетрудно доказать, что и наоборот: прямые, содержащие высоты
любого остроугольного треугольника на плоскости изображений, содержат
ортогональные проекции ребер некоторого прямого трехгранного угла.
Приходим, таким образом, к следующему построению
изображения декартовой прямоугольной системы координат (а следовательно, и
куба) в ортогональных проекциях. Строим на плоскости изображений остроугольный
треугольник ABC и его
ортоцентр О. Прямые ОА, ОВ, ОС и являются изображениями осей декартовой
прямоугольной системы координат в ортогональных проекциях. Построение
изображений единичных отрезков на осях координат и куба в ортогональных
проекциях показано на рис. 9.
При определенном уровне развития образного
мышления построение остроугольного треугольника и его высот может быть
воображаемым.
Цилиндр. Отметим только наиболее значимые в
курсе геометрии изображения цилиндра. На рис. 10 для определенности приведены
изображения одного и того же цилиндра с квадратным осевым сечением, причем
изображения а) и б) выполнены соответственно в полуортогональной и косоугольной
диметрии, а изображение б) - в ортогональных проекциях. Поэтому на изображениях
а) и б) осевое сечение цилиндра представлено в натуральную величину, а на
изображении в) - прямоугольником.
Конус. При построении изображения конуса
необходимо обратить внимание учащихся на то, что две контурные образующие
конуса не могут совпадать с его двумя фронтальными образующими. На рис. 11
представлены изображения а) и б) конуса соответственно в полуортогональной и
косоугольной диметрии, причем изображение б) выполнено так, что одна из
контурных образующих конуса совпадает с одной из фронтальных.
Сфера. Как и в случае цилиндра на рис. 12
представлены изображения а) и б) сферы соответственно в полуортогональной и
косоугольной фронтальной диметрии и изображение в) в ортогональных проекциях.
На изображении а) главный меридиан сферы представлен окружностью, а на
изображении в) - эллипсом.
Рассмотрим теперь типичные ошибки в изображениях
пространственных, возникающие как правило в результате игнорирования основных
принципов построения системы изображений в курсе геометрии. В учебниках А.В.
Погорелова и Л.С. Атанасяна и др. горизонтальная плоскость изображается
единственным образом так, как на рис. 1 ,а, и для цилиндра, конуса и сферы тоже
приняты только такие изображения, как на рис. 10, а, 11, а и 12, в
соответственно. Объединяя изображение плоскости с изображениями цилиндра, конуса
и сферы, учащиеся естественно получат изображения, представленные на рис.
13-16.
Эти изображения неверны, так как на каждом из
них направления сторон параллелограмма, представляющего прямоугольник, не
сопряжены относительно эллипса, представляющего окружность. На этих
изображениях и далее знак означает, что соответствующее изображение неверно.
Соответствующие верные изображения представлены
на рис. 16-19.
Использование в систематическом курсе геометрии
изображений, подобных представленным на рис. 12 - 15, только на первые взгляд
может показаться допустимым. Дело в том, что оно порождает устойчивое неверное
пространственное представление.
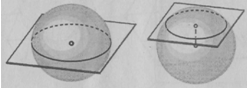
Рис.15 Рис. 16
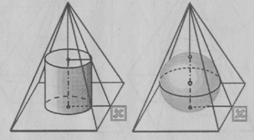
Рис.17 Рис.18
Человек, воспринявший это представление, будет
изображать цилиндр и сферу, вписанные в правильную четырехугольную пирамиду так
же, как на рис. 17 и 18, тогда как верные изображения в ортогональных проекциях
представлены на рис. 19 и 20, а в косоугольной фронтальной диметрии - на рис.
21 и 22.
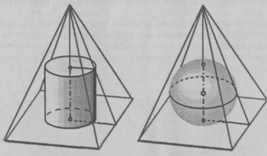
Рис. 19 Рис. 20
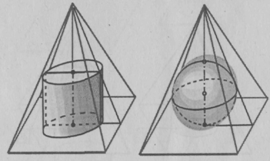
Рис. 21 Рис. 22
Другим примером, когда использование
однообразных изображений геометрических фигур приводит к возникновению неверных
пространственных представлений, служат комбинации сферы с кубом и декартовой
прямоугольной системы координат. Часто в учебниках куб и декартову
прямоугольную систему координат изображают только в кабинетной проекции, а
сферу - только в ортогональных проекциях. Совмещая эти изображения, получают
неверные изображения, представленные на рис. 23 и 24. Соответствующие верные
изображения в кабинетной проекции приведены па рис. 25 и 26, а в ортогональных
проекциях - на рис. 27 и 28.
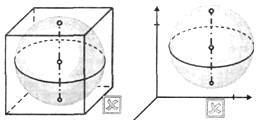
Рис. 23 Рис. 24
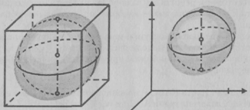
Рис. 25 Рис. 26
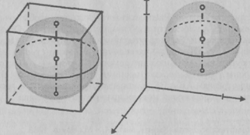
Рис.27 Рис.28
Роль изображений при решении геометрических
задач
При изучении теории курса геометрии доминирующую
роль играют такие свойства изображений, как наглядность, простота выполнения и
чтения изображения. При решении геометрических задач на первое место выходит
функциональность изображения, позволяющая понять суть решаемой проблемы.
В лекции «О профессии математика» академик А.Н.
Колмогоров приводит такой пример: «В задаче: В куб вложено два правильных
тетраэдра так, что четыре вершины куба служат вершинами одного из них, а
остальные четыре вершины куба - вершинами другого. Какую долю куба составляет
объем общей части этих тетраэдров? вся трудность заключается в том, чтобы
наглядно понять, что за фигура получается при пересечении тетраэдров».
Опыт педагогической работы и эксперименты
показывают, что 90% учащихся, построивших верное, наглядное и функциональное
изображение рассматриваемой в задаче пространственной фигуры, в состоянии
решить эту задачу. И учащихся необходимо приобщать к построению таких
изображений, показывая образцы их выполнения.
Очень часто наиболее функциональными
изображениями оказываются федоровские модели фигур. Поэтому именно на примере
их использования и покажем применение изображений при решении задач.
Задача1. Пусть РАВС - правильный тетраэдр, PQ
- его высота. Точка X лежит на
грани АРС, точка Y - на ребре
РВ, Z - па ребре АВ. В
каких границах лежит угол, который составляют с высотой PQ
прямые: а) ВХ; б) YZ
?
Построение модели. Расположим тетраэдр так,
чтобы точки А, В, С находились в плоскости изображений, а точки В, Р, Q
во фронтальной плоскости. Тогда треугольники ABC
и BPQ будут представлены
на модели в натуральную величину. Поэтому строим правильный треугольник ABC,
находим середину Е стороны АС, на отрезке BE
строим треугольник со сторонами ВР и ЕР, равными соответственно отрезкам АВ и BE,
и, проведя отрезки АР и СР, завершим построение федоровской модели правильного
тетраэдра.
Решение.
а)Выберем точку X
на грани АРС и построим се основание Хо (рис. 149). Угол Z.BXX0
- угол между прямыми ВХ и PQ.
Определим его натуральную величину, повернув треугольник ВХХ0
относительно перпендикуляра в точке В к плоскости ABC
до совмещения его плоскости с плоскостью РВЕ. Для этого через точку Хп
проведем окружность с центром в точке В, найдем ее точку пересечения Х'ос
лучом BE и на
перпендикуляре к прямой BE
в точке Х'п по одну сторону с точкой Р от прямой BE
отложим отрезок Х'0Х'» равный отрезку Х0Х. Прямая ВХ'
пересекает отрезок PQ
в точке R. Угол Z.BRQ
равен рассматриваемому, а его величина как величина внешнего угла треугольника BPR
не меньше величины угла L
BRQ и не больше 90°.
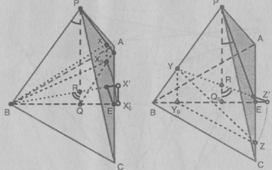
Рис.29 Рис.30
б)Выберем точку Y
на ребре ВР, точку Z- на ребре
АС и построим основание Yo
точки Y (рис. 150). Угол
/_ZYY0
и есть угол между прямыми YZ
и PQ. Определим его
натуральную величину, повернув треугольник YY()Z
вокруг прямой YY0
до совмещения его плоскости с плоскостью РВЕ. Для этого через точку Z
проведем окружность с центром в точке Yo
и найдем ее точку пересечения Z'
с лучом YQE.
Прямая YZ' пересекает
отрезок PQ в точке R.
Угол LQRZ' равен
рассматриваемому, а его величина как величина внешнего угла треугольника PRF
не меньше величины угла Z.QPE
и не больше 90°.
Задача 2. Точка D
- середина ребра правильной
треугольной призмы
правильной
треугольной призмы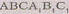 . Правильная
треугольная пирамида SMNP
расположена так, что се основание MNP
лежит в плоскости ABC,
точка М лежит на продолжении отрезка АС, причем
. Правильная
треугольная пирамида SMNP
расположена так, что се основание MNP
лежит в плоскости ABC,
точка М лежит на продолжении отрезка АС, причем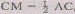 ребро SM проходит
через точку D, а ребро SP
пересекает отрезок ВВ, в точке К. В каком отношении отрезок ВВ[
делится точкой К?
ребро SM проходит
через точку D, а ребро SP
пересекает отрезок ВВ, в точке К. В каком отношении отрезок ВВ[
делится точкой К?
Построение модели. Построим сначала федоровскую
модель призмы АВСАС,. Затем построим середину Е отрезка АС и точку М,
удовлетворяющую условию задачи. Из точки О - основания высоты пирамиды - отрезки
BE и ME
видны под углом 120°. Поэтому точку О строим как пересечение двух дуг
окружностей с угловой величиной 120°, стягивающих соответственно отрезки ME
и BE (рис. 31).
Основание MNP
пирамиды можно построить как правильный треугольник, вписанный в окружность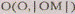 \,
а ее вершину S -как точку
пересечения прямой DN
с прямой, проходящей через точку О параллельно боковым ребрам призмы. Теперь
нетрудно построить точку К, точку
\,
а ее вершину S -как точку
пересечения прямой DN
с прямой, проходящей через точку О параллельно боковым ребрам призмы. Теперь
нетрудно построить точку К, точку пересечения
ребра SP с
основанием
пересечения
ребра SP с
основанием и основание L
точки
и основание L
точки (рис.
32).
(рис.
32).
Анализ модели. Из подобия треугольников КРВ и КLВ,
находим KB
KPBP ОМ-ОВ KB,
KL BL
ОВ-ОЕ
Задача сводится, таким образом, к определению длин
отрезков ОЕ, ОВ, ОМ. Решение. Положим АВ = а и обозначим через Q
и R центры дуг
окружностей, при пересечении которых получается точка О (рис. 151). Прямая QR
пересекает отрезок АК в точке F
и отрезок BE в точке G.
Точка R является серединой
отрезка АВ, с основанием Н перпендикуляра, опущенного из точки R
на прямую АС, - серединой отрезка АЕ. Так как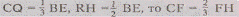 и
из равенства
и
из равенства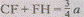 следует, что '
следует, что '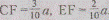 ,
Кроме того, так как
,
Кроме того, так как 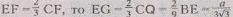 и по теореме
Пифагора
и по теореме
Пифагора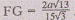 Таким образом,
Таким образом,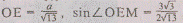
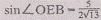 и
и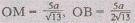
Подставляя в равенство найденные значения длин
отрезков ОЕ, ОМ и ОВ, находим, что искомое отношение равно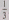 .
.
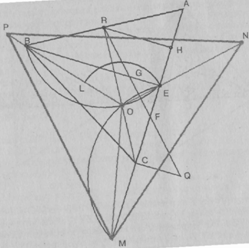
Рис. 31
Задача 65. Куб поворачивается, проходящей через
середины двух параллельных ребер, не принадлежащих одной грани. Каким должен
быть угол поворота, чтобы объем пересечения данного куба с повернутым составлял
бы объема данного куба?
Построение модели.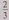 Диагональная
плоскость куба, перпендикулярная оси вращения, является плоскостью симметрии,
как данного куба, так и повернутого. Поэтому достаточно рассмотреть вращение
только половины куба, отсекаемой диагональной плоскостью, Модель объединения
половины данного куба и половины повернутого получается в результате применения
решения задачи 30. В зависимости от значения
Диагональная
плоскость куба, перпендикулярная оси вращения, является плоскостью симметрии,
как данного куба, так и повернутого. Поэтому достаточно рассмотреть вращение
только половины куба, отсекаемой диагональной плоскостью, Модель объединения
половины данного куба и половины повернутого получается в результате применения
решения задачи 30. В зависимости от значения угла поворота
возможны два случая, представленные соответственно на рис. 33 и 34:
угла поворота
возможны два случая, представленные соответственно на рис. 33 и 34:

Рис. 32
) Анализ модели. Менее наглядное, но более
функциональное по сравнению с рис. 33 соответствующее изображение представлено
на рис. 35. Анализируя его, находим, что плоскости ОХР, OPZ
и OXZ разбивают
пересечение рассматриваемых полукубов на четыре равных многогранника, один из
которых есть KPOXYZ. Последний
же многогранник плоскостью КОХ разбивается на четырехугольную пирамиду KOXYZ
и тетраэдр КОРХ, равновеликий тетраэдру ZOPX.
В рассматриваемом случае задача, таким образом, сводится к вычислению площадей
треугольников OXZ и XYZ.
2) Анализ модели. Как и в первом случае заменим изображение на рис. 34, более
функциональным, представленным на рис. 36.
Рис. 33 Рис. 34
Рис.35
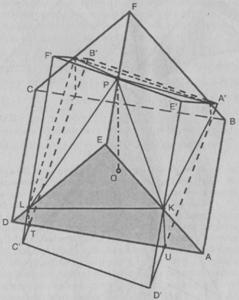
Рис. 36
Заметим, что в этом случае пересечение двух
полукубов получится, если от одного полукуба отсечь два тетраэдра, равных
тетраэдру EKLP, и две
усеченные пирамиды, равных пирамиде KUD'LNC'.
Поэтому для вычисления объема пересечения двух полукубов достаточно вычислить
длины отрезков DT
и U А.
Решение. Обозначим через а длину ребра данного
куба и через V его объем. В
первом случае (рис. 37) имеем и, если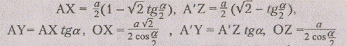 S-
площадь четырехугольника OXYZ,
S-
площадь четырехугольника OXYZ,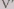 ""
- объем пересечения рассматриваемых
""
- объем пересечения рассматриваемых кубов,
или
кубов,
или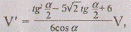 то есть в этом случае
то есть в этом случае
Во втором случае (рис.158), положив AU=
p, DT=<,
находим
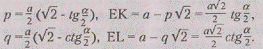
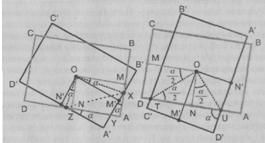
Рис.37 Рис.38
Обозначив через объем
тетраэдра EKLP и через
объем
тетраэдра EKLP и через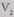 объем
пирамиды
объем
пирамиды ,получаем
,получаем
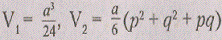
Таким образом, объем пересечения данного и
повернутого кубов равен
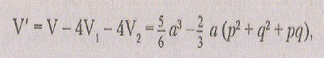
Или
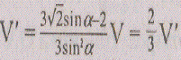
Решая уравнение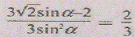 находим, что искомое значение
находим, что искомое значение равно 45°.
равно 45°.
Во всех трех рассмотренных задачах построенные
изображения помогают найти схему решения задачи и кратко записать ее решение.
Выбор изображения или системы изображений определяется условием задачи и ходом
ее решения.
В задаче 63 нахождение угла между двумя прямыми,
одна из которых содержит высоту правильного тетраэдра, предполагает вращение
другой прямой вокруг прямой, перпендикулярной плоскости основания тетраэдра.
Это и определило выбор изображения в пользу федоровской модели.
Решение задачи 2 связано с построением основания
высоты пирамиды и последующим построением пересечения пирамиды и призмы. Здесь
федоровская модель пространства использована потому, что на ней евклидова
структура горизонтальной плоскости совпадает со структурой плоскости
изображений (основания призмы и пирамиды изображены в натуральную величину).
Чтобы изображение было простым для чтения, оно разбито на два.
Из условия задачи 3 (данный и повернутый кубы
имеют общую плоскость симметрии, перпендикулярную оси вращения) следует, что
вместо кубов можно рассматривать соответствующие полукубы, а наличие вращения
снова вынуждает отдать предпочтение федоровской модели. Использование по три
изображения для каждого случая обусловлено тем, что функции этих изображений
различны.
И.Ф. Шарыгин считает, «что пространственные тела
можно разделить на две группы: -«хорошие», удобные для изображения, и «плохие»».
И далее: «К первой группе относятся треугольные призмы (в первую очередь
правильные), параллелепипеды, треугольные и четырехугольные пирамиды. Ко второй
- и-угольные (я>4) призмы и пирамиды, усеченные пирамиды и круглые тела,
особенно сфера.
Один из весьма распространенных приемов состоит
в том, что в заданной «неудобной» конструкции вычленяется в качестве ключевого
элемента «хороший» многогранник».
С высказанными положениями согласиться довольно
трудно. К задаче: На плоскости лежат четыре шара радиуса R,
причем три из лих попарно касаются друг, друга, а четвертый касается двух из
них. На эти шары положены сверху два шара меньшего радиуса, касающиеся друг
друга, причем каждый из них касается трех больших шаров. Найдите радиус
маленьких шаров - не надо строить изображение шести шаров не потому, что шар -
«плохая» фигура, а потому, что задача к шарам имеет лишь формальное отношение.
По сути, задача относится лишь к системе точек, состоящей из центров шаров и
точек их касания. В задачах же, относящихся к сферическим треугольникам
(особенно в небесной механике), изображения сферы и сферических треугольников
на ней совершенно необходимы и приобщать учащихся к этим изображениям можно и
нужно на примерах именно вписанных и описанных около многогранников сфер. Построение
таких изображений развивает пространственное представление и воспитывает
графическую грамотность учащихся. По мнению П.Я. Павлинова, «каждый может
научиться рисовать». И еще: «Время всеобщей графической грамотности неизбежно
придет. Недопустимо ожидать, чтобы само собой появилось умение грамотно
рисовать. За овладение графической грамотностью надо взяться сейчас же, не
задерживаясь».
III. Методические аспекты изложения
темы «Многогранники» в школьном курсе
. Обзор изложения темы
«Многогранники» в учебниках разных авторов
В школьных учебниках после изучения
«бесконечно-протяженных» и в силу этого весьма абстрактных геометрических
фигур: прямых и плоскостей (вернее сказать, их взаимного расположения в
пространстве) изучаются зримые, «конечные», даже, можно сказать, осязаемые
пространственные фигуры, и в первую очередь многогранники. Многогранник
(точнее, модель многогранника) можно изготовить, повертеть в руках,
«развернуть» его поверхность или даже «разрезать» - посмотреть на сечение. В
данной теме это весьма существенно, и учителю необходимо использовать
значительно расширившиеся возможности привлечения наглядности, наглядных
средств (не забывая уделять достаточное внимание и построению проекционных
чертежей). О наглядных средствах поговорим немного позднее.
Можно указать на такие две проводимые
методологические линии в изучении геометрии многогранников: это их
классификация и изучение различного рода количественных характеристик. Конечно,
эти линии переплетаются между собой. В данной теме рассматриваются простые
характеристики - численные: длины ребер, высоты, величины углов, площади
поверхностей, - и качественные, типа «правильности». Собственно говоря,
качественные характеристики - это одна из основ классификации многогранников.
Если исключить стоящие чуть в стороне от ведущей линии курса правильные
многогранники (пять «платоновых тел»), то логическую схему классификации
«школьных» многогранников можно описать примерно следующим образом.
Рассматриваются (и строго определяются) только два вида многогранников: призмы
и пирамиды. Конечно, внутри этих видов проводится грубая классификация по числу
углов - призмы и пирамиды бывают n-угольными, где n = 3, 4, 5,…. Более
детальная классификация - по взаимному расположению ребер и граней, по виду
граней. Для призм она относительно «разветвленная».
Школьная классификация пирамид менее
разветвленная:
Первая задача учителя - добиться от всех
учащихся знания этой классификации в том виде, в каком она подается в учебном
пособии, т. е. в виде соответствующих определений. И у ученика, и у учителя при
изучении данной темы может возникнуть вполне естественный вопрос: почему
столько внимания (и столько задач) посвящается всего лишь трем частным типам
многогранников - параллелепипедам, правильным призмам и правильным пирамидам?
Причин по крайней мере три: 1) эти многогранники нужны для дальнейшего
построения теории (главным образом теории объемов); 2) они обладают симметрией,
как многие формы природы и творения рук человеческих (скажем, архитектурные
формы); 3) они обладают «хорошими свойствами», т. е. для них можно
сформулировать и доказать достаточно простые теоремы.
Последнее преимущество обусловлено свойствами
симметричности; с другой стороны, как раз «хорошие свойства» и используются в
теоретических целях. Все теоремы этой темы относятся к «избранным»
многогранникам, причем, совсем, просто доказываются и наполовину имеют
вычислительный характер (т. е. вид формул). Поэтому вторая задача учителя -
добиться знания учащимися всех теорем (с доказательствами).
Третья по счету, но первоочередная для учителя
задача - научить школьников решать задачи. Практически все задачи (упражнения)
темы вычислительные, большую часть из них составляют простые или совсем простые
задачи, и здесь перед учителем раскрываются большие возможности в продолжение
линии обучения школьников эвристическим приемам решения задач. В задачах
находят отражение и главные методологические идеи решения задач - аналогия
стереометрии с планиметрией, сведение стереометрических задач к
планиметрическим.
Рассмотрим изучение темы «Многогранники» в
школьных учебниках. Для примера возьмем учебники разного уровня изложения
материала: предназначенные для общеобразовательной школы, для гуманитарных
классов, для классов с математическим уклоном.
Рассмотрим изучение темы «Многогранники» по
учебнику Атанасяна. Этот учебник предназначен для общеобразовательной школы.
Остановимся на нем подробнее.
Данная тема изучается в главе. На изучение ее
отводится 12 уроков. Ниже приведено поурочное планирование в таблице.
|
Номер
урока
|
Содержание
учебного материала
|
§1.
Понятие многогранника. Призма. Понятие многогранника. Призма. Площадь
поверхности призмы. ( п.25-27)
|
|
|
5-9
|
§2.
Пирамида. Пирамида. Правильная пирамида. Усеченная пирамида. Площадь
поверхности пирамиды. (п.28-30)
|
|
|
10
|
§3.
Правильные многогранники. Симметрия в пространстве. Понятие правильного
многогранника. Элементы симметрии правильных многогранников. (п. 31-33)
|
|
|
11
|
Контрольная
работа.
|
|
|
12
|
Зачет
по теме.
|
|
Еще до изучения темы «Многогранники» учащиеся
знакомятся с их простейшими видами в главе 1 §4 «Тетраэдр и параллелепипед». На
их изучение отводится 5 часов. Понятия тетраэдра и параллелепипеда вводятся в
данной главе для того, чтобы рассмотрение их свойств, построение сечений
способствовали углублению понимания вопросов взаимного расположения прямых и
плоскостей, поэтому необходимо, чтобы решение задач сопровождалось ссылками на
аксиомы, определения и теоремы.
При объяснении понятий тетраэдра и
параллелепипеда необходимо подчеркнуть, что многоугольник в пространстве
представляет собой плоскую поверхность, а тетраэдр и параллелепипед -
поверхности, составленные из плоских поверхностей (многоугольников).
Для формирования у учащихся представления о
способах изображения на чертеже тетраэдра и параллелепипеда полезно с помощью
диапроектора показать на экране различные проекции их каркасных моделей.
Полезно также обсудить простейшие свойства параллельной проекции.
В результате изучения параграфа учащиеся должны
уметь объяснить, что называется тетраэдром, параллелепипедом, указывать и
называть на моделях и чертежах элементы этих многогранников; знать свойства
граней и диагоналей параллелепипеда; уметь изображать тетраэдр и
параллелепипед, строить их сечения.
Основная цель темы «Многогранники» - дать
учащимся систематические сведения об основных видах многогранников.
Учащиеся уже знакомы с такими понятиями, как
тетраэдр и параллелепипед, и теперь им предстоит расширить представления о
многогранниках и их свойствах. В учебнике нет строгого математического
определения многогранника, а приводится лишь некоторое описание, так как
строгое определение громоздко и трудно не только для понимания учащимися, но и
для его применения. Такое наглядное представление о геометрических телах вполне
достаточно для ученика на первичном уровне рассмотрения понятия. Ниже, в п. 26,
рассматривается определение геометрического тела, в связи, с чем вводится ряд
новых понятий. Этот материал могут прочитать самостоятельно наиболее
подготовленные учащиеся, проявляющие повышенный интерес к математике.
На уроке, используя модели многогранников (куб,
параллелепипед, тетраэдр, призма), необходимо назвать учащимся их элементы:
вершины, грани, ребра, диагонали граней и диагонали рассматриваемых тел. Важно,
чтобы школьники усвоили эти понятия, что позволит правильно понимать
формулировки задач, не смешивая названия различных элементов в процессе их
решения. После этого вводится понятие выпуклого и не выпуклого многогранников;
обязательно учащимся показать примеры невыпуклых многогранников.
Призма А1 А2… Аn
В1 В2 …Вn определяется как многогранник,
составленный из двух равных многоугольников А1 А2… Аn
и В1 В2 …Вn,расположенных в параллельных
плоскостях, и n-параллелограммов А1 А2 В2 В1,
…, Аn А1 В1 Вn. Далее вводятся
определения элементов призмы, с помощью моделей разъясняются понятия прямой
призмы, наклонной призмы, правильной призмы. Необходимо обратить внимание
учащихся на то, что четырехугольная призма - это знакомый им параллелепипед. У
произвольного параллелепипеда все шесть граней - параллелограммы, а боковые грани
- прямоугольники, у прямоугольного параллелепипеда все шесть граней -
прямоугольники. При изучении площади поверхности призмы доказывается теорема о
площади боковой поверхности прямой призмы.
Пирамида определяется как многогранник,
составленный из n-угольника А1 А2 … Аn и
n-треугольников. При введении понятия правильной пирамиды следует акцентировать
внимание учащихся на двух моментах: основание пирамиды - правильный
многоугольник, и отрезок, соединяющий вершину пирамиды с центром ее основания,
является высотой пирамиды. Можно устно доказать, что боковые грани правильной
пирамиды - равные равнобедренные треугольники. После этого вводится понятие
апофемы правильной пирамиды (высота боковой грани правильной пирамиды,
проведенной из ее вершины), при этом нужно подчеркнуть, что этот термин
употребляется только для правильной пирамиды, хотя у неправильной пирамиды
также могут быть равны высоты боковых граней.
При изучении теоремы о площади боковой
поверхности правильной пирамиды полезна символическая запись доказательства.
Пусть сторона основания n-угольной пирамиды равна а, апофема равна d, S?
- площадь боковой грани. Тогдабок=n• S?, Sбок=n•ad,
Sбок=(n•a)•d, Sбок= Pd, где P - периметр основания
пирамиды.
Далее вводится понятие усеченной пирамиды.
Плоскость, параллельная основанию пирамиды, разбивает ее на два многогранника:
один из них является пирамидой, а другой называется усеченной пирамидой.
Усеченная пирамида - это часть полной пирамиды, заключенная между ее основанием
и секущей плоскостью, параллельной основанию данной пирамиды. При выполнении
рисунков к задачам на усеченную пирамиду удобно вначале начертить полную
пирамиду, а затем выделить усеченную пирамиду.
При введении понятия правильной усеченной
пирамиды надо отметить, что ее основания - правильные многоугольники, а боковые
грани - равные равнобедренные трапеции; высоты этих трапеций называются
апофемами усеченной пирамиды. Также выводится формула площади боковой
поверхности правильной усеченной пирамиды.
Последнее, что изучается в теме «Многогранники»
в учебнике, это симметрия в пространстве и понятие правильного многогранника.
Основными понятиями здесь являются понятия симметричных точек относительно
точки, прямой, плоскости; понятия центра, оси, плоскости симметрии фигуры. При
введении понятия правильного многогранника нужно подчеркнуть два условия,
входящие в определение: а) все грани такого многогранника - равные правильные
многоугольники; б) в каждой вершине многогранника сходится одно и то же число
ребер. В учебнике доказано, что существует пять видов правильных многогранников
и не существует правильного многогранника, гранями которого являются правильные
n-угольники при n. Целесообразно предложить учащимся изготовить дома модели
правильных многогранников. Для этой цели надо использовать развертки,
изображенные в учебнике.
Таким образом, в данном учебнике многогранники
изучаются с опорой на наглядность, предметы окружающей действительности.
Весь теоретический материал темы относится либо
к прямым призмам, либо к правильным призмам и правильным пирамидам. Все теоремы
доказываются достаточно просто, результаты могут быть записаны формулами,
поэтому в теме много задач вычислительного характера, при решении которых
отрабатываются умения учащихся пользоваться сведениями из тригонометрии,
формулами площадей, решать задачи с использованием таких понятий, как «угол
между прямой и плоскостью», «двугранный угол» и др.
Учебник Смирновой И.М. предназначен для
преподавания геометрии 10-11 классах гуманитарного профиля. По сравнению с
традиционным изложением в учебнике несколько сокращен теоретический материал,
больше внимания уделяется вопросам исторического, мировоззренческого и
прикладного характера.
Как и в, особенностью учебника является раннее
введение пространственных фигур, в том числе многогранников, «Основные
пространственные фигуры». Цель - сформировать представления учащихся об
основных понятиях стереометрии, ознакомить с пространственными фигурами и
моделированием многогранников. Вводиться понятие многогранника как
пространственной фигуры, поверхность которой состоит из конечного числа
многоугольников, называемых гранями многогранника. Стороны этих многоугольников
называются ребрами многогранника, а вершины многоугольников - вершинами
многогранника.
Учащимся демонстрируются следующие
многогранники:
куб - многогранник, поверхность которого состоит
из шести квадратов;
параллелепипед - многогранник, поверхность
которого состоит из шести параллелограммов;
прямоугольный параллелепипед - параллелепипед, у
которого грани - прямоугольники;
призма - многогранник, поверхность которого
состоит из двух равных многоугольников, называемых основаниями призмы, и
параллелограммов, называемых боковыми гранями (причем у каждого параллелограмма
два противоположных ребра лежат на основаниях призмы);
прямая призма - призма, боковые грани которой -
прямоугольники; правильная призма - прямая призма, основаниями которой являются
правильные многоугольники;
пирамида - многогранник, поверхность которого
состоит из многоугольника, называемого основанием пирамиды, и треугольников с
общей вершиной, называемых боковыми гранями пирамиды;
правильная пирамида - пирамида, в основании
которой правильный многоугольник, и все боковые ребра равны.
Показываются более сложные многогранники, в том
числе правильные, полуправильные и звездчатые многогранники. Рассматривается
несколько способов изготовления моделей многогранников из разверток и
геометрического конструктора. Моделирование многогранников служит важным
фактором развития пространственных представлений учащихся.
Таким образом, к началу непосредственного
изучения темы «Многогранники» учащиеся уже знакомы (на доступном для них
уровне) с традиционным материалом по этой теме. Появляется возможность
расширить представления учащихся о многогранниках, рассмотрев с ними более
подробно правильные, полуправильные и звездчатые многогранники.
Основная цель данного раздела - ознакомить
учащихся с понятием выпуклости и свойствами выпуклых многогранников,
рассмотреть теорему Эйлера и ее приложения к решению задач, сформировать
представления о правильных, полуправильных и звездчатых многогранниках.
Можно привести примерное тематическое
планирование данной темы.
|
Пункт
учебника
|
Содержание
|
Кол-во
часов
|
|
|
18
|
Выпуклые
многогранники
|
2
|
|
|
19
|
Теорема
Эйлера
|
2
|
|
|
20*
|
Приложения
теоремы Эйлера
|
2
|
|
|
21
|
Правильные
многогранники
|
2
|
|
|
22*
|
Топологически
правильные многогранники
|
1
|
|
|
23
|
Полуправильные
многогранники
|
2
|
|
|
23
|
Звездчатые
многогранники
|
1
|
|
Среди пространственных фигур особое значение
имеют выпуклые фигуры и, в частности, выпуклые многогранники. Данное понятие в
учебнике вводится следующим образом: многогранник называется выпуклым, если он
является выпуклой фигурой, т.е. вместе с любыми двумя своими точками целиком
содержит и соединяющий их отрезок. Далее рассматриваются свойства выпуклых
многогранников.
После изучения выпуклых многогранников
рассматривается теорема Эйлера и ее приложения. В качестве таких приложений
рассматриваются задача о трех домиках и трех колодцах, проблема четырех красок,
вводится понятие графа.
Выпуклый многогранник называется правильным,
если его гранями являются равные правильные многоугольники, и в каждой вершине
сходится одинаковое число граней. Выпуклый многогранник называется
полуправильным, если его гранями являются правильные многоугольники (возможно,
и с разным числом сторон), причем в каждой вершине сходится одинаковое число
граней. Рассматриваются пять видов правильных многогранников, некоторые виды
полуправильных и четыре звездчатых многогранника.
При изучении правильных, полуправильных и
звездчатых многогранников следует использовать модели этих многогранников,
изготовление которых описано в учебнике, а также графические компьютерные
средства.
Учебник Александрова А.Д. предназначен для
классов и школ с математической специализацией, он дает богатую математическую
информацию, развивает ученика, но является достаточно трудно усваиваемым. В
учебнике рассматриваются такие темы, которые в основной школе не доступны даже
для «сильных» учеников, например, сферическая геометрия.
Отметим особенности изучения многогранников в
данном учебнике. Во-первых, многогранники изучаются после круглых тел.
Во-вторых, при изучении многогранника и его элементов прослеживается связь с
многоугольником. Вследствие чего возможны две последовательности изложения
темы: 1) обобщить понятие многоугольника, затем разобрать аналогичные вопросы в
пространстве; 2) пользуясь, дать сначала определение многогранника, далее
обобщить понятие многоугольника. Особенностью является введение двух
определений призмы (как в учебниках, рассмотренных выше, и как цилиндр, в
основании которого лежит многоугольник), причем доказывается равносильность
этих определений. Аналогично дается другое определение пирамиде: как конус с
многоугольником в основании. Пункт содержит раздел о триангулировании
многогранника, и в нем дается другое, конструктивное определение многогранника.
«Выпуклые многогранники» впервые излагается в столь серьезном виде,
рассматривается вопрос равносильности двух определений выпуклого многогранника.
Изложение темы «Правильные многогранники» также отличается от ее изложения в
учебниках по геометрии других авторских коллективов: сначала показываются пять
типов правильных многогранников, построением доказывается, что все пять типов
правильных многогранников существуют, и только после этого доказывается, что
других правильных выпуклых многогранников быть не может. Обычно же после
определения сразу доказывалась теорема, а существование показывалось позже, что
усложняло методику рассказа.
Таким образом, учебник содержит очень богатый
теоретический материал по многогранникам, которого нет в других учебниках по
геометрии, также он может быть использован как учебник для дополнительного
изучения в основной школе. Ниже в таблице приведено примерное поурочное
планирование материала.
|
№
урока
|
Содержание
учебного материала
|
|
|
1-2
|
Обобщение
понятие многоугольника. Многогранник.
|
|
|
3-5
|
Призма,
параллелепипед. Упражнения.
|
|
|
6-10
|
Пирамида.
Виды пирамид. Упражнения.
|
|
|
11-13
|
Выпуклые
многогранники.
|
|
|
14-16
|
Теорема
Эйлера. Развертка выпуклого многогранника.
|
|
|
17-19
|
Правильные
многогранники.
|
|
Подводя итоги выше сказанного, можно сказать,
что во всех учебниках при изучении многогранников рассматривается практически
одни и те же основные темы: определение многогранника, выпуклые многогранники,
призма, пирамида, правильные многогранники. Разница лишь в глубине изучения
этих вопросов: в гуманитарных классах тема изучается более поверхностно,
практически без доказательств, в классах с углубленным изучением математики
данный вопрос рассматривается глубоко, с научными обоснованиями. Также есть
различия в некоторых дополнительных темах, например, полуправильные и
звездчатые многогранники. В настоящее время во многих общеобразовательных
школах идет обучение по учебнику, поэтому при выборе содержания можно опираться
на него.
2. Виды и роль наглядных средств при
изучении многогранников
Тема «Многогранники», как никакая другая тема
школьного курса стереометрии, за исключением, быть может, изучения круглых тел,
дает широкие возможности использования различных наглядных средств.
Наглядность является обязательным качеством
любого обучения. Путем целенаправленных действий мы формируем в сознании
учащегося некоторую систему понятий, отношений между ними. Для того чтобы
обучение было успешным, необходимо, чтобы ученик мог воспринимать эту систему и
работать с ней. Но для этого, в свою очередь, необходимо предъявить ученику
некоторую ее материальную модель. Для этого применяют наглядные средства
обучения. Например, если изучается понятие пирамиды, то такой моделью может
быть: 1) словесное описание (определение) этого понятия; 2) объемная модель
пирамиды (каркасная или сплошная); 3) ее развертка; 4) изображение пирамиды или
ее развертки на доске, на бумаге, на экране и т. п. Все перечисленные объекты
являются материальными моделями, с той или иной стороны отражающими понятие
пирамиды.
Основными наглядными средствами при изучении
многогранников являются объемные модели. Такие модели, сделанные из разных
материалов, соответствуют различным дидактическим целям.
Так, например, с помощью картонной модели можно
показать форму многогранника. Также на таких моделях удобно показать развертку
поверхности тела. Но из-за непрозрачности картона уже нельзя использовать
картонные многогранники для демонстрации сечения тел и тел, вписанных друг в
друга. Стеклянные модели рекомендуется использовать в тех случаях, когда
необходимо показать в многограннике сечение или другое вписанное в него
геометрическое тело. Деревянные модели отличаются прочностью. Проволочные
каркасные модели также находят широкое применение на уроках стереометрии. Они позволяют
показать виды, элементы и проекцию многогранника на плоскость (тень модели на
листе белой бумаги), сечение многогранника плоскостью, комбинации
геометрических тел. Такая модель является связующим звеном между объемной
моделью многогранника и чертежом на бумаге. Можно перечислить серии каркасных
моделей, которые могут быть использованы на уроке: набор моделей правильных
призм и пирамид (полных и усеченных), набор моделей четырехугольных пирамид,
вершины которых проектируются в точку пересечения диагоналей основания (кроме
основного контура, модель должна иметь высоту, диагональ основания и высоты
боковых граней), набор моделей на комбинации многогранников.
Выпускаемые промышленностью модели не всегда
могут удовлетворить потребности, возникающие при обучении школьников
математике. Поэтому учителя часто прибегают к изготовлению моделей своими
силами с привлечением учащихся. Это делается не только в тех случаях, когда в
школе отсутствуют необходимая модель, прибор или инструмент, но и когда учитель
считает, что имеющаяся модель, прибор не в полной мере способствуют ясному и
четкому восприятию изучаемого материала. Внося в модель усовершенствования,
учитель привлекает учащихся к изготовлению нового варианта модели. Это
содействует получению учащимися более глубоких и прочных знаний, умений
применять теоретический материал на практике. Модели, как фабричного, так и
самодельного изготовления могут быть использованы при введении новых понятий и
доказательстве теорем, при решении задач, при выполнении практических и
лабораторных работ.
Другим удобным видом учебного оборудования
являются резиновые штемпели (штампы) с изображением различных плоских и
объемных фигур, графиков, таблиц и т. д. К сожалению, такое средство обучения
сейчас редко встречается в школе. При использовании этого вида учебного
оборудования достаточно приложить штемпель к штемпельной подушке и прижать его
к листу бумаги, чтобы получить нужное изображение, например изображение куба
или прямоугольного параллелепипеда. При решении задач, связанных с построением
изображений куба или прямоугольного параллелепипеда, учащиеся, воспользовавшись
штемпелем, могут быстро получить в тетради правильный чертеж, что дает большую
экономию времени. Естественно, применение штемпелей недолжно привести к утрате
учащимися навыков вычерчивания фигур. Поэтому учитель должен, вначале научить
учащихся изображать фигуры на плоскости, а затем применять штемпели на уроке.
Штемпели могут использоваться учителем при подготовке многовариантных
контрольных заданий. Можно, например, заготовить 35-40 чертежей с изображением
прямоугольного параллелепипеда, чтобы затем, проставив размеры, получить набор
индивидуальных заданий.
Также при изучении многогранников можно
использовать различные рабочие и справочные таблицы. Рабочие таблицы - это
такие таблицы, по материалу которых можно организовать активную мыслительную
деятельность учащихся, как по усвоению нового теоретического материала, так и
по его закреплению. С помощью рабочих таблиц, возможно, осуществить выполнение
большого числа упражнений, способствующих выработке и закреплению у учащихся
определенных навыков, можно проводить опрос учащихся или создать проблемную
ситуацию перед всем классом. Например, при ведении понятия «пирамида» можно
использовать таблицу с изображением пирамиды, ее основных элементов и частных
видов. В отличие от рабочих таблиц справочные таблицы, т.е. таблицы для
запоминания, предназначены для длительного воздействия на зрительный аппарат
учащегося. Такие таблицы могут быть вывешены в кабинете математики на длительное
время. Таким образом, основным свойством справочных таблиц является (помимо
наглядности, которая в ряде случаев играет важную роль) их дидактическая
направленность. Таблицы эти предназначены для принудительного воздействия на
память учащегося с целью запоминания основных фактов, формул, графиков и др.
Примером таких таблиц может служить таблица «Вычисление площадей и объемов
многогранников», в которой изображены различные виды многогранников и указаны
формулы вычисления объема и площади поверхности для каждого вида.
Большие возможности воспитания самостоятельности
и активности открываются при использовании тетрадей с печатной основой. В
настоящий момент они все чаще появляются в школах. Тетради с печатной основой
предназначаются для организации самостоятельной работы на этапе закрепления и
повторения пройденного материала. Основная отличительная особенность тетради в
том, что она позволяет более рационально использовать учебное время, так как
ученики освобождаются при работе с тетрадью от механического переписывания
текста заданий и основное внимание сосредоточивают на выполнении заданий,
включенных в тетрадь. Как правило, такие тетради чаще используются в младших
классах. Тетради с печатной основой включают большое число заданий. Цель
заданий различна. Задания могут дать ученику образец способа рассуждений,
решения, данные в тетради, могут содержать пропуски в тексте, которые ученики
должны заполнить при работе с тетрадью (причем пропущены не случайные слова, а
такие, которые заставляют ученика лишний раз обратиться к определениям,
задуматься над последовательностью операций). Итак, тетрадь с печатной основой
дает возможность отрабатывать понятия и прививать учащимся навыки решения
типовых задач.
Также нельзя забывать и про такие средства
обучения как диапозитивы, кодопозитивы, компьютерные средства, которые могут
быть эффективно применены при изучении многогранников и не только их.
Нередко наглядные средства рассматривают лишь
как временную опору при начальном усвоении знаний. Сторонники такой оценки роли
наглядных средств полагают, что модели в этом случае приучают учащихся к
очевидности и поэтому не способствуют развитию логического мышления.
Выдвигается даже дидактическое правило: чем старше учащиеся, тем меньше моделей
должно применяться в преподавании математики. Принять такую точку зрения и
вытекающее из нее дидактическое правило нельзя, так как они несостоятельны.
Правильно понимаемое применение наглядных средств не только уместно, но и
необходимо на всех ступенях обучения.
Таким образом, готовясь к конкретному уроку,
учитель выбирает те средства, с которыми легче организовать необходимую работу
учащихся, т. е. наиболее в данный момент простые для их восприятия. Например,
если на уроке предполагается начать знакомство с понятием какого-то частного
вида многогранника, то наиболее удобными окажутся объемные изображения или
изображения на киноэкране. В процессе же закрепления этого понятия достаточно
просты для восприятия плоские чертежи или словесные описания.
Таким образом, чтобы некоторая материальная
модель позволяла организовать усвоение того или иного понятия, она должна не
только правильно его отражать, но и быть простой для восприятия учащихся.
3. Опорные задачи по теме
«Многогранники»
Как уже говорилось, изучение многогранников
является важнейшей частью курса стереометрии. Они дают богатый задачный
материал, как при изучении самой темы «многогранники», так и при изучении
последующих тем стереометрии. Чаще всего в учебниках мало простых задач «на
геометрические тела», поэтому на уроке удается решить всего 2-3 задачи средней
трудности. Но они не всем ученикам под силу. Если ограничиваться только такими
задачами, то многие ученики не смогут принимать активное участие в их решении,
и будут отставать. Если же специально уделять на уроке время для задач, которые
сводятся к одной-двум операциям и потому доступны для устного решения, то можно
втянуть в работу всех учеников.
Устное решение задач «на многогранники»
значительно улучшает пространственное мышление учащихся, которое играет важную
роль в стереометрии. Поэтому подробнее остановимся именно на таких задачах.
Так как основные геометрические тела, изучаемые
в школе, это призмы и пирамиды, то задачи, приведенные ниже, посвящены темам:
«Призма. Пирамида. Их сечения. Площади полной и боковой поверхностей». Кроме
того, задачи разбиты на типы: задачи на доказательство, на исследование, на
построение, на вычисление.
Большое количество задач можно предлагать для
решения вместе с готовым рисунком, когда один рисунок будет сопровождать
несколько задач, в которых идет речь об одном и том же геометрическом теле. Но
готовые рисунки сопутствуют далеко не всем задачам, поскольку само изготовление
изображения является важной частью решения. Учитель может варьировать стратегию
обучения. В одних случаях - начинать с готового рисунка, а в других
-демонстрировать рисунок (на откидной доске или на экране) только после того,
как учащиеся сами сделали нужные изображения в своих тетрадях.
4. Изучение свойств многогранников
Пространственное мышление значимо для каждого человека,
независимо от уровня его образования и вида деятельности. Значительную роль в
развитии пространственных представлений и пространственного мышления играет
изучение свойств многогранников. В то же время, в сложившейся практике изучения
геометрии, материал, связанный с многогранниками, рассматривается в конце
изучения геометрии, что связано со строгим следованием аксиоматическому методу
изложения этого курса. Изучая планиметрию, ученики не только не должны забывать
о пространственных фигурах, а наоборот, должны расширить знакомство с ними.
Ведь нас окружают реальные предметы - пространственные фигуры. Многие учащиеся,
закончив девять классов, продолжают обучение в училищах, средних специальных
заведениях, лицеях, колледжах или начинают заниматься практической
деятельностью, и им необходимы элементарные знания трехмерной геометрии.
Поэтому курс планиметрии целесообразно строить на фузионистских принципах, то
есть в органичной связи с планиметрическим материалом должны быть введены
свойства многогранников и, возможно, предусмотрено рассмотрение других
стереометрических объектов. Общеобразовательная школа должна при первой
возможности знакомить учащихся с простейшими видами многогранников, их
изображениями, изготовлением, развертками, измерениями площади поверхности и
объема, что подготовит учащихся, ориентированных на дальнейшее обучение в 10-м
классе, к лучшему восприятию систематического курса стереометрии, а учащихся,
заканчивающих обучение в 9-м классе, более полно познакомит с окружающим миром.
Распределение учебного и задачного материала,
связанного с многогранниками, по темам планиметрии

В курсе геометрии 7-9-х классов можно
рассмотреть такие многогранники, как параллелепипед, призма, пирамида, а также
правильные многогранники. Учащиеся этих классов учатся рассуждать, доказывать
различные утверждения при изучении систематического курса планиметрии, а также
хорошо представлять себе пространственные формы, видеть в них красоту.
Многогранник «определяется» в 5-6-х классах.
Определение многогранника дается на описательном уровне следующим образом.
Поверхность многогранника состоит из многоугольников. Каждый из этих
многоугольников называют гранью многогранника. Вершины этих многоугольников
являются также и вершинами многогранника, а стороны многоугольника - ребрами
многогранника. Здесь очень важно показать учащимся различные модели
многогранников. Прежде чем изучать каждый вид многогранников в отдельности,
определим общий подход к рассмотрению основных видов многогранников в 7-9-х
классах. При рассмотрении многогранников в курсе планиметрии 7-9-х классов
применим именно индуктивный путь ознакомления с основными видами
многогранников. Рассмотрение призмы целесообразно начать с частных видов призм.
А именно, рассмотреть уже знакомые виды призм, которые встречались в курсе
математики 5-6-х классов (Ходеева Т.В. Изучение свойств многогранников в курсе
математики 5-6 классов. Математика (еженедельная газета ИД «Первое сентября»),
№ 11, 13/2002), затем рассмотреть и другие. После этого можно дать общее
описание произвольной призмы. Аналогичный подход и при рассмотрении пирамиды.
При изучении основных видов многогранников в 7-9-х классах, так же как и в
5-6-х классах, нельзя дать точных определений, поэтому приводится описание многогранников
каждого вида. При рассмотрении каждого вида многогранников целесообразно
придерживаться некоторой схемы: описание данного вида многогранников;
нахождение данного вида многогранников на рисунках, чертежах, среди окружающих
предметов; изображение; развертка; некоторые свойства; сечение (имеется в виду
сечения: параллельно плоскости основания или некоторой грани, проходящие через
два не соседних ребра и другие), симметрия. Рассматривая различные виды
многогранников, с которыми уже учащиеся встречались, целесообразно напомнить
установленные свойства.
Из курса математики 5-6-х классов учащиеся уже
знакомы с кубом, прямоугольным параллелепипедом, прямой призмой. Рассмотрение
прямого и наклонного параллелепипеда, наклонной призмы возможно только после изучения
понятия параллелограмм. Итак, параллелепипед - многогранник, поверхность
которого состоит из шести параллелограммов. Здесь очень важно показать учащимся
модели различных видов параллелепипедов: прямоугольного параллелепипеда,
прямого параллелепипеда и наклонного параллелепипеда. На моделях с учащимися
полезно обсудить, какими четырехугольниками являются грани параллелепипедов
различных видов.
Свойства параллелепипеда
1. У параллелепипеда 8 вершин, 12 ребер и 6
граней.
2. Каждая грань параллелепипеда -
параллелограмм.
. Противолежащие грани параллелепипеда
равны.
. Параллельные ребра параллелепипеда
равны.
Сечение параллелограмма
1. Сечение параллелепипеда плоскостью,
параллельной грани. В сечении образуется параллелограмм.
2. Сечение параллелепипеда плоскостью,
проходящей через противолежащие ребра. В сечении образуется параллелограмм. В
некоторых случаях в сечении может образоваться ромб, прямоугольник или квадрат.
При рассмотрении каждого вида многогранников
(параллелепипеда, призмы, пирамиды) можно рассмотреть с учащимися 7-9-х классов
стандартные сечения, такие как сечение многогранника, плоскостью, параллельной
плоскости одной из граней, и сечение многогранника плоскостью, проходящей через
два не соседних параллельных ребра многогранника. При рассмотрении сечений
многогранника вид сечения учащиеся 7-9-х классов, так же как и 5-6-х классов,
определяют с помощью каркасных моделей многогранников или моделей, сделанных из
пластилина. При этом от учащихся не требуется доказывать, что в сечении образуется
та или иная фигура, главное - просто увидеть ее на моделях рассматриваемых
многогранников.
Призма - это многогранник, поверхность которого
состоит из двух равных многоугольников, называемых основаниями призмы, и
параллелограммов, называемых боковыми гранями (причем у каждого параллелограмма
две противолежащие стороны лежат на основаниях призмы).
Свойства призмы
. Основания призмы являются равными
многоугольниками.
2. Боковые грани призмы являются
параллелограммами.
. Боковые ребра призмы равны.
Сечение призмы
.Сечение призмы плоскостью, параллельной
основанию. В сечении образуется многоугольник, равный многоугольнику, лежащему
в основании.
.Сечение призмы плоскостью, проходящей через два
не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение
называется диагональным сечением призмы. В некоторых случаях может получаться
ромб, прямоугольник или квадрат.
Рассмотрение правильной призмы возможно только
после введения понятия правильный многоугольник. Однако с правильной
треугольной призмой можно познакомить учащихся гораздо раньше. А с правильной
четырехугольной призмой они знакомы еще из курса математики 5-6-х классов, так
как она представляет собой прямоугольный параллелепипед с квадратами в
основаниях. Правильная призма - прямая призма, основаниями которой являются
правильные многоугольники.
Свойства правильной призмы
. Основания правильной призмы являются
правильными многоугольниками.
2. Боковые грани правильной призмы
являются равными прямоугольниками.
. Боковые ребра правильной призмы равны.
Сечение правильной призмы
. Сечение правильной призмы плоскостью,
параллельной основанию. В сечении образуется правильный многоугольник, равный
многоугольнику, лежащему в основании.
. Сечение правильной призмы плоскостью,
проходящей через два не соседних боковых ребра. В сечении образуется
прямоугольник. В некоторых случаях может образоваться квадрат.
Из курса математики 5-6-х классов учащиеся уже
знакомы с описанием пирамиды. А именно: пирамида - многогранник, поверхность
которого состоит из многоугольника, называемого основанием пирамиды, и
треугольников с общей вершиной, называемых боковыми гранями пирамиды.
Знакомство с правильной пирамидой возможно только после изучения понятия
правильный многоугольник. Однако с правильной треугольной и правильной
четырехугольной пирамидой можно познакомить учащихся значительно раньше.
Правильная пирамида - пирамида, в основании которой лежит правильный
многоугольник и все боковые ребра равны.
Свойства правильной пирамиды
.Основание правильной пирамиды - правильный
многоугольник.
.Боковые грани правильной пирамиды -
равнобедренные треугольники.
.Боковые ребра правильной пирамиды равны.
Сечение правильной пирамиды
.Сечение правильной пирамиды плоскостью,
параллельной основанию. В сечении образуется правильный многоугольник, подобный
многоугольнику, лежащему в основании.
.Сечение правильной пирамиды плоскостью,
проходящей через два не соседних боковых ребра. В сечении образуется
равнобедренный треугольник. В некоторых случаях может образоваться равносторонний
треугольник.
С некоторыми правильными многогранниками
учащиеся уже встречались. Это треугольная пирамида и куб. Гранями треугольной
пирамиды являются правильные треугольники. Ее называют правильным тетраэдром,
что в переводе с греческого означает четырехгранник. Куб имеет шесть граней,
поэтому называется правильным гексаэдром (по-гречески «гекса» означает шесть).
Рассмотрение правильных многогранников следует начинать с тех из них, гранями
которых являются правильные треугольники. Один из таких многогранников учащимся
уже знаком - это правильный тетраэдр. Другой многогранник, гранями которого
являются правильные треугольники, изображен на рисунке 39.
Его поверхность состоит из восьми правильных
треугольников, поэтому его называют правильным октаэдром («окта» - восемь).
И третий многогранник, гранями которого являются
правильные треугольники - это правильный икосаэдр («икоса» - двадцать). Его
поверхность состоит из двадцати правильных треугольников (рис. 40).
Многогранник, гранями которого являются квадраты
- это куб. Учащимся он хорошо знаком. Многогранник, гранями которого являются
правильные пятиугольники, изображен на рисунке 41. Его поверхность состоит из
двенадцати правильных пятиугольников, поэтому его называют правильным
додекаэдром («доде» - двенадцать).
Как уже было отмечено выше, при рассмотрении
каждого вида многогранников с учащимися 7-9-х классов целесообразно
придерживаться такой же схемы, что и для 5-6-х классов, дополнительно
рассмотрев симметрию многогранников. При ее рассмотрении учащиеся 7-9-х классов
находят центр симметрии, плоскости симметрии и оси симметрии (если они
существуют) с помощью моделей многогранников. При этом полезно предложить
учащимся такое творческое и интересное задание, как изготовление моделей
рассматриваемых многогранников с указанием на них плоскостей симметрии. Такие
задания развивают пространственное мышление учащихся, дают возможность
творчески подойти к выполнению задания и, что немаловажно, повышают интерес к
предмету геометрия.
Симметрия куба
.Центр симметрии - центр куба (точка пересечения
диагоналей куба) (рис.42).
.Плоскости симметрии: три плоскости симметрии,
проходящие через середины параллельных ребер; шесть плоскостей симметрии,
проходящие через противолежащие ребра (рис.43).
.Оси симметрии: три оси симметрии, проходящие
через центры противолежащих граней; четыре оси симметрии, проходящие через
противолежащие вершины; шесть осей симметрии, проходящие через середины
противолежащих ребер (рис.44).
Симметрия прямоугольного параллелепипеда
1.Центр симметрии - точка пересечения диагоналей
прямоугольного параллелепипеда (рис.45).
.Плоскости симметрии: три плоскости симметрии,
проходящие через середины параллельных ребер (рис.46).
.Оси симметрии: три оси симметрии, проходящие
через точки пересечения диагоналей противолежащих граней (рис.47).

Симметрия параллелепипеда
Центр симметрии - точка пересечения диагоналей
параллелепипеда (рис.48).
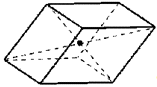
Симметрия прямой призмы
Плоскость симметрии, проходящая через середины
боковых ребер (рис.49).
Симметрия правильной призмы
1.Центр симметрии при четном числе сторон
основания - точка пересечения диагоналей правильной призмы (рис.50)
.Плоскости симметрии: плоскость, проходящая
через середины боковых ребер; при четном числе сторон основания - плоскости,
проходящие через противолежащие ребра (рис.51).
.Оси симметрии: при четном числе сторон
основания - ось симметрии, проходящая через центры оснований, и оси симметрии,
проходящие через точки пересечения диагоналей противолежащих боковых граней
(рис.52).
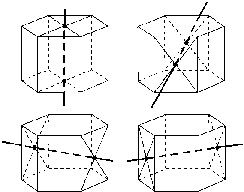
Симметрия правильной пирамиды
.Плоскости симметрии: при четном числе сторон
основания - плоскости, проходящие через противолежащие боковые ребра; и
плоскости, проходящие через медианы, проведенные к основанию противолежащих
боковых граней (рис.53).
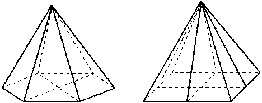
.Ось симметрии: при четном числе сторон
основания - ось симметрии, проходящая через вершину правильной пирамиды и центр
основания (рис.54).
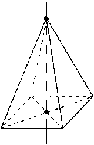
Изучение свойств многогранников
7-9 классы
Задачный материал
Задачный материал, связанный с многогранниками,
для 7-9-х классов распределен по темам планиметрии.
класс
.Основные свойства простейших геометрических
фигур. Треугольник. Параллельные прямые
.1.На верхней грани куба изображена
(заштрихована) фигура f, содержащая точки A, B, C, D и M. Является ли эта
фигура плоской? Является ли плоской фигура, составленная из двух треугольников
DD1P и DD1Q (рис.55), лежащих в передней и боковой гранях
куба?

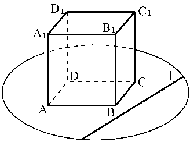
.2. На рисунке56 - плоскость нижней
грани параллелепипеда, прямая l лежит в плоскости . Постройте
точки, в которых прямая l пересекается с прямыми AB, BC, DC и AD.
.3. По рисунку57 укажите, какие прямые,
проходящие через две вершины параллелепипеда, содержатся в плоскости .
.4.Изобразите куб, обозначьте его буквами.
Обозначьте через плоскость его передней грани. Какие вершины куба
принадлежат плоскости , какие не принадлежат? Запишите знаками.
.5.Сделайте чертеж прямоугольного
параллелепипеда, обозначьте его буквами. Укажите, какие вершины принадлежат
плоскости , содержащей нижнюю грань параллелепипеда.
.6.Куб имеет длину ребра a. Каждая грань
куба представляет собой квадрат с периметром 4a. Всего у куба шесть
таких граней. Следует ли отсюда, что сумма длин ребер равна 24a?
.7.У куба шесть граней и на каждой грани четыре
прямых угла. Таким образом, на поверхности куба имеется 24 прямых угла,
образованных ребрами. Как еще можно подсчитать число прямых углов на
поверхности куба?
.8.Назовите треугольники, образующие поверхность
треугольной пирамиды (рис.58).
.9.Можно ли с помощью шести спичек составить
фигуру, состоящую из четырех одинаковых треугольников?
.10.Запишите, какие ребра куба параллельны (см.
рис.59).
.11.Сделайте чертеж параллелепипеда и обозначьте
вершины буквами. Приведите примеры пересекающихся прямых, а также примеры
непересекающихся прямых.
.12.Точки P и Q расположены внутри грани A1B1C1D1
куба. Сделайте чертеж и постройте на нем точки пересечения прямой PQ с ребрами
куба или с их продолжениями.
.13.Пересекаются ли в пространстве прямые DD1
и A1B1 (см. рис.59)? Ответьте на тот же вопрос
относительно прямых BB1 и DC.
.Смежные и вертикальные углы.
Перпендикулярные прямые. Биссектриса угла
2.1.Запишите, какие ребра куба перпендикулярны
(рис.60).
.2.Боковой гранью треугольной пирамиды SABC
является треугольник ASB с углом SAB, равным 80°. В боковой грани проведена
биссектриса AM. Чему равен угол между биссектрисой и стороной AB основания
пирамиды?
Примечание. Задача 2.1 рассматривается при изучении
перпендикулярных прямых, задача 2.2 - при изучении биссектрисы угла.
.Признаки равенства треугольников.
Равнобедренный треугольник. Равносторонний треугольник. Высота, биссектриса и
медиана треугольника

.1.Точки M и N - середины ребер куба (рис.61).
Докажите, что треугольник ADM равен треугольнику CDN. Укажите равные стороны и
равные углы в этих треугольниках.
.2.Сторона основания правильной четырехугольной
пирамиды равна 5см, а сумма периметров боковых граней 48см. Найдите длину
бокового ребра пирамиды.
.3.Найдите площадь поверхности правильной
треугольной пирамиды, длина каждого ребра которой равна a, и вычислите
ее значение при a=3,8см.
3.4.Сторона основания правильной треугольной
пирамиды больше бокового ребра на 3см, а периметр боковой грани равен 27см.
Найдите сторону основания и боковое ребро пирамиды.
.5.Боковой гранью правильной треугольной
пирамиды служит равнобедренный треугольник с углом при вершине, содержащим 52.
Найдите величину угла x между высотой боковой грани и боковым ребром пирамиды
(рис.62).
.Сумма углов треугольника. Прямоугольный
треугольник
4.1.Боковой гранью правильной треугольной
пирамиды служит равнобедренный треугольник с углом при вершине, содержащим 64.
Найдите углы при основании в этой грани.
.2.Боковой гранью правильной треугольной
пирамиды служит равнобедренный треугольник. Угол между высотой боковой грани,
проведенной к основанию, и боковым ребром пирамиды равен 34°. Найдите углы
боковой грани.
.3.Боковой гранью правильной четырехугольной
пирамиды служит равнобедренный треугольник с углом при основании, содержащим
35°. Найдите величину угла между медианой боковой грани, проведенной к
основанию, и боковым ребром пирамиды.

4.4.Дана треугольная пирамида SABC (рис.63).
Боковая грань SAB является прямоугольным треугольником с прямым углом SAB. Угол
ASB в два раза меньше угла ABS. Найдите острые углы грани SAB.
.5. На рисунке 64 изображен куб, в верхней грани
которого проведена диагональ A1C1. Является ли
треугольник A1C1B1, расположенный в верхней
грани, равнобедренным? Является ли он на чертеже равнобедренным? Какие стороны
этого треугольника, расположенного на поверхности куба, равны? Какие углы
равны?
.6.Дан куб (рис.65). На поверхности куба
изображен (заштрихован) треугольник BCC1. Назовите в этом
треугольнике гипотенузу и катеты и найдите углы C1BC и BC1C.
.Геометрические построения
5.1.Дана четырехугольная пирамида SABCD (рис.
66). Разделите AB и BC на две равные части.
.2.Разделите ребро SA четырехугольной пирамиды
SABCD на четыре равные части.
.3.В грани ASB треугольной пирамиды SABC
постройте медианы.
.4.Точка K - середина бокового ребра SC
треугольной пирамиды SABC (рис.67). Треугольник AKB является сечением пирамиды.
Постройте медианы треугольника AKB.
.5.В правильной треугольной пирамиде SABC
постройте медиану AM треугольника ABC к стороне BC и медиану SM треугольника
BSC к стороне BC. Сколько перпендикулярных прямых проходит через точку M к
стороне BC?
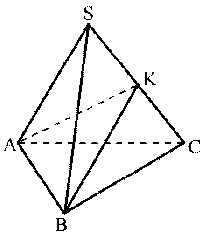
6.Четырехугольники. Теорема Фалеса.
Средняя линия треугольника

6.1.Нарисуйте развертку прямой призмы, в
основании которой лежит параллелограмм.
.2.Нарисуйте развертку прямой призмы, в
основании которой лежит: а) ромб; б) прямоугольник; в) квадрат.
.3.Нарисуйте развертку куба. Если это возможно,
то нарисуйте различные варианты развертки куба.
.4.Через середины боковых ребер правильной
четырехугольной пирамиды проведено сечение, параллельное основанию. Найдите
длины сторон сечения, если в основании пирамиды лежит квадрат, длина стороны
которого 6см (рис.68).
.5.Через середины боковых ребер правильной
треугольной пирамиды проведено сечение, параллельное основанию. Найдите
периметр сечения, если длина стороны основания равна 10 см.
.6.Нарисуйте развертку прямой призмы, в
основании которой лежит трапеция.
.7.Нарисуйте развертку наклонной призмы, в
основании которой лежит: а) параллелограмм; б) ромб; в) прямоугольник; г)
квадрат; д) трапеция.
7. Теорема Пифагора. Косинус угла.
Перпендикуляр и наклонная. Соотношения между углами и сторонами в прямоугольном
треугольнике. Значения синуса, косинуса и тангенса некоторых углов
.1.Вычислите периметр диагонального сечения
куба, ребро которого равно 5см (рис.69).
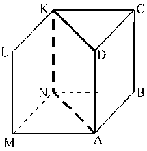
.2.Вычислите площадь диагонального сечения куба,
ребро которого равно 6см.
.3.Вычислите диагональ куба, ребро которого
равно 4см (рис.70).
.4.Сторона основания правильной треугольной
пирамиды равна 10см, а боковое ребро 13см. Найдите биссектрису боковой грани,
проведенную из вершины пирамиды.
.5.Вычислите длины граней прямоугольного
параллелепипеда (бруска) с размерами 3x5x8(см).
.6.На рисунке 71 изображен куб, в верхней грани
которого проведены отрезки B1M и B1N. Какой из отрезков B1N,
B1M или B1A1 имеет наименьшую и какой имеет
наибольшую длину: а) на кубе; б) на чертеже.
7.7.Может ли высота пирамиды быть больше длины
бокового ребра SB (рис.72)?
.8.Длина стороны основания правильной
четырехугольной пирамиды 12см, а высота пирамиды 26см. Вычислите длину бокового
ребра пирамиды.
.9.В основании прямой призмы лежит равнобокая
трапеция с основаниями 5м и 17м (рис.73). Диагональ боковой грани AA1D1D
равна 10см. Найдите расстояние между ребрами D1C1 и AB
призмы.
7.10.Длина стороны основания правильной
четырехугольной пирамиды равна 6см, а высота пирамиды 13см (рис.74). Вычислите
величину угла наклона бокового ребра пирамиды к диагонали основания.
.11.В основании треугольной пирамиды SABC лежит
равносторонний треугольник со стороной 9см. Боковой гранью SAB является
прямоугольный треугольник с прямым углом A. Ребро SA равно 40см. Найдите
неизвестную сторону, и острые углы этой грани.
.12.Основанием четырехугольной пирамиды SABCD служит
квадрат со стороной 8см. Боковая грань SBC является прямоугольным треугольником
с прямым углом BSC. Угол наклона ребра SB к ребру BC основания равен 70°30'.
Найдите неизвестные стороны и острый угол SBC.
8.Декартовы координаты на плоскости
9.Движение
.1.Приведите примеры изображений предметов
реального мира, являющихся симметричными фигурами. Укажите для каждого примера
ось симметрии или центр симметрии.
.2.Приведите примеры многогранников, являющихся
симметричными фигурами. Изобразите их. Укажите для каждого примера ось
симметрии или центр симметрии.
10.Векторы
.1.На рисунке 75 изображен куб и показан
вектор,изображаемый направленным отрезком, идущим от одной вершины куба к
противоположной вершине. Сколькими способами можно представить вектор в виде суммы
трех векторов, идущих по ребрам куба?
10.2.Вычислите длину диагонали AC1
параллелепипеда ABCDA1B1C1D1, если
его ребра имеют длины 5см, 4см, 5см.
.3.Докажите, что в треугольной пирамиде (рис.
76) длина отрезка, соединяющего середины двух противоположных ребер, меньше
полусуммы длин двух других противоположных ребер.
.4.Докажите, что в прямоугольном параллелепипеде
(рис.77) боковое ребро AA1 перпендикулярно каждой диагонали основания.
.5.В прямоугольном параллелепипеде (рис. 77) с
длинами ребер AB=3см, AD=5 см, AA1=7см вычислите угол между
диагональю AC1 и диагональю AC нижнего основания.
10.6.В пирамиде ABCD точки M и N - середины
ребер AB и CD. Докажите, что если AC = AD = BC = BD, то прямые AB, CD и MN
попарно перпендикулярны.
.7. Ребра AB и CD пирамиды ABCD перпендикулярны.
Докажите, что AC2 -AD2 = BC2 -BD2.
10.8.Диагонали трех граней прямоугольного
параллелепипеда, сходящиеся в одной вершине, имеют длины a, b и c.
Найдите длины ребер параллелепипеда.
.9.В треугольной пирамиде SABC SD - медиана
боковой грани SBC (рис. 78). Выразите через векторы  ,
и указанные на рисунке, следующие векторы:
,
и указанные на рисунке, следующие векторы: 
.10.В прямоугольном параллелепипеде (рис.39)
точки M, K, T - середины ребер. Выразите через векторы  следующие
векторы:
следующие
векторы: 
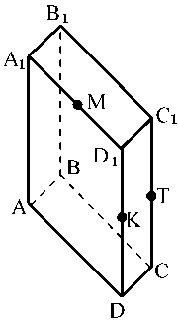
.11.В треугольной призме (рис. 80) точки M, N и
P - середины ребер A1A, C1C и B1C1
соответственно. Выразите через  следующие векторы:
следующие векторы: 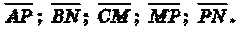
класс
11.Подобие фигур
.1.На рисунке 81 изображен прямоугольный
параллелепипед с квадратным основанием и подобный ему параллелепипед. Длины
каких отрезков можно узнать, если известно, что AB=MN1=5 см, NP = 3
см?
.2.Через середины боковых ребер правильной
пирамиды проведено сечение (рис.82). Найдите длины сторон сечения, если в
основании пирамиды лежит квадрат, длины сторон которого 6 см.
.3.В правильной треугольной пирамиде со стороной
основания 18см и боковым ребром 27см проведено сечение (рис. 83) так, что оно
отсекает от каждого бокового ребра пирамиды отрезок 9см, считая от вершины
пирамиды. Найдите длину основания сечения.

.4.Правильная четырехугольная пирамида со
стороной основания 8,5см и боковым ребром 13,6см (рис.84) пересечена
плоскостью. Найдите длину стороны получившегося сечения, если каждый из
отрезков AA1, BB1, CC1 и DD1 имеет
длину 8,8см.

.Решение треугольников
.1.Основанием параллелепипеда служит
параллелограмм со сторонами a и b и острым углом .
Найдите диагонали основания.
.2.Основанием наклонного параллелепипеда ABCDA1B1C1D1
служит ромб. Сторона ромба равна 5см, боковое ребро равно 6см, а синус угла A1AB
равен 0,6. Найдите диагонали боковой грани A1ABB1.
13.Многоугольники. Выпуклые
многоугольники.
Правильные многоугольники
.1.Углы выпуклого четырехугольника, лежащего в
основании призмы, пропорциональны числам 2, 3, 3, 4. Найдите углы основания
призмы.
.2.Сколько сторон имеет основание правильной
пирамиды, если каждый из внутренних углов основания равен 150 ?
.3.Основанием правильной пирамиды служит
многоугольник, у которого каждый из внешних углов основания равен 36. Какая это
пирамида?
.4.Из заготовки цилиндрической формы следует
выточить правильную треугольную призму (рис. 85) с возможно большей стороной
основания. Найдите длину стороны основания призмы, если диаметр заготовки равен
50 мм.
14.Площади фигур
.1.Чему равна площадь поверхности прямоугольного
параллелепипеда, у которого длины ребер, исходящих из одной вершины, равны a,
b, c?
14.2.Вычислите площадь диагонального сечения
куба (рис. 86), ребро которого равно 4 см.
.3.Сколько краски потребуется, чтобы окрасить
куб с ребром 2,5 см, если на покраску одного квадратного метра требуется 200 г
краски?
.4.Вычислите площадь полной поверхности
правильной четырехугольной призмы, сторона основания которой равна 3 см, а
высота 7см.
.5.На рисунке 87 изображена развертка
четырехугольной призмы. Выполните необходимые измерения и вычислите площадь
полной поверхности призмы.
.6.Вычислите площадь боковой поверхности
правильной четырехугольной пирамиды, сторона основания которой равна 12 см, а
боковое ребро 20 см (основанием правильной пирамиды является квадрат, а все
боковые ребра имеют одинаковую длину).
.7.Найдите площадь полной поверхности правильной
треугольной пирамиды, длина каждого ребра которой равна a, и вычислите
ее значение при a = 3,8 см.
.8.Вычислите площадь боковой поверхности
правильной шестиугольной призмы, сторона основания которой равна 8,3 см, а
боковое ребро 12 см.
.9.Найдите площадь боковой поверхности
правильной шестиугольной пирамиды, длина стороны основания которой равна a,
а боковое ребро 2a, и вычислите ее значение при a=7,5 см.
Вычислите также площадь полной поверхности этой пирамиды.
Заключение
В чем сущность современной математики? Л.Д.
Кудрявцев так отвечает на этот вопрос: «Математическая модель - это логическая
структура, у которой описан ряд отношений между ее элементами. Математика представляет
собой стройную и глубокую совокупность знаний о математических моделях со
своими проблемами, с собственными путями развития, обусловленными внутренними и
внешними причинами и задачами». Как бы продолжая мысль Л.Д. Кудрявцева,
академик В.И. Арнольд пишет: «Умение составлять адекватные математические
модели реальных ситуаций должно составлять неотъемлемую часть математического
образования».
Геометрическое моделирование - это
математическое моделирование геометрическими методами. Так же, как с аксиоматическим
методом школьники знакомятся на примере построения курса геометрии, и к
математическому моделированию можно приобщать учащихся на примере моделирования
геометрических фигур. Рисунки в действующих школьных учебниках отличаются от
тех, которые можно было бы называть моделями, так же, как схема метро
отличается от тех, которые можно было бы называть моделями, так же, как схема
метро отличается от топографической карты местности. Что знали бы школьники о
географии, если бы они изучали ее только по схемам? Изучение географии
немыслимо без контурных карт. Геометрия же в школе, как привило, изучается без
использования печатных материалов с изображениями геометрических тел. Опыт
показывает, что при использовании готовых рисунков к решаемым задачам число учащихся,
способных решить эти задачи самостоятельно, увеличивается в 4-5 раз. Если
учащиеся усвоили азы геометрического моделирования и в состоянии применять его
для исследования свойств геометрических тел, то значение этого факта для их
математического образования и развития функций головного мозга переоценить
невозможно
Целью данной работы было рассмотрение
особенностей использования моделей при решении стереометрических задач (на
примере изучения темы «Многогранники»). В связи, с чем были выполнены следующие
задачи: были рассмотрены различные подходы к определениям многогранника,
выпуклого многогранника и правильного многогранника, а также были сделаны
выводы о том, какие подходы целесообразнее использовать в школе. Кроме того,
были рассмотрены особенности изучения темы в учебниках разной направленности:
общеобразовательной, гуманитарной, с математическим уклоном. Были рассмотрены
также различные средства обучения, которые могут быть использованы при изучении
данной темы. И, наконец, были подобраны опорные задачи, которые можно
использовать на уроке при изучении данной темы и разработана серия уроков с
использованием моделей при решении стереометрических задач.
Таким образом, в данной работе были рассмотрены
основные, общие особенности использования моделей при решении стереометрических
задач (на примере изучения темы «Многогранники»).
Список использованной литературы
1. Автономова Т.В. Основные
понятия и методы школьного курса геометрии: Книга для учителя./ Т.В.
Автономова, Б.И. Аргунов. - М.: Просвещение, 1988.
2. Александров А.Д. Геометрия
для 10-11 классов: Учеб. Пособие для учащихся шк. и классов с углубл. изуч.
математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. - М.: Просвещение,
1992. - 464 с.
. Александров А.Д. Что такое
многогранник? / А.Д. Александров// Математика в школе. - 1981. - № 1-2.
. Атанасян Л.С. Геометрия:
Учеб. для 10-11 кл. общеобразоват. учреждений. / Л.С. Атанасян, В.Ф. Бутузов,
С.Б. Кодомцев и др. - М.: Просвещение, 1998. - 207 с.
. Бескин Л.Н. Стереометрия. /
Л.Н. Бескин. - М.: Просвещение, 1971.
. Болтянский В.Г. Выпуклые
многоугольники и многогранники. / В.Г. Болтянский, И.М. Яглом // Математика в
школе. - 1966. - № 3.
. Болтянский В.Г.
Элементарная геометрия: Кн. для учителя. / В.Г. Болтянский. - М.: Просвещение,
1985. - 320 с.
. Веселовский С.Б.
Дидактические материалы по геометрии для 11 класса. / С.Б. Веселовский, В.Д.
Рябчинская. - М.: Просвещение, 1998. - 96 с.
. Глаголев Н.А. Геометрия:
Стереометрия. / Н.А. Глаголев, А.А. Глаголев. - М.: Учпедгиз, 1958.
. Глейзер Г.И. История
математики в школе IX-X классы - М.; Просвещение, 1983
. Джордж Пойа. Математическое
открытие. / Джордж Пойа. - М.: Наука, 1976.
. Замечательные ученые. Под
ред. Капицы С. П. - М.; издательство «Наука», 1980
. Земляков А.Н. Геометрия в 10
классе: Метод. рекомендации к преподаванию курса геометрии по учеб. пособию
А.В. Погорелова: Пособие для учителя. / А.Н. Земляков. - М.: Просвещение, 1986.
- 208 с.
. Зив Б.Г. Задачи к урокам
геометрии. 7-11 классы. / Б.Г. Зив. - С.-Петербург, 1998.
. Зив Б.Г. Задачи по
геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив,
В.М. Мейлер, А.Г. Баханский. - М.: Просвещение, 2000.
. Каченовский М.И.
Математический практикум по моделированию. / М.И. Каченовский. - М.:
Просвещение, 1959.
. Киселев А.П. Геометрия:
Учебник для 9-10 классов средней школы. / А.П. Киселев. - М.: Учпедгиз, 1956.
. Клопский В.М. Геометрия:
Учебное пособие для 9 и 10 классов средней школы. / В.М. Клопский, З.А. Скопец,
М.И. Ягодовский / Под. ред. З.А. Скопеца. - М.: Просвещение, 1979.
. Люстерник Л.А. Выпуклые
фигуры и многогранники. / Л.А. Люстерник. - М.: Государственное издательство
технико-теоретической литературы, 1956.
. Методика преподавания
геометрии в старших классах средней школы. / Под. ред. А.И. Фетисова. - М.:
Просвещение, 1967.
. Методика преподавания
математики: Общая методика. / Составители: Р.С. Черкасов, А.А. Столяр. - М.:
Просвещение, 1985.
. Паповский В.М. Углубленное
изучение геометрии в 10-11 классах: Метод. рекомендации к преподаванию курса
геометрии в 10-11 кл. по учеб. пособию А.Д. Александрова, А.Л. Вернера, В.И.
Рыжика: Кн. для учителя. / В.М. Паповский. - М.: Просвещение, 1993. - 223 с.
. Петрова Е.С. Теория и
методика обучения математике: Учеб.-метод. пособие для студ. мат. спец.: В 3 ч.
Ч. 1. Общая методика. / Е.С. Петрова - Саратов: Изд-во Сарат. ун-та, 2004. - 84
с.
. Погорелов А.В. Геометрия:
Учеб. для 7-11 кл. сред. шк. / А.В. Погорелов. - М.: Просвещение, 1990. - 384
с.
. Преподавание геометрии в
9-10 классах. / (сб. статей) сост. З.А. Скопец, Р.А. Хабиб. - М.: Просвещение,
1980.
. Саакян С.М. Изучение темы
«Многогранники» в курсе 10 класса. / С.М. Саакян, В.Ф. Бутузов. // Математика в
школе. - 2000. - № 2.
. Сверчевская И.А. Устные
задачи по теме «Пирамида». / И.А. Сверчевская. // Математика в школе. - 2003. -
№ 7.
. Сверчевская И.А. Устные
задачи по теме «Призма». / И.А. Сверчевская. // Математика в школе. - 2003. - №
6.
. Смирнова И.М. В мире
многогранников: Кн. для учащихся. / И.М. Смирнова. - М.: Просвещение, 1995. -
144 с.
. Смирнова И.М. Геометрия:
Учеб. пособие для 10-11 кл. гуманит. Профиля. / И.М. Смирнова. - М.:
Просвещение, 1997. - 159 с.
. Смирнова И.М. Об
определении понятия правильного многогранника. / И.М. Смирнова. // Математика в
школе. - 1995. - № 3.
. Смирнова И.М. Уроки
стереометрии в гуманитарных классах. Изучение многогранников. / И.М. Смирнова.
// Математика в школе. - 1994. - № 4.
. Ходеева Т. Свойства
многогранников. / Т. Ходеева. // Математика. - 2002. - № 11.
. Юшкевич Ф.П. История
математики в России. - М.; издательство «Наука», 1968.
Приложение 1
Урок повторения по теме «Многогранники» (10
класс).
Урок был проведен в 10 классе после изучения
основных многогранников перед изучением правильных многогранников и симметрии.
Цели:
) повторить основные виды многогранников (призмы
и пирамиды), их частные виды;
) повторить основные формулы для нахождения
площади поверхности многогранников и его частных видов;
) решить задачи разного уровня сложности по
данной теме с применением уже известных знаний по многогранникам.
Оборудование: справочная таблица «Вычисление
площадей и объемов многогранников», которая содержит 4 столбца: вид
многогранника, чертеж, площадь боковой и полной поверхности, объем; готовые
чертежи на отвороте доски для решения задач.
Ход урока:
) Организационный момент.
) Актуализация знаний.
Проводится фронтальная работа по таблице.
Листочками на таблице закрыты названия многогранников, основные формулы и
чертежи. Постепенно открываются чертежи, учащиеся по чертежу называют вид
многогранника и основные формулы нахождения его полной и боковой поверхности.
Колонка таблицы с формулами объема в работе не участвует, так как объем
изучается в 11 классе. Таким образом, учащиеся вспоминают все необходимые факты
для решения задач.
)Решение задач.
На уроке предлагается решить две задачи по
готовым чертежам (устное решение), две задачи письменно с построением чертежа и
дополнительную задачу более сильным ученикам.
Задача 1. Дано: ABCDA1B1C1D1
- куб. Найдите: tg б.
Задача 2.Дано: DABC - правильная треугольная
пирамида, DO (ABC), AB = 3·DO. Найдите: б.
Задачи 1 и 2 имеют своей целью повторение
некоторых фактов планиметрии и ранее изученных тем по стереометрии (например,
перпендикулярность прямой и плоскости) и использование их в решении задач. При
решении задачи, как правило, затруднения не возникают, но можно решение задачи
2 записать в тетрадь (что и было, сделано на уроке).
Задача 3. В основании пирамиды DABC лежит
прямоугольный треугольник ABC, C = 90°, A = 30°, BC = 10. Боковые ребра
пирамиды равнонаклонены к плоскости основания. Высота пирамиды равна 5. Найдите
ребра пирамиды и площадь боковой поверхности пирамиды.
Вычисление длины ребер в задаче 3 происходит без
затруднений, площадь вычисляется немного сложнее. Но главная особенность данной
задачи в том, что необходимо понять, куда падает высота и чем является ее
основание. (При проведении урока как раз этот момент и вызвал затруднение.)
Задача 4. В прямом параллелепипеде ABCDA1B1C1D1
основанием служит ромб. Сторона ромба равна a, BAD = 60°. Диагональ
параллелепипеда B1D составляет с плоскостью боковой грани угол 45°.
Найдите площадь полной поверхности параллелепипеда.
Задача 4 сложна тем, что, во-первых, в ней не
все данные представлены числами, во-вторых, сложности возникают при определении
угла между B1D и плоскостью боковой грани (задача была полностью
разобрана на доске).
Задача 5. (дополнительная) В правильной
четырехугольной пирамиде сторона основания равна a. Угол между смежными
боковыми гранями равен 2б. Найдите площадь боковой поверхности пирамиды.
) Подведение итогов. По мере решения задачи
проверяются, в конце урока даются указания для решения пятой задачи.
Вывод: урок поставленной цели достиг, учащиеся
повторили основные виды многогранников, решили задачи разного уровня сложности,
кроме того, повторили такие факты по планиметрии, как вычисление площадей
многоугольников, и по стереометрии: угол между плоскостями, между прямой и
плоскостью и другие. В целом уровень сложности задач соответствовал уровню
подготовки учеников, и больших проблем при решении задач не возникло.
Приложение 2
Различные доказательства теоремы Эйлера.
Современная теория многогранников берет свое
начало с работ Леонарда Эйлера (1707-1783) - одного из величайших математиков
мира, работы которого оказали решающее влияние на развитие многих разделов
математики. Л. Эйлер был не только выдающимся математиком, но и крупной
творческой личностью. Им было написано около 760 научных статей для журналов,
40 книг, 15 работ для различных конкурсов. Поражает работоспособность ученого,
росшая на протяжении всей жизни. Так, в первые 14 лет научной деятельности им
было написано 80 работ объемом около 4000 печатных листов, а в последние 14 лет
жизни, несмотря на тяжелую болезнь - слепоту, опубликовано свыше 359 работ
общим объемом приблизительно 8000 печатных листов. Многие рукописи Эйлера
сохранились до наших дней. Эйлер долгое время (с 1727 по 1741 год и с 1766 до
конца жизни) жил и работал в России, был действительным членом Петербургской
академии наук, оказал большое влияние на развитие русской математической школы,
на подготовку кадров ученых - математиков и педагогов России.
Работы Эйлера дали толчок к постановке и решению
различных проблем, способствовали развитию многих разделов математики.
Математики последующих поколений учились у Эйлера. Например, французский ученый
П. С. Лаплас говорил: «Читайте Эйлера, он учитель всех нас».
В 1752 году Эйлером была доказана ставшая
знаменитой теорема о числе граней, вершин и ребер выпуклого многогранника. Она
была помещена в работе «Доказательство некоторых замечательных свойств, которым
подчинены тела, ограниченные плоскими гранями».
Рассмотрим различные доказательства этой
теоремы. В дальнейшем данный материал можно использовать как для факультативных
и кружковых занятий, так и для самостоятельного изучения учениками.
Прежде чем рассматривать доказательство,
обратимся к следующей таблице (Г- число граней многогранника, В - вершин, Р -
ребер ):
|
Название
многогранника
|
Г
|
В
|
Р
|
|
|
Тетраэдр
|
4
|
4
|
6
|
|
|
Четырехугольная
призма
|
6
|
8
|
12
|
|
|
Семиугольная
пирамида
|
8
|
8
|
14
|
|
|
Пятиугольная
бипирамида
|
10
|
7
|
15
|
|
|
Правильный
додекаэдр
|
12
|
20
|
30
|
|
Теперь найдем сумму Г+В-Р для каждого из
представленных в таблице многогранников. Во всех случаях получилось: Г+В-Р=2.
Справедливо это только для выбранных многогранников? Оказывается это
соотношение справедливо для произвольного выпуклого многогранника. Это свойство
впервые было подмечено и затем доказано Л. Эйлером.
Теорема Эйлера. Для любого выпуклого многогранника
справедливо соотношение Г+В-Р=2 (*), где Г - число граней, В - число вершин и Р
- число ребер данного многогранника.
Доказательство. Существует множество различных
доказательств теоремы Эйлера. Предлагается рассмотреть три наиболее интересных
из них.
) Наиболее распространенный способ, берущий свое
начало в работе самого Эйлера и развитый в работе французского математика
Огюста Коши (1789 - 1857) «Исследование о многогранниках» (1811 г.),
заключается в следующем. Представим поверхность данного многогранника сделанной
из эластичного материала. Удалим (вырежем) одну из его граней и оставшуюся
поверхность «растянем» на плоскость. Тогда на плоскости получается сетка,
содержащая S=Г-1 областей
(которые по-прежнему назовем гранями), В вершин и Р ребер (которые могут
искривляться). Для данной сетки нужно доказать соотношение
S+В-Р=1,
тогда для многогранника будет справедливо
соотношение.
Докажем, что соотношение не меняется, если в
сетке провести какую-либо диагональ. Действительно, после проведения некоторой
диагонали в сетке будет S+1
граней, В вершин и Р+1 ребро, т.е.
(S+1)+В-(Р+1)=Г?+В-Р.
Пользуясь этим свойством, проведем в сетке
диагонали, разбивающие ее на треугольники (диагонали изображены пунктирами), и
докажем соотношение методом математической индукции по числу n треугольников в
сетке.
Пусть n=1, т.е. сетка состоит из одного
треугольника. Тогда S=1, В=3, Р=3
и выполняется соотношение. Пусть теперь соотношение имеет место для сетки,
состоящей из n треугольников. Присоединим к ней еще один треугольник. Его можно
присоединить следующими способами:
. как ABC. Тогда сетка состоит из S+1
граней, В+1 вершин и Р+2 ребер, и, следовательно,
(S+1)+(В+1)-(Р+2)=Г?+В-Р;
. Как MNL. Тогда сетка состоит из S+1
граней, В вершин и Р+1 ребер, и, следовательно,
(S+1)+В-(Р+1)=S+В-Р.
Таким образом, в обоих случаях, т.е. при любом
присоединении (n+1)-го треугольника, выражение не меняется, и если оно
равнялось 1 для сетки из n треугольников, то оно равняется 1 и для сетки из
(n+1) треугольника. Итак, соотношение имеет место для любой сетки из
треугольников, значит, для любой сетки вообще. Следовательно, для данного
многогранника справедливо соотношение. Такое доказательство предложено в.
)Способ доказательства теоремы Эйлера, связанный
с нахождением суммы плоских углов выпуклого многогранника. Обозначим ее Sа.
Напомним, что плоским углом многогранника являются внутренние плоские углы его
граней.
Например, найдем Sа
для
таких многогранников:
а) тетраэдр имеет 4 грани - все треугольники.
Таким образом, Sа
=
4р;
б) куб имеет 6 граней - все квадраты. Таким
образом, Sа =
6?р = 12р;
в) возьмем теперь произвольную пятиугольную
призму. У нее две грани - пятиугольники и пять граней - параллелограммы. Сумма
углов выпуклого пятиугольника равна 3р. (Напомним, что сумма внутренних углов
выпуклого n-угольника равна р (n-2).) Сумма углов параллелограмма равна 2р.
Таким образом,
1=16р.
Итак, для нахождения Sа
мы вычисляли сначала сумму углов, принадлежащих каждой грани. Воспользуемся
этим приемом и в общем случае.
Введем следующие обозначения: S1, S2,
S3, …, Sr - число сторон 1, 2, 3-й и т.д. последней грани
многогранника. Тогда
а
= р
(S1-2)+ р
(S2-2)+…+ р
(Sr-2) = р
(S1 +S2 +S3 +…+Sr - 2Г
).
Далее найдем общее число сторон всех граней
многогранника. Оно равно S1
+S2
+S3
+…+Sr. Так как каждое
ребро многогранника принадлежит двум граням, имеем:
S1 +S2 +S3 +…+Sr
= 2•Р
(Напомним, что через Р мы обозначили число ребер
данного многогранника.) Таким образом получаем:
Sа
= 2р (Р-Г). (1)
Сосчитаем теперь Sа
другим способом. Для этого будем менять форму многогранника таким образом,
чтобы у него не менялось число Г, В и Р. При этом может измениться каждый
плоский угол в отдельности, но число Sа
останется прежним. Выберем такое преобразование многогранника: примем одну из
его граней за основание, расположим его горизонтально и «растянем» для того,
чтобы на него можно было спроектировать Другие грани многогранника. Например,
на рисунке 4.а показано, к чему мы придем в случае тетраэдра, а на рисунке 4.б
- в случае куба. На рисунке 5 показан многогранник произвольного типа.
Заметим, что спроектированный многогранник
представляет слившиеся две наложенные друг на друга многоугольные пластины с
общим контуром, из которых верхняя разбита на (Г-1) многоугольник, а нижняя на
грани не делится. Обозначим число сторон внешнего окаймляющего многоугольника
через r. Теперь найдем Sа
спроектированного многогранника Sа
состоит из следующих трех сумм:
) Сумма углов нижней грани, у которой r сторон,
равна р (r-2).
) Сумма углов верхней пластины, вершинами
которых являются вершины нижней грани, тоже равна р (r-2).
) Сумма «внутренних» углов верхней пластины
равна 2р (В-r), так как верхняя пластина имеет (В-r) внутренних вершин и все
углы группируются около них. Итак,
Sа
= р (r-2) + р (r-2) + 2р (В-r) = 2рВ - 4р. (2)
Таким образом, сравнивая выражения (1) и (2),
получаем:
Г + В - Р = 2,
что и требовалось доказать.
Этот способ доказательства теоремы Эйлера
рассмотрен в книге американского математика и педагога Джорджа Пойа.
)Способ, предложенный математиком Л.Н. Бескиным.
Здесь, как и в случае 1), вырезаем одну грань
многогранника и оставшуюся поверхность растягиваем на плоскость. При этом на
плоскости получается некоторая плоская фигура.
Представим себе, что эта плоская фигура
изображает собой остров, который со всех сторон окружен морем и состоит из
отдельных полей - граней, отделенных друг от друга и от воды плотинами -
ребрами.
Начнем постепенно снимать плотины, чтобы вода
попала на поля. Причем плотину можно снять, только в том случае, если она
граничит с водой, лишь с одной стороны. Снимая очередную плотину, мы орошаем
ровно одно поле. Покажем теперь, что число всех плотин (т.е. Р - число ребер
взятого многогранника) равно сумме чисел снятых и оставшихся плотин.
Итак, число снятых плотин равно (Г-1). Действительно,
снимая плотины, которые омывает вода только с одной стороны, мы оросили все
поля (т.е. грани, число которых равно (Г-1), так как одна грань была сначала
вырезана). На рисунке 6 номера 1, 2, 3, …,15 показывают порядок снятия плотин.
Число оставшихся плотин равно (В-1). Покажем это, наша система изображена после
снятия всех возможных плотин. Больше ни одну плотину снять нельзя, так как они
омываются с двух сторон. Далее никакие две вершины системы, например B и D, не
могут соединяться двумя путями, так как в противном случае получился бы
замкнутый контур, внутри которого не было бы воды, что противоречит тому, что
все поля орошены водой. Отсюда следует, что в оставшейся системе плотин должен
быть тупик, т.е. вершина, в которую ведет одно единственное ребро. Выберем
какую-либо вершину, например вершину А, и пойдем по пути, составленному из
плотин, причем не будем проходить никакую вершину дважды. В конце концов, так
как число вершин, конечно, мы придем в тупик (например, в вершину G). Тогда
отрезок-тупик, т.е. вершину G и прилежащее к ней ребро-плотину, отрежем. В
оставшейся системе опять выберем какую-нибудь вершину, пойдем от нее и отрежем
получившийся тупик. Поступая так, мы, наконец, придем к системе, в которой нет
плотин, а имеется только одна вершина, которая останется после отрезания
последнего тупика. Таким образом, число оставшихся плотин равно (В-1).
Окончательно получаем:
Р = ( Г - 1 ) + ( В - 1 ),
откуда
Г + В - Р = 2.
Теорема доказана.