Разработка теоретически обоснованной методики обучения, исследования и построения графиков элементарных функций

Введение

Материал, связанный с функциями, составляет значительную часть школьного курса математики. Это объясняется тем, что функции широко используются в различных разделах математики, в решении разных прикладных задач. Развитие функциональных представлений в курсе изучения алгебры и начал анализа на старшей ступени обучения помогает старшеклассникам получить наглядные представления о непрерывности и разрывах функций. Узнать о непрерывности любой элементарной функции на области ее применения, научиться строить их графики и обобщить сведения об основных элементарных функциях.

Функция - это одно из основных понятий математики. Изучение функций в школьном курсе математике основано на знании элементарных функций.

Объектом исследования является процесс обучения алгебре и началам анализа в средней общеобразовательной школе.

Предмет исследования - содержание и методические особенности обучения школьников базисным элементарным функциям.

Цель - состоит в разработке теоретически обоснованной методики обучения исследования и построения графиков элементарных функций.

Для реализации поставленной цели решались следующие задачи:

1. Овладение методикой исследования, обобщение и логическое изложение материала;

2. Систематизация и углубление теоретических и практических знаний по теме "Исследование и построение графиков функции".

3. Отбор содержания и разработка рабочей тетради для учащихся средних общеобразовательных учреждений.

Структура выпускной квалификационной дипломной работы следующая:

Первая глава содержит теоретический материал по общим сведениям об элементарных функциях .

Здесь рассматриваются такие функции, как линейная, обратная пропорциональность, степенная, квадратичная, кубическая, тригонометрические, логарифмическая и показательная.

Вторая глава позволяет рассматривать простейшие преобразования графиков такие как параллельный перенос и сдвиг . Эти преобразования часто встречаются в школьном курсе математики также очень часто встречаются в повседневной жизни.

Третья глава выпускной квалификационной работы представлена методической разработкой рабочей тетради по теме «Построение графиков элементарных функций», которая разработана для учащихся 9-11 классов. В ней содержится занятия на каждую тему, т.е. «линейная функция», «степенная функция», «Показательная функция» «логарифмическая функция» «тригонометрические функции». В начале каждой темы учащимся предлагается теоретический материал. Далее подробно разобраны несколько задач на данную тему занятия. Затем предлагаются задания, которые учащиеся должны решить самостоятельно. Задания предлагаются по степени возрастания сложности по данной теме. Данная рабочая тетрадь позволяет каждому учащемуся работать в индивидуальном темпе, а также помогает учащимся сформировать знания, умения и навыки самостоятельно.

Поставленные задачи определили структуру дипломной работы.

Глава 1. Общие сведения об элементарных функциях

1.1    Функция и ее свойства

Впервые определение функции было дано русским математиком Н.И.Лобачевским.

Термин «функция» введен Лейбницем, а символическая запись функциональной зависимости  впервые введена Л.Эйлером. Исторически первым способом задания функции был способ аналитический - при помощи формулы.

Понятие функции часто встречается в школьном курсе математики и хорошо знакомо учащимся. Рассмотрим это понятие.

Пусть D и E - непустые числовые множества, а х и у соответственно их элементы. Если каждому хD ставится в соответствие по некоторому закону только одно значение уE, то говорят, что между переменными х и у существует функциональная зависимость, и называют х - независимой переменной (или аргументом), а у - зависимой переменной (или функцией).

Для обозначения функций обычно пользуются буквами.

Символическая запись функции: y=f(x) (хD).

Хотя именно буква f связана со словом «функция», но для обозначения функциональной зависимости может применяться и любая другая буква.

Определение 1. Множество D называют областью определения функции и обозначают D(f), а множество E называют областью изменения функции. Говорят еще, что функция f отображает множество D на множество E.

Определение 2. Переменная величина y называется функцией переменной величины x, если каждому значению x соответствует определенное значение y.

Определение 3. Значение переменной х, при котором функция обращается в нуль, то есть f(x) = 0 называется нулём (или корнем) функции.

Определение 4. Функция у=f(x) называется чётной, если при изменении знака у аргумента значение функции не меняется: f(-x)=f(x). График чётной функции симметричен относительно оси ОY.

Определение 5. Функция у=f(x) называется нечётной, если при изменении знака у аргумента изменяется только знак значения функции: f(-x) = - f(x). График нечётной функции симметричен относительно начала координат.

Определение 6. Функция у=f(x) называется периодической, если существует такое постоянное число Т ≠ 0, что f(x+Т) = f(x). Наименьшее положительное число Т называют периодом.

Определение 7. Функция у=f(x) называется возрастающей, если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2).

Определение 8. Функция у=f(x) называется убывающей функцией, если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2).

График функции - это линия, дающая цельное представление о характере изменения функции по мере изменения ее аргумента. А именно, график функции y=f(x)  <#"531488.files/image003.gif"> - линейная;

 - обратная пропорциональность;

 - степенная;

;

 - квадратичная;

, кубическая;

 - тригонометрические;

 - логарифмическая;

 - показательная.

Графики некоторых из перечисленных функций можно построить, проведя исследование по заданной формуле, но этот процесс довольно трудоемкий и требует знаний дифференциального исчисления.

Во многих случаях графики элементарных функций можно построить по графику заданной его части или по графику другой функции с помощью линейных преобразований: параллельного переноса, растяжения (сжатия), преобразования симметрии.

1.2 Общая схема исследования функции и построения ее графика

. Элементарное исследование:

) найти область определения функции;

) исследовать функцию на симметричность и периодичность;

) вычислить предельные значения функции в ее граничных точках;

) выяснить существование асимптот;

) определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями;

) сделать эскиз графика функции, используя полученные результаты.

П. Исследование графика функции по первой производной:

) найти решение уравнений y’(х)=0 и y’(х)=¥ ;

) точки, “подозрительные” на экстремум, исследовать с помощью достаточного условия экстремума, определить вид экстремума;

) вычислить значения функции в точках экстремума;

) найти интервалы монотонности функции;

) нанести на эскиз графика экстремальные точки;

) уточнить вид графика функции согласно полученным результатам.

Ш. Исследование графика функции по второй производной:

) найти решения уравнений y”(х)=0 и y”(х)= ¥ ;

) точки, “подозрительные” на перегиб, исследовать с помощью достаточного условия;

) вычислить значения функции в точках перегиба;

) найти интервалы выпуклости и вогнутости графика функции;

) нанести на эскиз графика точки перегиба;

) окончательно построить график функции.

Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.

1.3 Графики элементарных функций

.3.1 Линейная функция y = kx + b

1.      Областью определения линейной функции служит множество R всех действительных чисел, так как выражение kx+b имеет смысл при любых значениях x.

2.      Множеством значений линейной функции при k¹0 является множество R всех действительных чисел.

.        Функция не является периодической, за исключением частного случая, когда функция имеет вид y=b.

.        Асимптоты графика функции не существуют.

.        Функция возрастает при k>0, функция убывает при k<0.

.        Функция не является ограниченной.

.        График линейной функции y=kx+b - прямая линия. Для построения этого графика, достаточно двух точек, например A(0; b) и B(-b/k; 0), если k¹0. График линейной функции y=kx+b может быть также построен с помощью параллельного переноса графика функции y=kx. Коэффициент k характеризует угол, который образует прямая y=kx и положительное направление оси Ox, поэтому k называется угловым коэффициентом. Если k>0, то этот угол острый, если k<0 - тупой; а при k=0 прямая параллельна оси Ox.

.        Точек перегиба не существует.

10.    Не существует экстремальных точек.

 =kx+b (k<0) y=kx+b (k>0)

1.3.2 Степенная функция y=xn

1. Область определения функции: D(f)= R;

. Область значений: E(f)= (0;+∞);

3. Функция является четной, т.е. f(-x)=f(x);

. Нули функции: y=0 при x=0;

5. Функция убывает при x(-∞;0];

. Функция возрастает при x[0;+ ∞);

7.      a) нет вертикальных асимптот

b) нет наклонных асимптот

. Если n-четное, то экстремум функции x=0

Если n-нечетное, то экстремумов функции нет

. Если n-четное, то точек перегиба нет

Если n-нечетное, то точка перегиба x=0

. График функции:

a) Если n=2, то графиком функции является квадратная парабола;

b) Если п = 3, то функция задана формулой у = х3. Ее графиком является кубическая  парабола;

c) Если п - нечетное натуральное число,причем п 1, то функция обладает свойствами теми же, что и у = х3.

Рассмотрим свойства степенной функции с нечетным показателем (п1):

1. Область определения функции: D(f)= R;

2. Область значений [0,+?];

. Функция является четной, т.е. f(-х)=f(х);

. Нули функции:у = 0 при х = 0;

. Функция убывает на промежутке (-?;0), возрастает на промежутке (0;+?).

. График функции:[рис.3]

Рассмотрим свойства степенной функции с четным показателем:

1. Область определения функции: D(f)= R;

2. Область значений: E(f)= R;

. Функция является нечетной, т.е. f(-х)=-f(х);

. Нули функции:у = 0 при х = 0;

. Функция возрастает на всей области определения.

. График функции:[рис.2]

1.3.3 Показательная функция у = ax

1.      Область определения функции: -? < х < +?

2.      Множество значений функции: 0 < y < +?

3.      Функция ни четная, ни не чётная, так как f(-x) = a-x

4.      Функция не является периодической.

5.      Асимптоты графика функции:

а) вертикальных асимптот не существует,

б) горизонтальная асимптота у = 0

6.      Если а > 1, то функция возрастает на промежутке -? < x < +? (рис.4);

7.      Если 0 < a < 1, то функция убывает на промежутке -? < x < +? (рис. 5);

8.      Точка (0; 1) - единственная точка пересечения с осями координат.

9. Не существует точек перегиба.

10. Не существует экстремальных точек.

Рис.4                                               Рис.5

1.3.4 Логарифмическая функция у = logax

1.     Область определения функции: 0 < x < ?

2.      Множество значений функции: -? < y < +?

.        Функция ни четная, ни нечетная, так как f(-x) = loga(-x)

.        Функция не периодическая

.        Асимптоты графика функции:

а) вертикальные асимптоты х = 0

б) горизонтальных асимптот не существует

6.                  Если a > 1, то функция возрастает на промежутке 0 < x < +? (рис.6);

если 0 < a < 1, то функция убывает на этом же промежутке (рис.7);

.                    Точка (1; 0) - единственная точка пересечения с осями координат.

8.Не существует точек перегиба.

.Не существует экстремальных точек.

1.3.5 Тригонометрические функции

Функция y=sin x

Свойства функции y=sin x:

2.     Область значений: E(f)=[-1;1];

3.      Функция является нечетной, т.е. sin(-x) = - sin x;

.        Функция периодическая с положительным наименьшим периодом 2π;

5.      Нули функции: sin x = 0 при x = πk, kZ;

.        Функция принимает положительные значения: sin x>0 при x(2πk;π+2πk), kZ;

.        Функция принимает отрицательные значения: sin x<0 при x(π+2πk;2π+2πk), kZ;

.        Функция возрастает на [-1;1] при x[ -+2πk;+2πk], kZ;

.        Функция убывает на [1;-1] при x[+2πk;+2πk], kZ;

.        Функция принимает наибольшее значение, равное 1, в точках x=+2πk, kZ;

.        Функция принимает наименьшее значение, равное -1, в точках x=+2πk, kZ;

12.    a) нет вертикальных асимптот

b) нет горизонтальных асимптот

13. Графиком функции является синусоида.

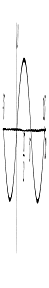
Функция y=cos x

Свойства функции y=cos x:

1. Область определения функции: D(f)=R;

2. Область значений: E(f)=[-1;1];

3. Функция является четной, т.е. cos (-x) = cos x;

4. Функция периодическая с наименьшим положительным периодом 2π;

Нули функции: cos x = 0 при x = +πk, kZ;

Функция принимает положительные значения: cos x>0 при x( -+2πk; +2πk), kZ;

Функция принимает отрицательные значения: cos x<0 при x( +2πk;+2πk), kZ;

Функция возрастает на [-1;1] при x[ -π+2πk;2πk], kZ;

Функция убывает на [1;-1] при x[2πk;π+2πk], kZ;

Функция принимает наибольшее значение, равное 1, в точках x=2πk, kZ;

Функция принимает наименьшее значение, равное -1, в точках x=π+2πk, kZ;

1. a) нет вертикальных асимптот

b) нет горизонтальных асимптот

2. Графиком функции является косинусоида:

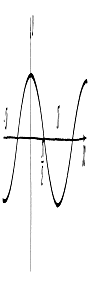
Функция y=tg x

Свойства функции y=tg x:

Область определения функции: D(f)=R , кроме чисел вида x =+πk, kZ;

1. Область значений: E(f)=R;

2. Функция является нечетной, т.е. tg (-x) = - tg x;

3. Функция периодическая с наименьшим положительным периодом π;

Нули функции: tg x = 0 при x = πk, kZ;

Функция принимает положительные значения: tg x>0 при x( πk; +πk), kZ;

Функция принимает отрицательные значения: tg x<0 при x( -+πk;πk), kZ;

Функция возрастает на (-;+?) при x(-+πk ;+πk ), kZ;

a) вертикальные асимптоты x= + πn

b) наклонных асимптот нет

1. Графиком функции является тангенсоида:

Функция y=ctg x

Свойства функции y=ctg x:

Область определения функции: D(f)=R , кроме чисел вида x = πn , где n Z;

1. Область значений: E(f)=R;

2. Функция является нечетной, т.е. ctg (-x) = - ctg x;

3. Функция периодическая с наименьшим положительным периодом π;

Нули функции: ctg x = 0 при x = +πn, nZ;

Функция принимает положительные значения: ctg x>0 при x( πn; +πn), nZ;

Функция принимает отрицательные значения: ctg x<0 при x( +πn;π +πn), nZ;

Функция убывает в каждом из промежутков (πn ;