Качественное исследование модели парения птиц в воздухе

Министерство образования и науки Российской Федерации

Агентство по образованию и науке Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

"Ижевский государственный технический университет"

факультет "Прикладная математика"

кафедра "Математическое моделирование процессов и технологий"

Курсовая работа

По дисциплине "Дифференциальные уравнения"

Тема: "Качественное исследование модели парения птиц в воздухе".

Руководитель работы:

доцент кафедры ММПТ: Т.М. Сидорик

Выполнил:

Студент гр.5-04-1: А.И. Егоров

Ижевск 2007

Оглавление

1. Введение

2. Качественное исследование модели парения птиц в воздухе

2.1 Основные понятия и определения

2.2 Построение модели

2.3 Исследование модели на устойчивость при отсутствии силы сопротивления воздуха

2.4 Нахождение траектории полета птицы (на примере планера) при отсутствии сопротивления воздуха

2.5 Исследование модели на устойчивость при наличии силы сопротивления воздуха

Заключение

Список литературы

1. Введение

Один из первопроходцев в теоретической и экспериментальной аэродинамике в России является Жуковский Н.Е. В этой науке он является родоначальником самых основных, самых драгоценных идей, которыми до сих пор руководствуются и учёные и инженеры. Н.Е. Жуковский начал интересоваться теорией авиации с 90-х годов прошлого столетия. При кабинете прикладной механики Московского университета уже с 1889 г. производились исследования по различным вопросам воздухоплавания: испытывались различные модели летательных машин и строились небольшие аэродинамические аппараты. В первой работе Н.Е. Жуковского по аэродинамике, опубликованной им в 1892 г., исследуется вопрос о планирующем полёте (парении) птиц, т.е. таком полёте, когда птица не машет крыльями. Н.Е. Жуковский разбирает два случая планирующего полёта: планирование с потерей высоты, или скольжение птицы по воздуху, и планирование с сохранением или даже набором высоты. Планирующий полёт птицы можно приближённо истолковать как движение пластинки под постоянным углом атаки. Подъёмную силу пластинки и её сопротивление Н.Е. Жуковский заимствует из экспериментов. Составив уравнения движения центра тяжести птицы, он находит его траектории при различных условиях движения воздуха. Среди возможных траекторий им была найдена траектория в виде "мёртвой петли". Таким образом, Н.Е. Жуковский теоретически предсказал возможность осуществления "мёртвой петли" за 11 лет до того, как первый самолёт братьев Райт поднялся в воздух.

1.      Постановка задачи

1.       Подобрать и изучить литературу по теме "Качественное исследование модели парения птиц в воздухе".

2.       Разобраться с основными понятиями и определениями.

.        Изучить основные этапы построения модели парения птиц в воздухе.

.        Разобраться в качественном исследовании модели парения птиц в воздухе.

5.       Рассмотреть конкретный пример.

.        Сделать выводы по работе.

2. Качественное исследование модели парения птиц в воздухе

2.1 Основные понятия и определения

Предельный цикл - замкнутая фазовая траектория С, имеющая окрестность из обыкновенных точек, в которой все фазовые траектории спиралевидно приближаются к С (устойчивый предельный цикл), или удаляются от С (неустойчивый предельный цикл), или приближаются к С с одной стороны и удаляются от нее с другой (полуустойчивый предельный цикл).

Признак Дюляка. Пусть дана дифференциальная система вида:

где X и Y непрерывны вместе со своими частными производными. Тогда, если существует непрерывная вместе с непрерывными частными производными функция B (x,y) такая, что в некоторой области G фазовой плоскости функция

является функцией знакоопределенной, то в области G нет предельных циклов данной дифференциальной системы.

Сепаратриса (от лат. separator - отделитель) - кривая, которая отделяет одно семейство интегральных кривых на фазовой плоскости от другого.

Фазовая плоскость. Положим x=y и будем изучать движение гармонического осциллятора, изображая это движение на плоскости x, y, где x и y - прямоугольные декартовы координаты. Каждому состоянию нашей системы, каждой паре значений координаты x и скорости y соответствует точка на плоскости x, y. Обратно каждой точке на плоскости x, y соответствует одно и только одно состояние системы. Плоскость x, y носит название плоскости состояний или, иначе, фазовой плоскости; она изображает совокупность всех возможных состояний нашей системы.

2.2 Построение модели

Чтобы построить математическую модель парения птицы в воздухе, рассмотрим задачу Н.Е. Жуковского о планирующем полете планера (самолета с выключенным мотором, птицы), происходящем в вертикальной плоскости (x, z) (в плоскости (x, z) ось Oz направлена вертикально вверх, а ось Ox - горизонтально таким образом, чтобы направление вектора начальной скорости с этой осью составляло острый угол). Полет птицы рассматривается при следующих предположениях:

) сила сопротивления воздуха пропорциональна квадрату скорости полета планера;

) угол атаки планера (угол между продольной осью планера и траекторией его центра тяжести) остается постоянным независимо от режима полета.

Введем обозначения: Пусть θ - угол наклона траектории планера (угол между касательной к траектории планера и осью Ox), v - скорость центра масс планера, т - масса планера, F - площадь его крыльев, g - ускорение силы тяжести, ρ - плотность воздуха, С₁ - аэродинамический коэффициент силы сопротивления воздуха, С₂ - аэродинамический коэффициент подъемной силы крыльев планера (рис. 2.2.1). При сделанном предположении о неизменности угла атаки планера аэродинамические коэффициенты С1 и С2 будут постоянными.

Рис. 2.2.1 Силы действующие на планер

На основании второго закона Ньютона уравнение движения центра масс планера в проекции на касательную к его траектории имеет вид

, (2.2.1)

где  - проекция силы тяжести;  - сила сопротивления воздуха. Уравнение движения центра масс планера в проекции на нормаль к траектории (уравнение движения для центростремительной компоненты ускорения) запишется в виде

, (2.2.2)

где  - величина подъемной силы планера; R - радиус кривизны траектории в рассматриваемой точке. Так как

, (2.2.3)

где  - угловая скорость движения центра масс планера, то из (2.2.2), (2.2.3) находится

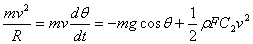. (2.2.4)

В уравнениях (2.2.1), (2.2.4) производится замена

, где

есть та скорость горизонтального полета планера, при которой вес планера уравновешивается подъемной силой. Кроме того, вводится новое время

.

Тогда из (2.2.1), (2.2.4) находится

, ,

а значит, уравнения движения запишутся в виде

 (2.2.5)

где a=C₁/C₂.

модель парение птица траектория

2.3 Исследование модели на устойчивость при отсутствии силы сопротивления воздуха

Точки M' (θ, y) и M" (θ+2π, y) соответствуют одному и тому же состоянию системы (2.2.5), т.к. при замене θ на θ+2π система (2.2.5) не изменяется. Последнее означает, что указанные точки естественно отождествлять и в качестве фазового пространства системы (2.2.5) рассматривать не плоскость (θ, у), а цилиндр, на котором вдоль образующей откладывается значение у, а вдоль направляющей - угол θ.

Кроме фазового кругового цилиндра, исследуется также развертка этого цилиндра на плоскость. При этом будут отождествляться точки граничных прямых развертки цилиндра, так как точки граничных прямых с одинаковыми у соответствуют одним и тем же состояниям системы. В цилиндрическом фазовом пространстве динамическая система исследуется обычным образом. Как и для случая фазовой плоскости, на поверхности цилиндра рассматриваются особые точки, сепаратрисы и предельные циклы, охватывающие состояния равновесия и соответствующие периодическим решениям системы. Однако на фазовом цилиндре, помимо предельных циклов, лежащих на поверхности цилиндра и окружающих состояния равновесия, но не охватывающих самого цилиндра (такие кривые вполне аналогичны замкнутым траекториям на фазовой плоскости), может встретиться совершенно новый тип предельных циклов, окружающих не состояния равновесия, а самый цилиндр. Очевидно, что и эти замкнутые кривые соответствуют периодическим решениям системы.

Уравнения замкнутых кривых, охватывающих цилиндр, можно записать в виде

где f (θ) является 2π-периодической функцией.

Для системы (2.2.5) будет исследоваться лишь область у≥0. Этим самым исключается случай полета планера "хвостом вперед".

Исключением в системе (2.2.5) d (τ), получается дифференциальное уравнение вида

. (2.3.1)

Уравнение (2.3.1) определяет интегральные кривые на поверхности цилиндра и имеет решение

. (2.3.2)

Прямая (2.3.2) является особой фазовой траекторией системы (2.2.5) и соответствует мгновенному опрокидыванию планера из положения θ=π/2 в положение θ= - π/2 при v=0 (согласно (2.2.5) при у=0, 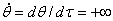, если  и , если ). В случае а=0, когда силы сопротивления отсутствуют уравнения движения примут вид

 (2.3.3)

Уравнение интегральных кривых (2.3.1) в этом случае будет таким:

 (2.3.4)

Особые точки уравнения (2.3.4) находятся из системы

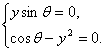 (2.3.5)

Решениями системы (2.3.5) являются:

) θ=0, у=1;

) θ=π/2, у=0;

) θ= - π/2, у=0.

Состоянием равновесия системы (2.3.3) будет особая точка θ=0, у=1. Она соответствует режиму горизонтального полета планера с постоянной скоростью v=v₀. Особые точки θ=π/2, у=0 и θ= - π/2, у=0 лежат на особой прямой (2.3.2), соответствующей, как уже отмечалось, мгновенному опрокидыванию планера при v=0. Они не являются состояниями равновесия системы (2.3.3), так как в этих точках .

Уравнение (2.3.4) можно записать в виде

 (2.3.6)

Уравнение (2.3.6) является уравнением в полных дифференциалах, т.к.

Находится общий интеграл уравнения (2.3.6). Имеется

, а значит,

.

Далее находится

, т.е. . (2.3.7)

Из уравнения (2.3.7) получается

.

Таким образом, общий интеграл уравнения (2.3.6) имеет вид

. (2.3.8)

Если положить , то уравнение семейства кривых (2.3.8) можно записать в виде

. (2.3.9)

Далее исследуется семейство кривых (2.3.9). Находится

.

Следовательно, точки экстремума кривых (2.3.9) лежат на параболе η=у². Ясно, что  при . Таким образом, при С>0 имеется, что у_с<0. Если С≤0, то при у<у_c выполняется неравенство у²-η<0, а при у>у_c - неравенство у²-η>0, т.е. кривые (2.3.9) при у=y_c имеют минимумы (рис.2.3.1). При С= - 2/3 получается у_c=1, а значит, η_c=1, т.е. cos (θ) =1, θ=0. Итак, значению С= - 2/3 соответствует состояние равновесия θ=0, у=1 системы (2.2.5). При - 2/3<С<0 кривые семейства (2.3.9) расположены выше оси Оу, а при С<-2/3 они лежат целиком над прямой η=1. При любом фиксированном С>0 функция (2.3.9) является возрастающей на R₊= [0,+∞) функцией от у, принимающей все действительные значения. Ясно, что имеет смысл рассмотрение кривых (2.14) с |η|≤1.

Рис. 2.3.1 Графики функции η=η (y) при различных C

На развертке фазового цилиндра семейство кривых (2.3.8) (ясно, что θ=±arccos (η)) при - 2/3<C<0 представляет замкнутые траектории, охватывающие состояние равновесия θ=0, у=1 (рис. 2.3.2).

Рис. 2.3.2 Интегральные кривые на развертке фазового цилиндра

На фазовом цилиндре это семейство кривых, охватывающее состояние равновесия θ=0, у=1, не охватывает цилиндра (рис. 2.3.3).

Рис. 2.3.3 Интегральные кривые на фазовом цилиндре

Отсюда следует, что состояние равновесия θ=0, у=1 является центром для системы (2.2.5).

Семейство же кривых (2.3.8) при С>0 представляет замкнутые фазовые траектории, охватывающие цилиндр. На развертке цилиндра им соответствуют кривые, для которых у (-π) =у (π). При С=0 на фазовом цилиндре имеем

, (2.3.10)

разделяющую эти два типа замкнутых траекторий (см. рис. 2.3.3).

График уравнения (2.3.10) состоит из сепаратрис седел (θ=π/2, у=0 и θ= - π/2, у=0) системы

 (2.3.11)

Действительно, состояниями равновесия системы (2.3.11) при y≥0 являются A (0,1), В (π/2,0), C (-π/2,0). При y≠0 фазовые траектории систем (2.2.5) и (2.3.11) совпадают (им соответствует одно и то же уравнение интегральных кривых (2.3.4)), а поэтому особая точка А (0, 1) является центром для (2.3.11). Для исследования особой точки В (π/2,0) производится параллельный перенос

 .

В результате получается дифференциальная система вида

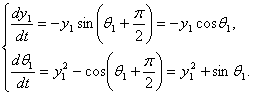 (2.3.12)

Для исследования особой точки O (0,0) системы (2.3.12) вычисляются дифференциалы функций sin (θ₁) и cos (θ₁) при θ₁=0. Имеется:

 а значит,

 где

.

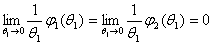Таким образом, систему (2.3.12) можно записать в виде

Характеристическим уравнением для соответствующей линеаризованной системы является:

.

Корни этого уравнения λ₁=1>0, λ₁= - 1<0, и, значит, особая точка В (π/2,0) системы (2.3.11) будет седлом. При этом сепаратрисы, касающиеся оси Oθ, являются отталкивающими, а сепаратрисы, касающиеся оси Оу, - притягивающими. Так как интегральные кривые систем (2.2.5) и (2.3.11) совпадают, то отсюда следует, что все они могут быть найдены из (2.3.8). При этом сепаратрисы седла В (π/2,0) определяются из уравнения (2.3.10), так как других интегральных кривых, проходящих через особую точку В, уравнение (2.3.4) не имеет. Из (2.3.10) находится, что y=0. Это отталкивающая сепаратриса седла В. Притягивающая сепаратриса при y>0 имеет вид

Аналогично исследуется особая точка C (-π/2,0). Таким образом, фазовые траектории системы (2.2.5) на развертке цилиндра и на самом фазовом цилиндре имеют вид, изображенный на рис. 2.3.3.

2.4 Нахождение траектории полета птицы (на примере планера) при отсутствии сопротивления воздуха

Рассмотрим теперь траектории полета планера в вертикальной плоскости (х, z) при отсутствии сопротивления воздуха. Проекция скорости v на ось Oz имеет вид

.

С другой стороны,

, т.е. .

Таким образом, из (2.2.1) при C₁=0 получается

,

 (2.4.1)

Интегрированием (2.4.1), находится

Полагая при z=0 v=0 (высота z отсчитывается от того уровня, которому при данных начальных условиях соответствует скорость планера v=0), имеется, что С=0, т.е.

. Отсюда . (2.4.2)

Далее находится соотношение между z и θ. Из (2.4.2) получается

. (2.4.4)

Подставлением (2.4.4) в (2.3.8), находится

. (2.4.5)

Согласно геометрическому смыслу производной,

.

Следовательно,

, (2.4.6)

где f (z, С) - функция, которая получается, если tg (θ) выразить через z при помощи соотношения (2.4.5). Интегрированием (2.4.6) (интеграл от правой части (2.4.6) в элементарных функциях не выражается), получается зависимость х от z. Если С=-2/3, то тогда cos (θ) =1,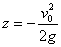, т.е. имеет место горизонтальный полет планера с постоянной скоростью v₀.

При С=0

, (2.4.7)

Дифференцированием (2.4.7) по x, находится

, т.е. .

Таким образом,

 . (2.4.8)

Исключением из соотношений (2.4.7), (2.4.8) переменной θ, получается уравнение окружности

.

Следовательно, случай С=0 соответствует полету планера по полуокружностям, радиус которых равен  (при этом исключаются точки, лежащие на оси Ох, так как в них мгновенное переворачивание планера физически невозможно).

При - 2/3<С<0 траектории полета планера имеют форму волнообразных линий (в этом случае 0<cos (θ) <l). Случай С>0 соответствует полету, при котором планер совершает "мертвые петли" (здесь - 1≤cos (θ) ≤1).

Различные траектории полета планера в вертикальной плоскости (х, z) изображены на рис. 2.4.1.

Рис. 2.4.1 Траектории полета планера при отсутствии сопротивления воздуха

Таким образом, движение изображающей точки по замкнутым фазовым траекториям, охватывающим состояние равновесия на фазовом цилиндре, соответствует полету планера по волнообразным линиям, а при движении по кривым, охватывающим фазовый цилиндр, - полету планера по "мертвым петлям".

2.5 Исследование модели на устойчивость при наличии силы сопротивления воздуха

Далее рассматривается полет планера при учете сопротивления воздуха С₁.

В этом случае состояния равновесия системы (2.2.5) находятся из системы уравнений

 (2.5.1)

откуда получается

 т.е.

Таким образом, система (2.2.5) имеет единственное состояние равновесия, координаты которого θ₀, y₀ определяются выражениями:

Это состояние равновесия соответствует полету планера по нисходящей прямой с постоянной скоростью v<v₀. Исследование состояния равновесия θ₀, y₀. производится путем параллельного переноса

приводящего систему дифференциальных уравнений (2.2.5) к виду

 (2.5.2)

Для выделения главных линейных членов системы (2.5.2) в окрестности начала координат находятся дифференциалы функций f1, f2 при u=φ=0. Имеется:

 (2.5.3)

С учетом (2.5.3) система (2.5.2) записывается в виде (следует положить du=u, d (φ) =φ)

где функции g1 (u,φ), g2 (u,φ) состоят из членов выше первого порядка.

Характеристическое уравнение для соответствующей линеаризованной системы имеет вид

Это уравнение с учетом (2.5.1) записывается так:

. (2.5.4)

Корнями характеристического уравнения (2.5.4) являются числа

.

Таким образом, при  состояние равновесия θ₀, y₀ системы (2.2.5) является устойчивым фокусом, а при  - устойчивым узлом.

Далее проверяется отсутствие предельных циклов. Для этого используется критерий Дюляка. В качестве функции Дюляка берется функция В (θ, у) =у. Для системы (2.2.5) получается

.

Это выражение обращается в нуль лишь на окружности y=0, охватывающей фазовый цилиндр. Следовательно, в области y>0 не существует замкнутых фазовых траекторий, не охватывающих фазовый цилиндр. Можно доказать, что в области y≥0, за исключением y=0, не может быть замкнутых траекторий, охватывающих фазовый цилиндр. Таким образом, система уравнений (2.2.5) в области y>0 не имеет предельных циклов, как охватывающих цилиндр, так и не охватывающих его. Иначе говоря, рассматриваемая система не имеет (при наличии сил сопротивления воздуха) никаких периодических колебательных движений.

Уравнение интегральных кривых (2.3.1), как и в случае а=0, имеет, кроме состояния равновесия М_о (θ₀, y₀), еще две особые точки М₁ (-π/2,0), М₂ (π/2,0), которые являются седлами.

Доказывается это аналогично случаю а=0. Однако теперь в отличие от случая а=0 можно доказать, что сепаратриса седла М1, выходящая на верхнюю половину фазового цилиндра, уже не может входить в седло М2. Так как при

,

то все фазовые траектории идут из далеких областей верхней половины цилиндра в область, заключенную между окружностями у=0 и  и содержащую в себе состояние равновесия М_о (θ₀,y₀). Принимая во внимание отсутствие замкнутых интегральных кривых (кроме окружности у=0), можно утверждать, что все фазовые траектории приближаются к устойчивому состоянию равновесия - к точке М_о (к ней, в частности, приближается и сепаратриса седла М₁ (-π/2,0). Таким образом, качественная картина разбиения фазового цилиндра на фазовые траектории системы (2.2.5) имеет вид, изображенный на рис. 2.5.1.

Рис. 2.5.1 Интегральные кривые на фазовом цилиндре

Итак, планер при наличии сопротивления воздуха имеет единственный устойчивый равновесный режим - полет с постоянной скоростью v=v_oy_o по нисходящей прямой, составляющей с горизонтом угол θ₀. Если начальная скорость планера достаточно велика (на фазовом цилиндре мы попадаем на фазовую траекторию, охватывающую несколько раз цилиндр.), то планер совершит сначала несколько "мертвых петель" и затем по волнообразно затухающей траектории приблизится к траектории прямолинейного полета. Одна из возможных траекторий полета планера показана на рис.2.5.2.

Рис. 2.5.2 Одна из возможных траекторий полета планера

3. Пример

Определим данные полета g, ρ, F, m, C_1, C₂ и найдем траекторию планирующего полета на примере черного коршуна: g=9,8 м/с² - ускорение свободного падения; ρ=1,29 кг/м³ - плотность воздуха; F=0,5 м² - площадь крыльев коршуна; m=1 кг - масса коршуна; C₁=0,05 - аэродинамический коэффициент силы сопротивления воздуха; C₂=0,7 - аэродинамический коэффициент подъемной силы крыльев коршуна.

Коэффициенты C₁ и C₂ определяются из зависимостей представленных на рис. 3.1, при условии, что угол атаки равен нулю. Полет происходит при наличии силы сопротивления воздуха, т.к. коэффициент C₁ не равен нулю

Рис. 3.1 Зависимость аэродинамических коэффициентов C₁ и C₂ от угла атаки крыла

Потом исследуем систему дифференциальных уравнений (2.2.1), (2.2.4) на устойчивость:

 (3.1)

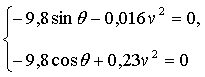
Решаем данную систему:

,

Таким образом система имеет состояние равновесия, координаты которого θ₀=-4,004 v₀=6,54. Исследуем состояние равновесия θ₀=-4,004 v₀=6,54. Параллельный перенос

приводит систему дифференциальных уравнений (3.1) к виду

 (3.2)

Найдем дифференциалы функций f1, f2 при u=φ=0:

 (3.3)

С учетом (3.3) система (3.2) записывается в виде (следует положить du=u, d (φ) =φ)

где функции g1 (u,φ), g2 (u,φ) состоят из членов выше первого порядка.

Решая полученное характеристическое уравнение

.

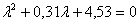получаем корни

Т.к. действительная часть корней меньше 0, то состояние равновесия θ₀=4,004 v₀=6,54 системы (3.1) является устойчивым фокусом.

Заключение

В ходе проделанной курсовой работы мной была подобрана и изучена литература по теме качественное исследование модели парения птиц в воздухе, а также я познакомился с моделью парения птиц в воздухе на примере планирующего полета планера. В результате исследования на устойчивость данной модели было выяснено, что ее решение является устойчивым как в случае отсутствия, так и при наличии сопротивления воздуха. В первом случае птица будет лететь либо по волнообразной траектории (иногда с "мертвыми петлями"), либо по прямой горизонтальной линии. Во втором случае его траектория более реалистичная и представляет собой после стабилизации нисходящую прямую линию.

Список литературы

1.       Жуковский, Н.Е. "Избранные сочинения". - М.: Государственное издательство технико-теоретической литературы, 1948. - Т.2.

2.       Камке, Э. "Справочник по обыкновенным дифференциальным уравнениям". - М.: Наука, 1977.

3.       Несущие крылья (профиль крыла) /<http://www.rcdesign.ru/articles/avia/wings_profile>

.        Амелькин, В.В., Садовский А.П. "Математические модели и дифференциальные уравнения". - Минск: Высшая школа, 1982.

.        Агафонов С.А. "Дифференциальные уравнения", Москва, 2000

.        Двайт, Г.Б. "Таблицы интегралов и другие математические формулы". - М.: Наука, 1978

.        Богданов Ю.С. "Лекция по дифференциальным уравнениям." - Минск.: Высшая школа, 1997

.        Еругин Н.П. "Книга для чтения по общему курсу дифференциальных уравнений." - Минск.: Наука и Техника, 1977

.        Корн, Г., Корн Т. "Справочник по математике для научных работников и инженеров." - М.: Наука, 1984

.        Жуковский, Н.Е. "Полное собрание сочинений. Теоретические основы воздухоплавания." - М.: Главная редакция авиационной литературы, 1938.