|
БП
|
Своб. члены
|
НП
|
|
|
x7
|
X1
|
|
x2
|
6
|
1
|
0
|
|
x4
|
9
|
4
|
-1
|
|
x5
|
30
|
18
|
-8
|
|
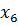
|
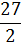
|
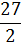
|
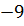
|
|
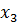
|
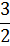
|
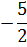
|
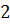
|
|
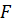
|
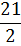
|
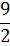
|
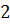
|
Решение является оптимальным и допустимым.
Из симплекс-таблицы 2.7 получаем:
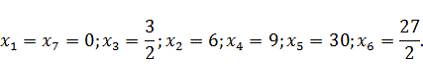 (2.13)
(2.13)
В
исходную функцию цели и ограничения входят только переменные 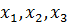
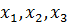 , поэтому
оптимальный план решения задачи:
, поэтому
оптимальный план решения задачи:
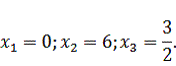 (2.14)
(2.14)
Экстремальное значение функции (2.1) примет значение:
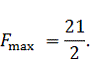
Таким
образом, найденное оптимальное решение соответствует требованию целочисленного
значения переменной 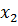
 .
.
3. Нелинейное программирование
.1 Нахождение безусловного экстремума функции F(x)
Исходная задача имеет вид:
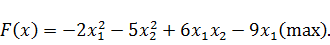
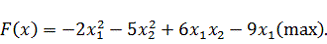 (3.1)
(3.1)
Начальная точка имеет координаты: 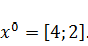
График функции, построенный в Matlab, представлен на рисунке 3.1.
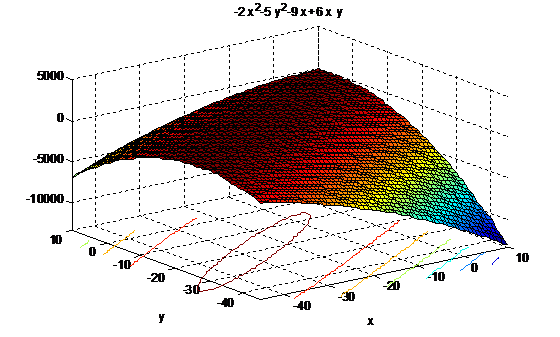
Рисунок 3.1 - График функции в Matlab
Решим задачу различными методами и сравним полученные результаты.
Метод Ньютона-Рафсона.
В
данном методе решение заданной нелинейной задачи, как правило, происходит за
один шаг, т.е. 
 будет
решением данной задачи.
будет
решением данной задачи.
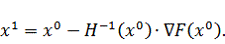
Здесь
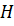
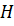 -
матрица Гессе (матрица, составленная из вторых частных производных),
-
матрица Гессе (матрица, составленная из вторых частных производных), 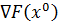
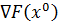 -
значение градиента функции в начальной точке.
-
значение градиента функции в начальной точке.
Найдем
вид вектора градиента:
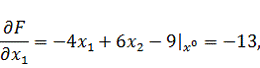
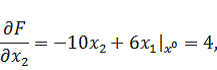
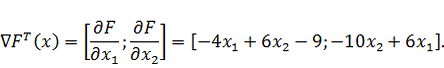 (3.2)
(3.2)
В
точке 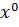
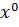 вектор
градиента примет значение:
вектор
градиента примет значение: 
Составим матрицу Гессе:
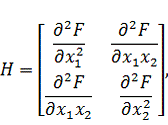
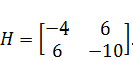
Найдем обратную матрицу для матрицы Гессе.
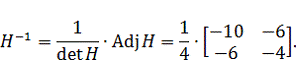
Координаты следующей точки будут определятся по выражению:
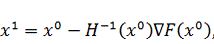
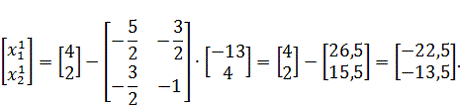
Найдем
значение вектора градиента по выражению (3.2) в точке 
 :
:
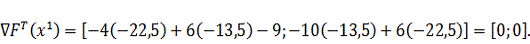
Следовательно
в точке 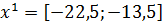
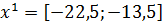 функция
достигает своего максимального значения:
функция
достигает своего максимального значения:
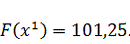
Метод наискорейшего спуска
В данном методе на каждой итерации в текущей точке определяется
направление движения (вектором градиента для задачи на максимум) и величина
шага в данном направлении [2].
Шаг 1.
Координаты
точки 
 будут
определяться выражением:
будут
определяться выражением:
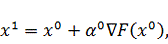
где
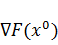
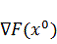 -
значение вектора градиента, вычисленное в точке
-
значение вектора градиента, вычисленное в точке 
 ;
;
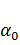
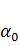 -
величина шага в данном направлении.
-
величина шага в данном направлении.
Найдем
значение функции по выражению (3.1) в точке 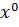
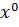 :
: 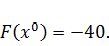
Найдем
направление вектора градиента по выражению (3.2) в точке 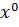
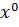 :
: 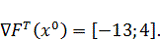
Подставим известные значения в выражение для определения координаты
следующей точки:
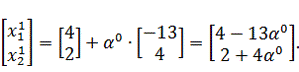
Найдем
величину шага 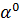
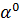 . Для
этого подставим в функцию (3.1) найденные выражения для
. Для
этого подставим в функцию (3.1) найденные выражения для 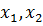
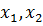 , т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум, для чего возьмем производную от полученной функции и приравняем к
нулю:
, т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум, для чего возьмем производную от полученной функции и приравняем к
нулю:
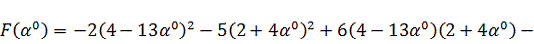
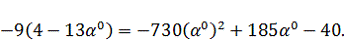
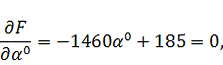
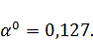
Тогда
координаты точки 
 будут
равны:
будут
равны:
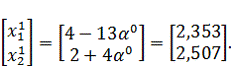
Найдем
значение функции по выражению (3.1) в точке 
 :
: 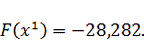
Шаг 2.
Координаты
точки 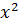
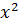 будут
определяться выражением:
будут
определяться выражением:
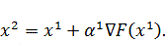
Найдем
направление вектора градиента по выражению (3.2) в точке 
 :
:
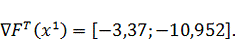
Подставим известные значения в выражение для определения координаты
следующей точки:
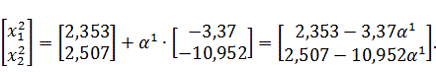
Найдем
величину шага 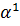
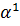 . Для
этого подставим в функцию (3.1) найденные выражения для
. Для
этого подставим в функцию (3.1) найденные выражения для 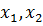
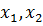 , т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум:
, т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум:
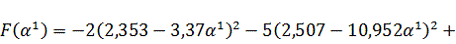
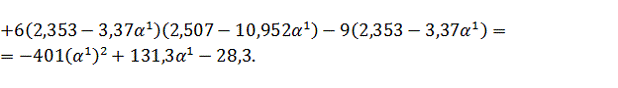
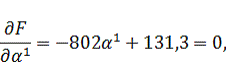
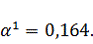
Тогда
координаты точки 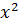
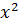 будут
равны:
будут
равны:
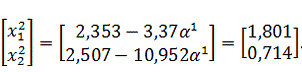
Найдем
значение функции по выражению (3.1) в точке 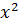
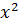 :
:
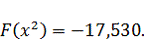
Шаг 3.
Координаты
точки 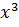
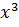 будут
определяться выражением:
будут
определяться выражением:
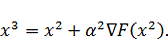
Найдем
направление вектора градиента по выражению (3.2) в точке 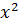
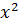 :
:
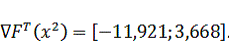
Подставим известные значения в выражение для определения координаты
следующей точки:

Найдем
величину шага 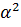
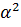 :
:
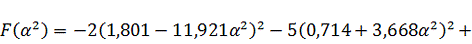
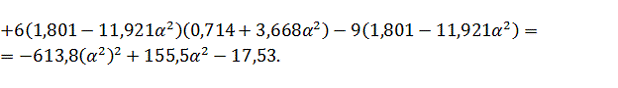
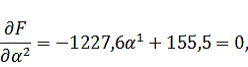
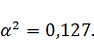
Тогда
координаты точки 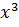
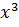 будут
равны:
будут
равны:
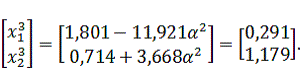
Найдем
значение функции по выражению (3.1) в точке 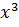
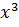 :
:
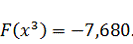
Шаг 4.
Координаты
точки 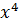
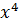 будут
определяться выражением:
будут
определяться выражением:
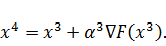
Найдем
направление вектора градиента по выражению (3.2) в точке 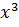
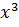 :
:
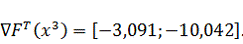
Подставим известные значения в выражение для определения координаты
следующей точки:
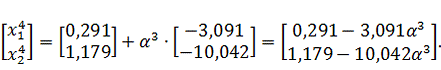
Найдем
величину шага 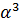
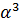 :
:
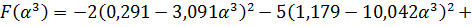
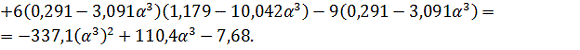
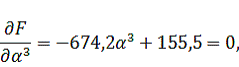
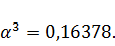
Тогда
координаты точки 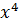
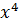 будут
равны:
будут
равны:
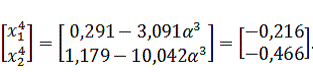
Найдем
значение функции по выражению (3.1) в точке 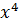
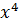 :
:
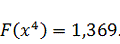
Графическая интерпретация метода найскорейшего спуска представлена на
рисунке 3.2.
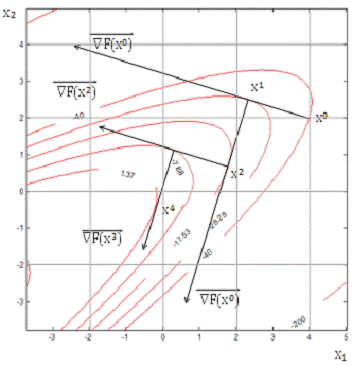
Рисунок 3.2 - Графическая интерпретация метода наискорейшего спуска
Метод наискорейшего спуска для данной функции медленно сходится к точному
решению, что видно из расчетов и рисунка.
3.2 Нахождение экстремума функции F(x) с учетом
системы ограничений
На задачу (3.1) наложим ограничения на значения переменных в соответствии
с условием. Полученная задача примет вид:
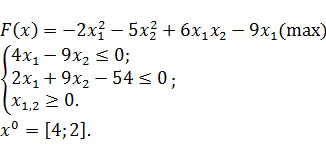
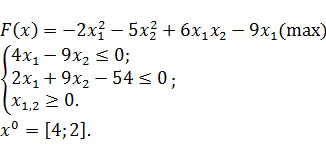 (3.3)
(3.3)
Для графического построения области определения преобразуем неравенства:
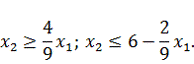
Область определения построена на рисунке 3.3.
Метод допустимых направлений Зойтендейка.
Метод Зойтендейка является расширением метода наискорейшего спуска,
позволяющий учитывать ограничения. На каждом шаге строится возможное допустимое
направление шага, и выбирается величина шага в соответствии с ограничениями
[1].
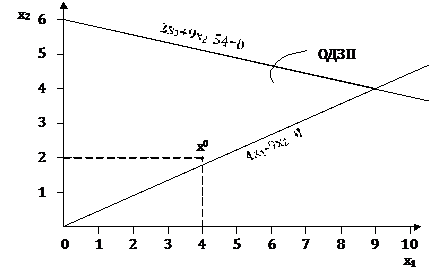
Рисунок 3.3 - Область допустимых значений переменных
Шаг 1.
Координаты
точки 
 будут
определяться выражением:
будут
определяться выражением:
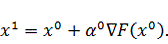
Найдем
направление вектора градиента по выражению (3.2) в точке 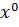
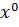 :
:
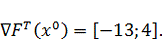
Подставим известные значения в выражение для определения координаты
следующей точки:
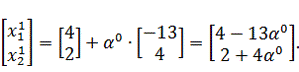
Найдем
величину шага 
 . Для
этого подставим в функцию (3.1) найденные выражения для
. Для
этого подставим в функцию (3.1) найденные выражения для 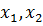
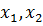 , т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум:
, т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум:
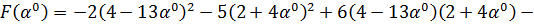
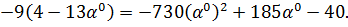
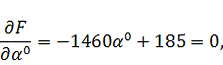
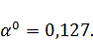
Найдем
интервал допустимых значений 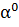
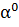 , который
обеспечивает нахождение точки внутри ОДЗП:
, который
обеспечивает нахождение точки внутри ОДЗП:
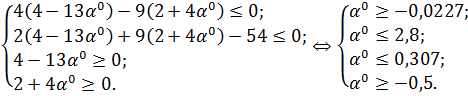
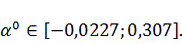
Найденное
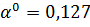
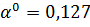 входит в
найденный выше интервал. Тогда координаты следующей точки определяться по
выражению:
входит в
найденный выше интервал. Тогда координаты следующей точки определяться по
выражению:
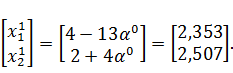
Шаг 2.
Координаты
точки 
 будут
определяться выражением:
будут
определяться выражением:
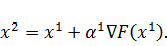
Найдем
направление вектора градиента по выражению (3.2) в точке 
 :
:
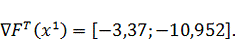
Подставим известные значения в выражение для определения координаты
следующей точки:
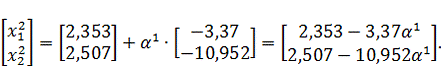
Найдем
величину шага 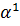
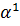 так же,
как и на предыдущих шагах:
так же,
как и на предыдущих шагах:
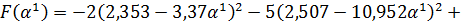
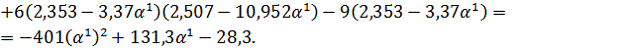
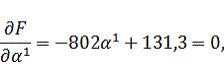
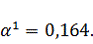
Найдем
интервал допустимых значений 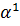
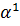 , который
обеспечивает нахождение точки внутри ОДЗП:
, который
обеспечивает нахождение точки внутри ОДЗП:
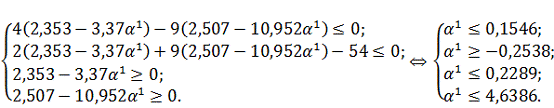
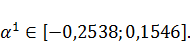
Найденное
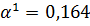
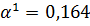 не
входит в найденный выше интервал. В качестве величины шага возьмем правую
границу интервала
не
входит в найденный выше интервал. В качестве величины шага возьмем правую
границу интервала 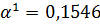
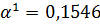 .
.
Найдем
координаты следующей точки:
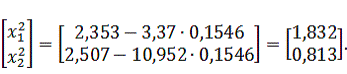
Шаг 3.
Найдем
направление вектора градиента по выражению (3.2) в точке 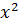
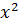 :
:
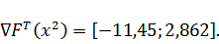
Вектор градиента направлен в сторону ОДЗП. Следовательно, координаты
следующей точки будут определяться по выражению:
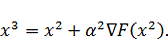
Подставим известные значения в выражение для определения координаты
следующей точки:
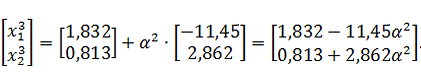
Найдем
величину шага 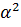
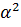 так же,
как и на предыдущих шагах:
так же,
как и на предыдущих шагах:
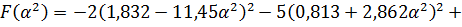
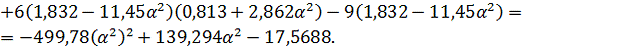
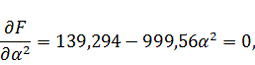
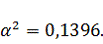
Найдем
интервал допустимых значений 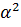
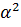 , который
обеспечивает нахождение точки внутри ОДЗП:
, который
обеспечивает нахождение точки внутри ОДЗП:
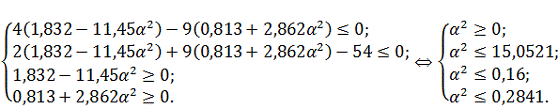
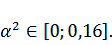
Найденное
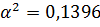
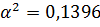 входит в
найденный выше интервал. Тогда координаты следующей точки определятся по
выражению:
входит в
найденный выше интервал. Тогда координаты следующей точки определятся по
выражению:
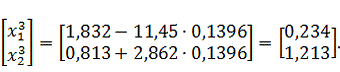
Шаг 4.
Координаты
точки 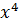
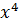 будут
определяться выражением:
будут
определяться выражением:
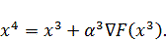
Найдем
направление вектора градиента по выражению (3.2) в точке 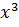
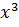 :
:
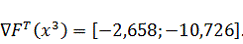
Подставим известные значения в выражение для определения координаты
следующей точки:
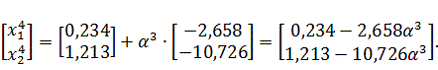
Найдем
величину шага 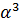
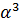 так же,
как и на предыдущих шагах:
так же,
как и на предыдущих шагах:
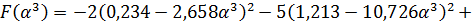
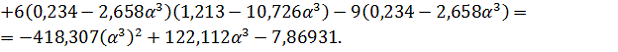
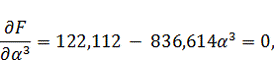
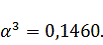
Найдем
интервал допустимых значений 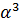
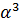 , который
обеспечивает нахождение точки внутри ОДЗП:
, который
обеспечивает нахождение точки внутри ОДЗП:
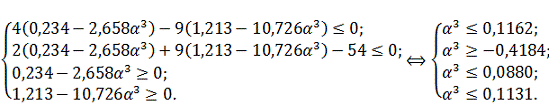
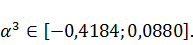
Найденное
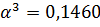
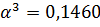 не
входит в найденный выше интервал. В качестве величины шага возьмем правую
границу интервала
не
входит в найденный выше интервал. В качестве величины шага возьмем правую
границу интервала 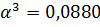
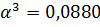 .
.
Найдем
координаты следующей точки:
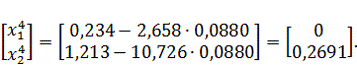
Шаг 5.
Найдем
направление вектора градиента по выражению (3.2) в точке 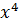
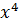 :
:
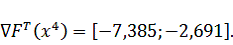
Вектор
градиента направлен за ОДЗП. Поэтому необходимо найти направление 
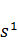 , в
сторону которого нужно двигаться. Найдем это направление из условия
, в
сторону которого нужно двигаться. Найдем это направление из условия 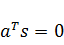
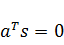 , где
, где 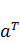
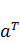 -
вектор, составленный из коэффициентов при переменных ограничения, на котором
находится точка. Так как точка
-
вектор, составленный из коэффициентов при переменных ограничения, на котором
находится точка. Так как точка 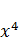
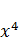 принадлежит
граничной прямой
принадлежит
граничной прямой 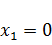
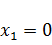 , то
направление
, то
направление 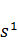
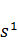 очередного
шага определяем из условия:
очередного
шага определяем из условия:
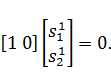
Отсюда
следует, что 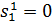
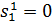 . Тогда
из условия нормировки:
. Тогда
из условия нормировки:
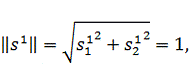
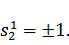
При
движении вдоль граничной прямой следует двигаться в направлении, которое
составляет острый угол с вектором градиента, т.е. скалярное произведение
векторов 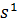
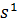 и
и 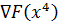
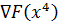 должно
быть больше или равно нуля [2]. Это достигается при выборе:
должно
быть больше или равно нуля [2]. Это достигается при выборе:
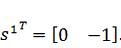
Координаты
точки 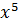
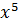 будут
определяться выражением:
будут
определяться выражением:
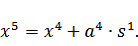
Подставим известные значения в выражение для определения координаты
следующей точки:
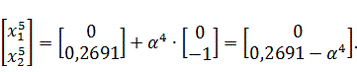
Найдем
величину шага 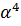
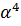 :
:
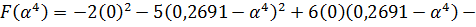
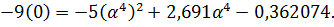
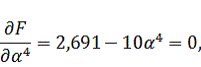
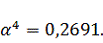
Найдем
интервал допустимых значений 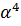
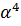 , который
обеспечивает нахождение точки внутри ОДЗП. Ограничение, вдоль которого
происходит движение, опускается:
, который
обеспечивает нахождение точки внутри ОДЗП. Ограничение, вдоль которого
происходит движение, опускается:
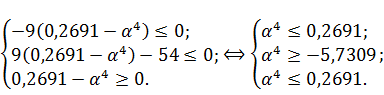
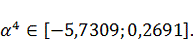
Найденное
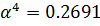
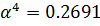 входит в
найденный выше интервал. Тогда координаты следующей точки определятся по
выражению:
входит в
найденный выше интервал. Тогда координаты следующей точки определятся по
выражению:
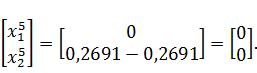
Найденная точка находится в вершине ОДЗП.
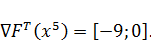
Проверим
перпендикулярность направления движения s1 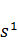 и вектора градиента
и вектора градиента 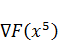
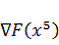 , для
этого перемножим эти вектора скалярно:
, для
этого перемножим эти вектора скалярно:
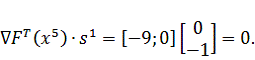
Скалярное произведение равно нулю, следовательно вектор градиента
перпендикулярен направлению движения, значит максимум достигнут.
Найдем
значение функции по выражению (3.1) в точке 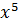
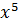 :
:
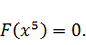
Графическая интерпретация задачи представлена на рисунке 3.4.
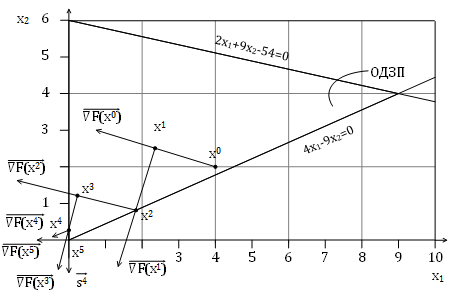
Рисунок 3.4 - Графическая интерпретация метода Зойтендейка
Метод Куна-Таккера.
Метод предназначен для решения задачи, в которой функция является
квадратичной, а все ограничения линейны.
Метод основан на использовании теоремы Куна-Таккера.
Функция Лагранжа имеет вид:
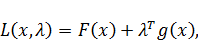
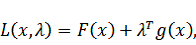 (3.3)
(3.3)
где
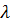
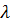 -
неопределенные множители Лагранжа;
-
неопределенные множители Лагранжа;
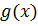
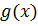 - левые
части ограничений задачи, приведенные к нулевой правой части.
- левые
части ограничений задачи, приведенные к нулевой правой части.
Условия
теоремы Куна-Таккера для задачи на поиск максимума:
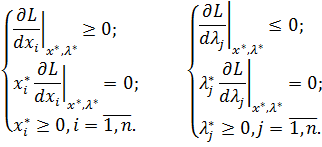 (3.4)
(3.4)
Преобразуем ограничения задачи к виду с нулевой правой частью. При этом
поскольку решается задача на поиск максимума, ограничения приводятся к знаку
больше или равно:
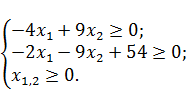
Составим функцию Лагранжа для задачи:
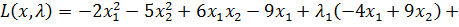
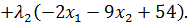 (3.5)
(3.5)
Составим систему уравнений в соответствии с выражением (3.4):
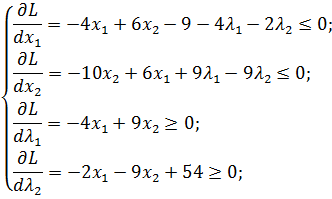 (3.6)
(3.6)
Приведем
ограничения задачи (3.6) к виду равенств, введя дополнительные переменные 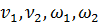
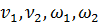 :
:
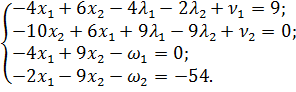 (3.7)
(3.7)
Для решения задачи линейного программирования (3.7) составим
симплекс-таблицу.
Таблица 3.1 - Исходная симплекс-таблица
|
БП
|
Своб. члены
|
НП
|
|
|
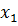
|
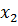
|
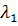
|
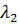
|
|
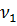
|
9
|
-4
|
6
|
-4
|
-2
|
|
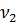
|
0
|
6
|
-10
|
9
|
-9
|
|
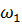
|
0
|
4
|
-9
|
0
|
0
|
|
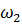
|
54
|
2
|
9
|
0
|
0
|
Решения является допустимым, так как все свободные члены положительны.
Из симплекс таблицы 3.1 получим:
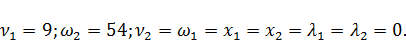
Параметрами
координаты искомой точки являются только 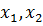
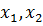 , поэтому
оптимальный план решения задачи:
, поэтому
оптимальный план решения задачи:
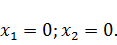
Искомая
точка экстремума 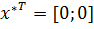
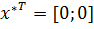 .
.
Решение
задачи методом Куна-Таккера совпадает с решением методом Зойтендейка.
Метод
линейных комбинаций.
В
данном методе на каждом шаге в предыдущей точке нелинейная функция цели
линеаризуется посредством разложения в ряд Тейлора в окрестности данной точки,
пренебрегая всеми степенями старше первой. Затем решается задача линейного
программирования, её решение будет в некоторой вершине ОДЗП. После этого
необходимо найти величину шага в направлении вершины и координаты следующей
точки [2].
Линеаризованная
функция имеет вид:
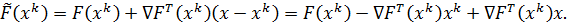
Здесь
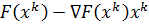
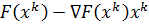 является
постоянной величиной, поэтому не оказывает влияние на максимизацию. Тогда можно
записать:
является
постоянной величиной, поэтому не оказывает влияние на максимизацию. Тогда можно
записать:
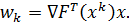
Решим
задачу (3.2) с помощью метода линейных комбинаций.
Шаг
1.
Начальная
точка: 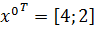
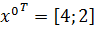 .
.
Найдем
направление вектора градиента по выражению (3.2) в точке 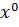
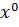 :
:
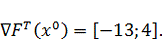
Составим
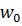 для
текущего шага:
для
текущего шага:
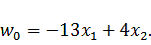
Решим
задачу линейного программирования:
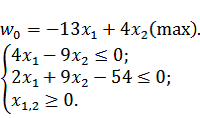
Для получения решения данной задачи составим симплекс-таблицу и решим ее
согласно правилам:
Таблица 3.2 - Первая итерация
|
БП
|
Своб. чл.
|
НП
|
|
|
x1
|
x2
|
|
x3
|
0
|
4
|
-9
|
|
x4
|
2
|
9
|
|
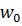
|
0
|
13
|
-4
|
Решение является допустимым, но не является оптимальным, поскольку в
строке функции цели присутствует отрицательный коэффициент.
Выберем столбец, в котором функция цели имеет отрицательный коэффициент.
Для выбора строки с базисной переменной, которую необходимо сделать
небазисной, найдем симплексные отношения. Ведущий элемент выделен полужирный
шрифтом в таблице 3.2.
Пересчитаем таблицу в соответствии с правилами.
Таблица 3.3 - Вторая итерация
|
БП
|
Своб. чл.
|
НП
|
|
|
x1
|
x4
|
|
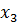
|
54
|
6
|
1
|
|
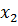
|
6
|
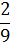
|
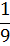
|
|
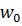
|
24
|
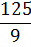
|
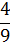
|
Решение является допустимым, так как нет отрицательных свободных членов.
Решение является оптимальным, так как нет отрицательных элементов в - строке.
Из симплекс-таблицы 3.3
получим:
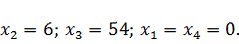
В
исходную функцию цели и ограничения входят только переменные 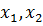
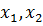 , поэтому
оптимальный план решения задачи:
, поэтому
оптимальный план решения задачи:
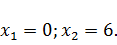
Найденное
решение 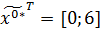
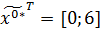 .
.
Тогда
координаты точки 
 можно
представить в виде:
можно
представить в виде:
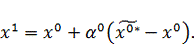
Подставим известные значения в выражение для определения координаты
следующей точки:
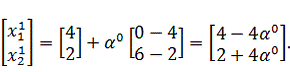
Найдем
величину шага 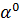
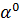 . Для
этого подставим в функцию (3.1) найденные выражения для
. Для
этого подставим в функцию (3.1) найденные выражения для 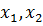
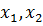 , т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум:
, т.е.
получим функцию зависящую от величины шага. Затем исследуем полученную функцию
на экстремум:
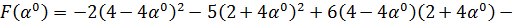
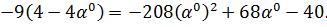
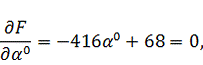
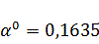
Найденное
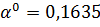
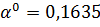 входит
интервал
входит
интервал 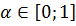
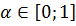 . Тогда
координаты следующей точки определятся по выражению:
. Тогда
координаты следующей точки определятся по выражению:
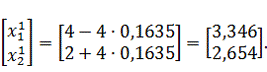
Шаг 2.
Найдем
направление вектора градиента по выражению (3.2) в точке 
 :
:
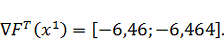
Составим
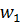
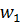 для
текущего шага:
для
текущего шага:
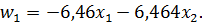
Решим задачу
линейного программирования:
Для получения решения данной задачи составим симплекс-таблицу и решим ее
согласно правилам:
Таблица 3.4 - Исходная
симплекс-таблица
|
Шаг 1.
|
|
БП
|
Своб. чл.
|
НП
|
|
|
x1
|
x2
|
|
x3
|
0
|
4
|
-9
|
|
x4
|
54
|
2
|
9
|
|
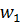
|
0
|
6.46
|
6.464
|
Решение является допустимым, так как нет отрицательных свободных членов.
Решение является оптимальным, так как нет отрицательных элементов в -строке.
Из симплекс-таблицы 3.4
получим:
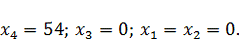
В
исходную функцию цели и ограничения входят только переменные 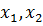
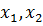 , поэтому
оптимальный план решения задачи:
, поэтому
оптимальный план решения задачи:
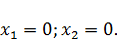
Найденное
решение 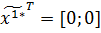
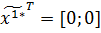 .
.
Тогда
координаты следующей точки можно представить в виде:
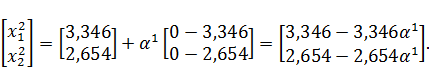
Найдем
величину шага 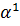
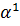 так же,
как и на предыдущем шаге:
так же,
как и на предыдущем шаге:
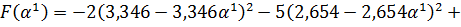
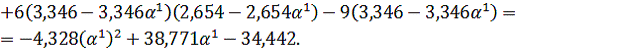
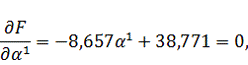
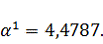
Найденное
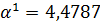
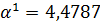 не
входит интервал
не
входит интервал 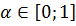
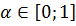 . Поэтому
в качестве
. Поэтому
в качестве 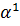
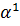 выберем
правую границу интервала
выберем
правую границу интервала 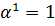
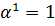 . Тогда
координаты следующей точки определятся по выражению:
. Тогда
координаты следующей точки определятся по выражению:
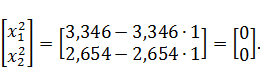
Найдем
направление вектора градиента по выражению (3.2) в точке 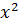
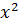 :
:
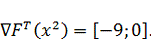
Вектор градиента направлен в вершине ОДЗП так, что не позволяет двигаться
ни внутрь ОДЗП, ни по ее границам.
Графическая интерпретация решения задачи методом линейных комбинаций
представлена на рисунке 3.5.
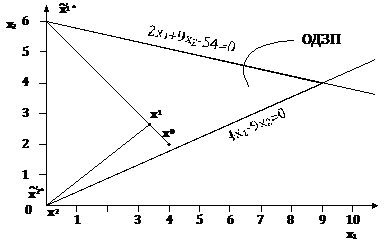
Рисунок
3.5 - Графическая интерпретация метода линейных комбинаций
Решение
методом линейных комбинаций совпадает с решением методом Зойтендейка и методом
Куна-Таккера.
фазочастотный симплекс экстремум функция
Заключение
В первой части курсового проекта выполнен анализ линейной системы 3-го
порядка, заданной в виде передаточной функции. Получены выражения для
построения временных характеристик системы. По заданной передаточной функции
были построены логарифмические амплитудно-частотная и фазочастотная
характеристики. Правильность результатов построения подтверждена моделированием
в пакете Matlab/Simulink.
Также на основании заданной передаточной функции были составлены
уравнения состояния в нормальной и канонической формах. Получены схемы моделей
системы и проведено моделирование в пакете Matlab/Simulink.
Во второй части курсового проекта решена прямая задача линейного
программирования с применением симплекс-таблиц, составлена и решена
двойственная задача к прямой. Решение прямой задачи и полученное решение при
приведении в соответствие переменных двойственной и прямой задачи совпадает.
Также решена частично-целочисленная задача.
В третьей части курсового проекта решены задачи нелинейного
программирования без ограничений и с ограничениями. В решении задачи без
ограничений показано, что методом Ньютона-Рафсона задача решается за один шаг,
а метод наискорейшего спуска медленно сходится к решению. В задаче нелинейного
программирования с ограничениями показано, что все методы решения задач
одинаково сходятся к одному решению, но за разное количество шагов. Приведены
графики интерпретации метода наискорейшего спуска, метода допустимых
направлений Зойтендейка и метода линейных комбинаций.
Список использованных источников
[1] Павлова А.В. Электронный учебно-методический комплекс
по учебной дисциплине «Математические основы теории систем» для студентов
специальности 1-53 01 07 Информационные технологии и управление в технических
системах [Электронный ресурс] / А.В. Павлова, М.К. Хаджинов. - Режим доступа: EUMK_MOTS_2013.zip.
[2] Павлова А.В. Математические основы теории систем:
конспект лекций для студентов специальности «Информационные технологии и
управление в технических системах». В 2 ч. / А.В. Павлова. - Минск: БГУИР,
2010. - Ч. 2. - 144 с.
[3] Певзнер Л.Д. Математические основы теории систем / Л.Д.
Певзнер, Е.П. Чураков - М. : Высш. шк., 2009.