Численные методы решения экстремальных задач
Реферат
Численные методы решения экстремальных задач
Введение
Численные методы решения - методы
вычислительной математики, применяемые для поиска экстремумов (максимумов или
минимумов) функций и функционалов. Для численного решения экстремальных задач,
рассматриваемых в бесконечномерных функциональных пространствах (задач
оптимального управления процессами, описываемыми обыкновенными
дифференциальными уравнениями или уравнениями с частными производными) могут
быть использованы после соответствующего обобщения многие методы
математического программирования, разработанные для задач минимизации или
максимизации функций конечного числа переменных. При этом в конкретных задачах
весьма важен правильный выбор подходящего функционального пространства, в
котором следует ее рассматривать. При выборе такого пространства обычно
учитываются физические соображения, свойства допустимых управлений, свойства
решений соответствующих задач при фиксированном управлении и т.п.
1. Оптимизация функции
одной переменной
Существует довольно очевидная
теорема: «Если непрерывная функция на концах некоторого интервала имеет
значения разных знаков, то внутри этого интервала у нее есть корень (как
минимум, один, но м.б. и несколько)». На базе этой теоремы построено численное
нахождение приближенного значения корня функции. Обобщенно этот метод
называется дихотомией, т.е. делением отрезка на две части. Обобщенный алгоритм
выглядит так:
1. Задать начальный интервал [a; b];
2. Убедиться, что на концах
функция имеет разный знак;
. Выбрать внутри интервала
точку X;
. Сравнить знак функции в
точке X со знаком функции в одном из концов;
. Если совпадает, то
переместить этот конец интервала в точку X;
. Иначе переместить в точку X
другой конец интервала, пока не будет достигнута нужная точность.
Варианты метода дихотомии
различаются выбором точки деления. Рассмотрим варианты дихотомии: метод
половинного деления и метод хорд.
. Метод половинного
деления
Метод половинного деления известен
также как метод бисекции. В данном методе интервал делится ровно пополам.
Такой подход обеспечивает
гарантированную сходимость метода независимо от сложности функции - и это
весьма важное свойство. Недостатком метода является то же самое - метод никогда
не сойдется быстрее, т.е. сходимость метода всегда равна сходимости в наихудшем
случае.
Метод половинного деления:
1. Один из простых способов
поиска корней функции одного аргумента.
2. Применяется для нахождения
значений действительно значной функции, определяемому по какому-либо критерию
(это может быть сравнение на минимум, максимум или конкретное число).
. Метод половинного
деления как метод поиска корней функции
Изложение метода: Перед применением
метода для поиска корней функции необходимо отделить корни одним из известных
способов, например, графическим методом. Отделение корней необходимо в случае,
если неизвестно на каком отрезке нужно искать корень.
Будем считать, что корень t функции f(x)=0 отделён на отрезке [a; b].
Задача заключается в том, чтобы найти и уточнить этот корень методом половинного
деления. Другими словами, требуется найти приближённое значение корня с
заданной точностью ɛ.
Пусть функция f непрерывна на
отрезке [a; b],
(a)*f(b)>0, ɛ=0,01 и t ϵ [a; b] - единственный корень уравнения.
Мы не рассматриваем случай, когда
корней на отрезке [a; b] несколько, то есть более одного. В качестве ϵ можно взять
и другое достаточно малое положительное число, например 0,001.
Поделим отрезок [a; b] пополам. Получим точку c=(a+b)/2, a<c<b и два отрезка [a; c], [c; b].
· Если f(c)=0,
то корень t найден (t=c).
· Если
нет, то из двух полученных отрезков [a; c], [c; b] надо выбрать один [a1; b1] такой,
что f(a1)*f(b)<0.
Новый отрезок [a1; b1] делим
пополам. Получаем середину этого отрезка c1=(a1+b1)/2 и так далее.
Для того, чтобы найти приближённое
значение корня с точностью до ɛ>0, необходимо остановить процесс
половинного деления на таком шаге n, на котором bn-cn<ɛ и вычислить x=(an+bn)/2. Тогда можно взять t~x.
4. Метод половинного
деления как метод оптимизации
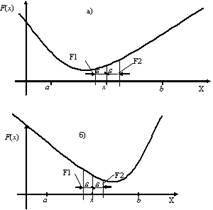
Рис. 1. Поиск экстремума функции F(x)
методом половинного деления
Рис. 2. Схема алгоритма метода
половинного деления
Однопараметрическая
оптимизация (поиск экстремумов
функций одной переменной) является самостоятельной и часто встречаемой задачей.
Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума
функции многих переменных.
Рассмотрим метод половинного деления
как простейший однопараметрический метод безусловной оптимизации. Данный метод
является методом прямого поиска. В нем при поиске экстремума целевой функции
используются только вычисленные значения целевой функции.
Дана функция F(x). Необходимо найти x,
доставляющий минимум (или максимум) функции F(x) на интервале [a; b] с заданной
точностью ɛ, т.е. найти x=argminF(x), x ϵ [a; b].
. Метод хорд
Недостаток деления отрезка строго
пополам проистекает от того, что он использует лишь знак функции, игнорируя
отклонение (абсолютную величину). Но очевидно, что чем меньше (по абсолютной
величине) значение функции, тем ближе мы находимся к корню. Метод хорд
предлагает делить отрезок в точке, отстоящей от краев отрезка пропорционально
абсолютному значению функции на краях. (Название «метод хорд» происходит от
того, что точка деления является пересечением отрезка [a; F(a), b; F(b)] -
хорды - с осью абсцисс.)
Изложение метода: Метод основан на
замене функции F(x) на каждом шаге поиска хордой, пересечение которой с осью X дает
приближение корня.
Рис. 3. Метод хорд
При этом в процессе поиска семейство
хорд может строиться:
1. при фиксированном левом
конце хорд, т.е. z=a, тогда начальная точка x0=b (рис. 3а);
2. при фиксированном правом
конце хорд, т.е. z=b, тогда начальная точка x0=a (рис. 3б);
В результате итерационный процесс
схождения к корню реализуется формулой:
· для
случая а):
· для
случая б):
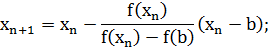
Процесс поиска продолжается до тех
пор, пока не выполнится условие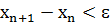 
.
Метод обеспечивает быструю
сходимость в том конце интервала [a; b], где знаки функции f(z) и ее кривизны f
совпадают.
. Комбинация метода хорд
и метода половинного деления
Метод хорд можно применить в
качестве «последнего штриха» после того, как метод половинного деления
гарантирует требуемую точность - это не улучшит существенно гарантируемой
точности, но, скорее всего, на несколько порядков повысит точность решения.
Если применять аналогичное уточнение
к интервалу, полученному методом хорд, то эффект будет значительно слабее. Это
ещё раз иллюстрирует тот факт, что метод хорд очень хорошо работает в условиях
малого интервала (близости обеих границ интервала к корню), но неспособен сам
создать себе эти условия (приблизить обе границы к корню).
На вопрос о том, стоит ли
использовать попеременное применение метода половинного деления и метода хорд,
ответ отрицателен. После того, как метод хорд приближает одну из границ почти
вплотную к корню, методу половинного деления придётся долго работать, чтобы
гарантировать заданную точность, т.к. метод хорд ее гарантировать не может.
Коэффициент K следует не задавать, а
вычислять по ходу работы: если при очередной операции интервал уменьшился более
чем в два раза (это то, что гарантирует метод половинного деления), то значит,
нужно больше доверять методу хорд (уменьшить K), и наоборот.
Может показаться, что при большом
доверии к методу хорд этот комбинированный метод работает так же, как метод
хорд. На самом деле, это не так: метод хорд передвигает по направлению к корню
только одну границу, а комбинированный метод даже при высоком доверии к методу
хорд передвигает и вторую границу, обеспечивая лучшие условия для работы метода
хорд, а значит - для ещё большего доверия к нему.
. Упрощенный метод
Ньютона
Эта модификация метода Ньютона
используется, если производная f /(x) представляет собой сложную
функцию, и для ее вычисления на каждой итерации используется много времени.
Зададим x0 - начальное приближение и вычислим производную z=f /(x0).
На следующих итерациях используется вычисленное значение производной: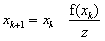 
. Это упрощение несколько замедляет процесс сходимости к решению,
однако сокращает время каждого итерационного цикла
Применение интерполяции для решения
уравнений:
В настоящем исследовании будут
рассмотрены методы решения уравнения f(x) = 0 с помощью применения
интерполяции. Мы выясним, есть ли преимущества при замене исходной функции на
интерполяционную функцию, и какова точность нахождения корня при переходе к
решению интерполяционного уравнения.
Постановка задачи: Пусть на отрезке
[a, b] задана функция f(x), и необходимо решить уравнение f(x) = 0 на этом
отрезке. Известно много различных способов нахождения корней уравнения, но мы
поступим следующим образом: будем приближать исходную функцию f(x) другой
функцией g(x) и искать корни именно интерполированной (в англоязычной
аббревиатуре - Interpolation) функции g(x).
Рассмотрим следующие методы
интерполяции:
· Интерполяция
каноническим полиномом
· Интерполяция
полиномами Лагранжа
· Интерполяция
степенными рядами
· Интерполяция
кубическими сплайнами
· Тригонометрическая
интерполяция
Сравним методы интерполяции функций
и выясним, какой из них лучше использовать для нахождения корней уравнения f(x)
= 0 в конкретном случае. В конечном итоге предстоит определить, насколько точно
корни уравнения g(x) = 0 приближают корни уравнения f(x) = 0.
. Интерполяция
каноническим полиномом
Рассмотрим в качестве функции f(x) =
sin(x) на [1,8], а в качестве интерполирующей функции g(x) - полином, имеющий
следующий вид:
В качестве узлов интерполяции
выберем точки на отрезке [1,8] по алгоритму Чебышева. При выборе 8 узлов
получается наименьшая ошибка интерполяции (она равна 0.0124).
График синуса (показан синим цветом)
и интерполирующей функции (показан красным цветом) в этом случае выглядит так:
Корни полинома g(x) = 0 будем
искать, например, методом Гаусса. Ошибка при нахождении поиске складывается из
ошибки интерполяции и ошибки решения уравнения.
Погрешность интерполяции: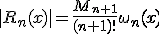 
Сложность метода Гаусса: O (2n/3).
10. Интерполяция
полиномами Лагранжа
Рассмотрим в качестве f(x) ту же
функцию sin(x), но на этот раз на отрезке [-3,3], а в качестве интерполирующей
функции g(x) рассмотрим полином:
где 
- полиномы степени n вида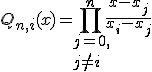 
В качестве узлов интерполяции снова
по алгоритму Чебышева выберем точки на отрезке [-3, 3].
График синуса (показан красным
цветом) и интерполирующей функции (показан зелёным цветом) в этом случае
выглядит так:
Уравнение Лагранжа g(x) = 0 решается
проще, чем f(x) = 0. При этом ошибка приближения: 0.0944, погрешность
интерполяции:
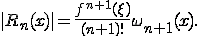
интерполяция численный переменная
Ошибка нахождения корней снова
складывается из ошибки интерполяции и ошибки решения уравнения Лагранжа.
. Интерполяция
степенными рядами
В качестве f(x) снова рассматриваем
sin(x) на [-1, 1], g(x) в данном случае имеет следующий вид:
Графики показаны на следующем
рисунке:
Ошибка приближения в этом случае
больше, поэтому данный метод интерполяции менее предпочтителен для поиска
корней, погрешность интерполяции:
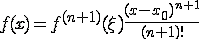
. Интерполяция
кубическими сплайнами
(x) = sin(x) на [-1, 1]. g(x) -
сплайн-интерполяция синуса, функцию f(x) пытаемся представить в виде некоторых
элементарных функций:
где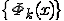 
- фиксированный линейно независимые функции, 
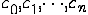- не определённые пока коэффициенты.
При выборе шага h = 0.25
интерполяция выглядит так:
Ошибка интерполяции оценивается как
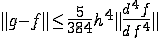
13. Тригонометрическая
интерполяция
На этот раз разложим функцию f(x)
(считаем её непрерывно-дифференцируемой) в ряд Фурье:
, где 
Для её приближения будем
использовать тригонометрический полином следующего вида:
Тогда приближение функции f(x)
функцией g(x) будет выглядеть примерно следующим образом:
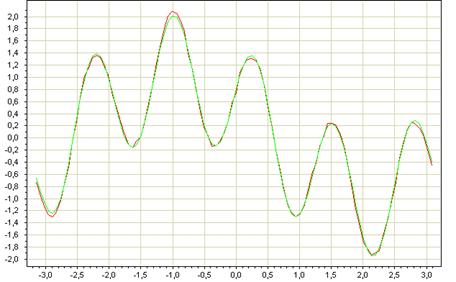
Поиск корней тригонометрической
функции осуществляется итерационным методом. Анализ данного метода будет дан
ниже.
14. Анализ методов
При решении уравнения f(x) = 0
вместо поиска корней исходной функции f(x) мы переходили к интерполирующей
функции g(x) и искали её корни. Но какой же метод аппроксимации лучше для
поиска корней?
Однозначного ответа на данный вопрос
быть не может - это зависит от функции f(x). С одной стороны, надо использовать
тот метод, который лучше приближает исходную функцию f(x). С другой стороны, мы
должны достаточно точно отыскать корни g(x).
Например, если сравнивать
интерполяцию каноническим полиномом и полиномами Лагранжа, то лучше
использовать второй метод, ибо он наиболее точно и с меньшими затратами
приближает требуемую функцию, а сложность решения уравнения g(x) = 0 у них
одинакова.
А интерполяцию кубическими сплайнами
рационально применять, если f(x) - периодическая или тригонометрическая
функция. В случае приближения сплайнами, например, кусочно-линейной функции
возникает следующий эффект:
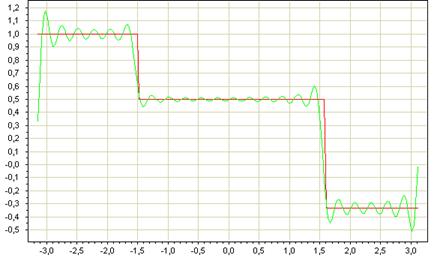
Понятно, что ни о какой точности
решения уравнения g(x) = 0 говорить не приходится.
15. Метод Коши
(наискорейшего спуска или крутого восхождения)
При использовании градиентного
метода в задачах оптимизации основной объем вычислении приходится обычно на вычисление
градиента целевой функции в каждой точке траектории спуска. Поэтому
целесообразно уменьшить количество таких точек без ущерба для самого решения.
Это достигается в методе Коши (наискорейшего спуска). Согласно этому методу,
после определения направления поиска оптимума в начальной точке, в этом
направлении делают не один шаг, а двигаются до тех пор пока происходит
улучшение функции, достигая таким образом, экстремума в некоторой точке. В этой
точке вновь определяют направление поиска (с помощью градиента) и ищут новую
точку оптимума целевой функции и т.д. (см. рис. 5.9). В этом методе поиск
происходит более крупными шагами, и градиент функции вычисляется в меньшем
числе точек (см. рис. 5.9). Заметим, что метод наискорейшего спуска сводит
многомерную задачу оптимизации к последовательности одномерных задач
оптимизации, которые могут решаться, например, методом золотого сечения или
половинного деления.
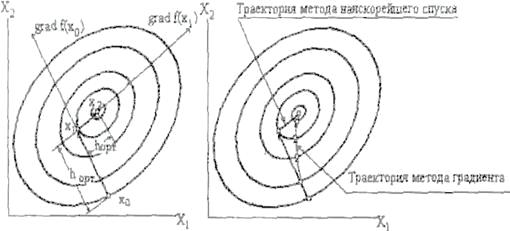
Метод наискорейшего спуска
а) Поиск максимума с выбором
оптимального шага.
б) Сравнение с методом градиента.
Величину шага h можно определить из
условия минимума f(Xk+hkSk):
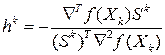
Вывод
Были рассмотрены следующие методы
интерполяции исходной функции для решения уравнения f(x) = 0:
· Интерполяция
каноническим полиномом
· Интерполяция
полиномами Лагранжа
· Интерполяция
степенными рядами
· Интерполяция
кубическими сплайнами
· Тригонометрическая
интерполяция
Установлено, что точность решения
интерполяционного уравнения зависит от вида функции f(x). В результате чего в
качестве рекомендации предлагается следующее:
· интерполировать
функцию f(x) различными способами,
· выбрать
метод, на котором достигается минимальная ошибка интерполяции,
· искать
корни этого метода.
Оптимизация функций нескольких
переменных
Список литературы
2. Горячев Л.В. Одномерная минимизация. Методические указания
к самостоятельной работе студенто
. по курсу «Методы оптимизации» - кафедра процессов
управления ДВГУ, 2003
. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные
методы. Изд-во «Лаборатория базовых знаний». Москва. 2003.
. И.С. Березин, Н.П. Жидков. Методы вычислений. Изд.
ФизМатЛит. Москва. 1962.
. А.А. Самарский, А.В. Гулин. Численные методы М.: Наука,
1989.
. А.А. Самарский. Введение в численные методы М.: Наука,
1982.
. Дж. Форсайт, М. Мальком, К. Моулер. Машинные методы
математических вычислений. Изд-во «Мир». Москва.