Размерность фрактальных поверхностей

Размерность фрактальных поверхностей

Контрольная работа

Размерность фрактальных поверхностей

Содержание

1. Введение в размерность

. Размерность геометрических объектов

. Природные фракталы

. Размерность Хаусдорфа-Безиковича

. Измерение длины негладкой (изломанной) линии

. Фрактальная размерность

. Подобие и скейлинг

. Самоподобие и самоаффинность

. Показатель Хёрста

. Соотношение "периметр-площадь"

. Размерность фрактальных поверхностей

Список литературы

. Введение в размерность

Важной характеристикой инженерной поверхности, наряду со стандартными параметрами шероховатости, является фрактальная размерность. Рассмотрим один из способов определения фрактальной размерности поверхности по соотношению "периметр-площадь".

Как известно, эвклидова размерность точки DE=d=0. Найдем размерность геометрических фигур, взяв в качестве примера диаметральное сечение шара радиусом r:

·        длина (диаметр) L=2r (L=Vd=1),

·        площадь сечения A=pr2 (A=Vd=2),

·        объем шара V=(4/3)pr3 (V=Vd=3).

Эти известные измеряемые величины могут быть определены по общей формуле

Здесь

где Г(х) − гамма функция, равная

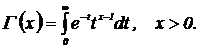
Если n − целое число, то

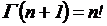 при n=0,1,2,…

. Размерность геометрических объектов

Размерность фрактального объекта определяется исходя из понятия фрактала. Фрактал - это множество, размерность Хаусдорфа-Безиковича которого строго больше топологической размерности. Фрактал обладает дробной размерностью.

В двухмерном случае фрактальную кривую получают с помощью некоторой ломаной линии (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную линию, заменяется на ломаную - генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал.

Рассмотрим один из таких фрактальных объектов - триадную кривую Коха. Построение кривой начинается с отрезка единичной длины (рис. 1) − это 0-е поколение кривой.

Рис. 1. Процедура построения кривой Коха

Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный через n=1. В результате такой замены получается следующее поколение кривой Коха. В 1-м поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/

Для получения 3-го поколения проделываются те же действия: каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом.

Кривая Коха представляет собой структуру, состоящую из частей, которые в некотором смысле подобны целому. Такие геометрические объекты относят к самоподобным объектам. Это означает, что в широком диапазоне масштабов топографические особенности и повторения объекта одни и те же.

Так, для кривой Коха, выбрав фрагмент, равный 1/3 отрезка линии, длиной, равной единице, и увеличив его в три раза, получим исходный отрезок, равный единице. Такие объекты обладают скейлингом, или масштабом измерения.

На рис. 1 представлены три поколения кривой. Если взять за основу не прямую, а треугольник и применить тот же алгоритм для каждой из сторон, то мы получим фрактал, называемый снежинкой (островом) Коха (рис. 2).

Рис. 2. Остров ("снежинка") Коха

При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев направления смещения середин отрезков должны чередоваться. На рис. 2 представлены первые поколения кривой, построенной по описанному принципу.

Предельная фрактальная кривая (при n→ ∞) называется "драконом" Хартера-Хейтуэя (рис. 3). На рис. 4 представлен "ковер" польского математика Серпинского.

Рис. 3. Процедура построения "дракона" " Хартера-Хейтуэя

Рис. 4. Построение "ковра" Серпинского

. Природные фракталы

Облака, горы, кусты, деревья и другие растения тоже имеют фрактальную структуру. Рассмотрим процесс роста куста (рис. 5). Сначала появилась веточка, потом она выпустила два побега, на следующем этапе каждый побег вновь раздвоился, то же самое происходит на следующем этапе, и в результате из начальной "вилки" двух побегов вырастает причудливое самоподобное растение.

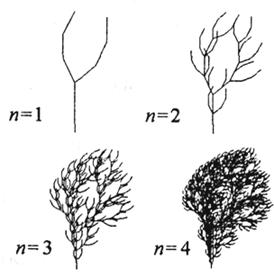
Рис. 5. Модель куста

Оно получено многократным повторением исходного эталона (n=1). На рис. 5 и 6 показаны примеры построения фрактальных объектов, сходных с природными образованиями (рис. 7).

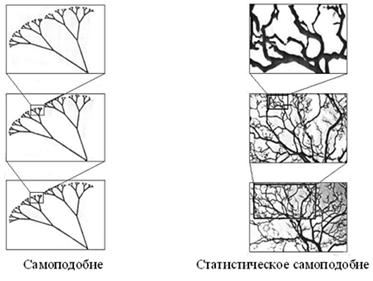
Рис. 6. Построение фрактального объекта

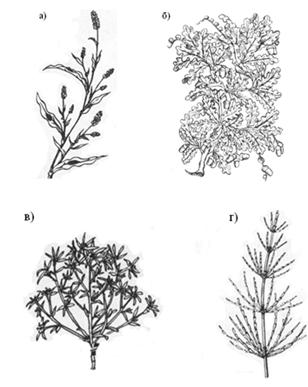
Рис. 7. Природные фрактальные объекты:

а - горец почечуйный; б − дуб; в − сушеница топяная; г - хвощ

. Размерность Хаусдорфа-Безиковича

Для оценки размерности Хаусдорфа-Безиковича рассмотрим измерение множества точек ℒ метрического пространства (рис. 8).

Рис. 8. Точки в метрическом Пространстве

Разобьем пространство на квадратные ячейки с размером стороны ячейки δ и подсчитаем число ячеек, покрывающих это множество. Уменьшение размера ячейки приводит к росту числа ячеек, покрывающих множество. Каждая ячейка имеет площадь δ2, тогда площадь множества

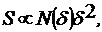
где N(δ) - число ячеек, покрывающих множество.

Рассмотрим некоторые величины, характеризующие множество. Так, "длина" поверхности определяется выражением

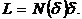
Так как 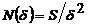, то "длина" поверхности, определяемая предельным переходом, равна:

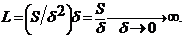
"Объем" поверхности

Таким образом, "длина" множества стремится к бесконечности, а "объем" − к нулю.

Для характеристик" величины" (длины, объема) множества точек ℒ используется некоторая пробная функция 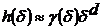, которая определяет размеры ячейки: длину при d=1, площадь при d=2, объем при d= "Величина", или мера множества ℒ определяется как сумма "величин" всех ячеек, покрывающих метрическое пространство ℒ:

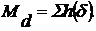
Константа  зависит от формы ячеек (для квадратной ячейки ).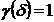

При некотором показателе степени d мера Md при δ→0 равна либо нулю, либо бесконечности, либо некоторому (не обязательно целому) конечному положительному числу. Значение d, при котором мера Md не равна нулю или бесконечности, адекватно отражает топологическую размерность множества ℒ.

Число dcr такое, что

называется размерностью Хаусдорфа-Безиковича.

Для "простых" (не фрактальных) геометрических объектов размерность Хаусдорфа-Безиковича совпадает с топологической размерностью. Для фрактальных объектов скачок меры Md от нуля к бесконечности происходит при дробных значениях d.

Пусть функция N(δ) зависит от δ со степенной особенностью в нуле

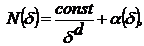
где α(δ)δd →0 при δ→0.

С точностью до бесконечно малых величин запишем

Откуда

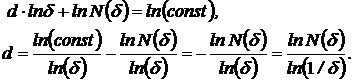
Таким образом, имеем

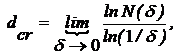
. Измерение длины негладкой (изломанной) линии

Как измерить длину береговой линии?

Рассмотрим следующие сравнительно простые приемы измерения.

Пометим точками A и B начало и конец измеряемого участка (рис. 9).

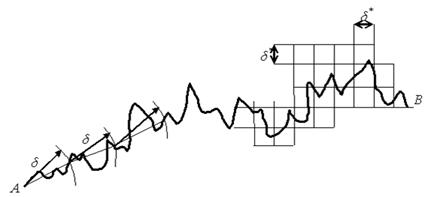
Рис. 9. Измерение длины линии раствором циркуля или с помощью сетки

Одна из процедур измерения длины заключается в следующем.

Будем измерять длину линии от точки А до точки B отрезками длиной δ.

Подсчитав число отрезков, найдем длину 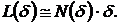 С уменьшением раствора циркуля δ число отрезков N(δ) растет. Типичная зависимость L(δ) от δ в логарифмических координатах представлена на рис. 10.

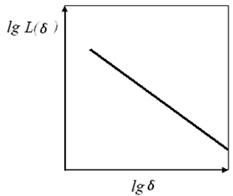
Рис. 10. Зависимость измеренной длины изломанной (береговой) линии от масштаба (длины отрезка δ)

Не останавливаясь на недостатках этого метода, особенно при определении фрактальной размерности профиля шероховатой поверхности, рассмотрим другой (альтернативный) метод.

Покроем рассматриваемый участок квадратной сеткой (правая часть рис. 9) и подсчитаем число ячеек, покрывающих рассматриваемую линию.

Уменьшение размера ячеек приводит к увеличению числа ячеек, покрывающих линию AB. Следует ожидать, что число шагов измерительного циркуля или число покрывающих линию ячеек будет обратно пропорционально δ или δ*х δ*, а величина  будет стремиться к постоянному для данной линии значению L(δ). Однако при уменьшении δ или размера ячеек сетки длина линии не стремится к постоянному значению. При δ→0 измеряемая длина непрерывно растет, т.е. при δ→0 величина L(δ) не является пределом.

Измеренная длина линии может быть описана следующей приближенной формулой:

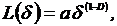
где D - фрактальная размерность линии.

Легко показать, что для прямой линии и, например, для окружности D=1. Длина окружности при уменьшении δ стремится к постоянному значению, равному 2πR, где R-радиус окружности.

фрактальный размерность поверхность скейлинг

6. Фрактальная размерность

Б. Мандельброт (B.B. Mandelbrot) предложил следующее определение фрактала. Фракталом называется множество, размерность Хаусдорфа-Безиковича (Х-Б) которого строго больше его топологической размерности (Е. Федер, 1991). Нестрогое определение, не требующее разъяснения понятий множество, размерность Х-Б, топологическая размерность, формулируется так: фрактал − это структура, состоящая из частей, подобных целому. Или еще проще: фрактал - это структура с дробной размерностью.

Зависимость N(δ) числа отрезков δ (или числа ячеек, покрывающих линию) от размера отрезка (или размера ячеек) описывается следующим с точностью до множителя 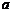 соотношением:

где D - фрактальная размерность.

Если построить зависимость lgN(δ)-lg(δ), то фрактальная размерность равна угловому коэффициенту (наклону) графика, т.е.

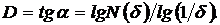
Размерность, определяемая путем подсчета числа клеток (ячеек), покрывающих линию в зависимости от размера клетки, называют клеточной размерностью.

Фрактальная размерность поверхности. Покроем исследуемый участок поверхности системой одинаковых треугольников и подсчитаем суммарную площадь покрытия, равную

,

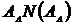где AΔ-площадь треугольника. Разделим полученную площадь на величину номинальной площади-проекции реальной поверхности на плоскость, определяемую геометрическим очертанием исследуемого участка.

Тогда, построив в двойных логарифмических координатах зависимость относительной площади покрытия от площади покрывающего элемента, можно найти в определенном диапазоне изменения площади элемента наклон или угловой коэффициент прямой, величина которого берется со знаком минус.

В результате расчета находят фрактальную размерность поверхности, равную

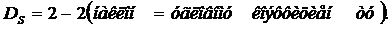
Фрактальная размерность поверхности изменяется в пределах 2<DS<3, а ее связь с фрактальной размерностью профиля определяется соотношением DS=D+1.

. Подобие и скейлинг

Дадим определение геометрического подобия.

Две геометрические фигуры называются подобными, если: 1) угол между каждыми двумя линиями в одной из них равен углу между соответствующими линиями в другой и 2) каждый прямолинейный отрезок в одной из них находится в постоянном отношении с соответствующим ему отрезком в другой.

Так, два многоугольника подобны, если их соответствующие углы равны, а длины сторон, заключающих эти углы, пропорциональны.

Кроме геометрического подобия, различают кинематическое и динамическое подобия для механических явлений, лежащие в основе процедур моделирования.

Прямая линия при параллельном переносе остается самой собой.

Можно утверждать, что прямая инвариантна относительно параллельного переноса и изменения масштаба (скейлинга), т.е. она самоподобна.

Таким образом, скейлинг - это отражение масштабной инвариантности.

Для отрезка прямой единичной длины можно выбрать коэффициент подобия

(N)=1/N,

где N - любое целое число (N >1).

Прямоугольный участок плоскости можно покрыть уменьшенными копиями, если их длины изменить в r(N)=(1/N)1/2 раз.

Аналогично прямоугольный параллелепипед можно покрыть его уменьшенными копиями, выбрав масштабный множитель r(N)=(1/N)1/ В общем случае масштабный множитель следует выбрать равным

(N)=(1/N)1/d,

где d - размерность подобия, равная 1 - для прямой, 2 - для плоскости и 3 - для объемных фигур.

Для фрактальных геометрических структур размерность подобия Dp определяется выражением

. Самоподобие и самоаффинность

Для самоаффинного профиля можно записать

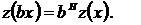
Здесь b-масштаб увеличения; Н-показатель степени (показатель Хёрста).

Показатель Хёрста изменяется в диапазоне 0<H<1. Для самоаффинных кривых связь между фрактальной размерностью и показателем Хёрста имеет вид D=2−H. Приведенное соотношение справедливо для профилограмм, запись которых ведется с разными масштабами увеличения в горизонтальном и вертикальном направлениях. Для случайного гауссовского процесса Н=0,5.

. Показатель Хёрста

Показатель Хёрста позволяет определить фрактальную размерность последовательности измерений, в частности, он использовался в качестве инструмента для статистической оценки высот волн [Е. Федер]. Считается установленной связь между показателем Хёрста и фрактальными размерностями высот волн и поверхности, которая выражается следующими простыми соотношениями для профиля и поверхности: D=2-H; DS=3-H. Рассмотрим методику определения показателя Хёрста.

. Находим N высот вершин выступов H={h1, h2,…,hN}T и определяем относительные значения этих высот х1,х2,…,хN, хiÎ[0,1], где 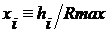. Если высоты выступов подчиняются бета-распределению, то значения хiº хib.

. Находим выборочное (из N высот выступов) среднее

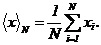
Определяем накопившееся отклонение

График изменения накопившегося отклонения для высот выступов, имеющих бета-распределение при N=50, представлен на рис. 11.

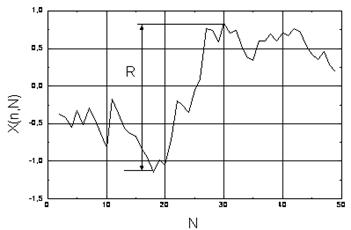
Рис. 11. Зависимость накопившегося отклонения X(n,N) от N

Из графика находим размах R.

. Вычисляем стандартное отклонение − выборочное среднее квадратическое отклонение относительных высот выступов

.

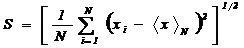. Представим отношение R/S, зависящее от показателя Хёрста, в виде

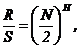
где Н-показатель Хёрста.

При репрезентативной выборке высот выступов показатель Н можно найти, используя приведенное эмпирическое выражение Хёрста. Представляет интерес найти зависимость R/S от числа рассматриваемых выступов N. Эта зависимость в логарифмических координатах будет представлять собой прямую линию, наклон которой определяется показателем Хёрста. Фрактальная размерность последовательности относительных значений высот выступов будет равна D=2-H.

Рассмотрим следующий пример. В качестве исходных данных были взяты ординаты профиля поверхности (с шагом 10 мкм). Длина трассы составила 800 мкм. Ординаты имели вертикальное увеличение, равное 50 000. На рис. 12 показаны профиль поверхности (кривая 1) и накопленное отклонение ординат от средней линии (кривая 2).

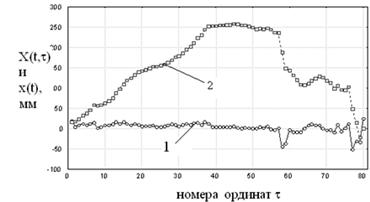
Рис. 12. Профиль поверхности (1) и накопленное отклонение (2) ординат от средней линии профиля

Размах зависит от рассматриваемой длины профилограммы (числа номеров ординат). Ясно, что размах растет с увеличением t. Зависимость нормального размаха, определяемого выражением (R/S), от t показана в логарифмических координатах для рассматриваемой стальной поверхности на рис. 1.

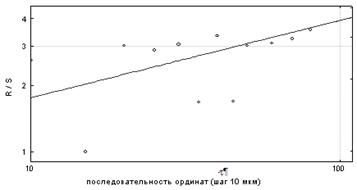
Рис. 13 Метод нормированного размаха для оценки фрактальной размерности профиля

Рассмотрим алгоритм определения показателя Хёрста с помощью метода наименьших квадратов (МНК). Будем искать уравнение регрессии в виде

=b+mx,

где y=lg(R/S), b=lg(a), m=H, x=lg(τ/2).

Вход: N (число точек), (ξi, ηi), i=1,2,…,N (координаты точек)

Выход: b=lg(a) (сдвиг), m=H (наклон)

Алгоритм:

=N=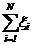==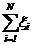==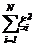=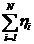A11A22−A21A12=d1A22−d2A12=A11d2−A21d1=lg(a)=D1/D

m=H=D2/D

Аппроксимирующей функцией зависимости, представленной на рис. 13, является степенная зависимость вида:

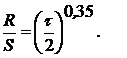
Таким образом, показатель Хёрста равен H=0,35, и фрактальная размерность профиля оценивается величиной D=2 - H=2 - 0,35=1,65.

Статистическая самоаффинность обусловлена сходством внешнего вида профиля при разных масштабах. Иными словами, шероховатая поверхность всегда негладкая при рассмотрении с разным увеличением.

При 0,5<H<1 - последовательность ординат профиля характеризуется эффектом долговременной памяти. При приближении показателя Хёрста к единице профиль становится гладким и не фрактальным.

При 0<H<0,5 - последовательность ординат профиля характеризуется отсутствием эффекта памяти.

В качестве примера на рис. 14 показана последовательность временного ряда (или ординат профиля шероховатой поверхности) и зависимость нормированного размаха от времени (длины профиля).

Рис. 14. Последовательность ординат и зависимость нормированного размаха от длины

Обращает на себя внимание разное значение показателя Хёрста на трех участках R/S - анализа. При малом числе элементов показатель Хёрста близок к единице и не совсем отражает фрактальную структуру объекта.

Сейлс и Томас (R.S. Sayles, T.R. Thomas) измерили и проанализировали шероховатость поверхностей разнообразных объектов, в том числе и инженерных металлических поверхностей.

Высота поверхности z измерялась в различных точках х вдоль некоторого направления. Имея большое число измерений по всему участку поверхности, можно рассчитать шероховатость поверхности, определяемую дисперсией:

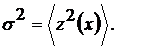
Здесь угловые скобки обозначают усреднение по серии измерений (иногда многократных повторных) топографии поверхности. Точка отсчета по вертикали выбирается так, что

Важной мерой статистических свойств поверхности является корреляционная функция, определяемая соотношением:

Для стационарных поверхностей корреляционную функцию можно выразить через спектр мощности G(w) с помощью преобразования Фурье

.

Здесь ω - частота.

Для шероховатой поверхности нижний и верхний пределы интегрирования будут соответствовать ω min и ω max.

Оценка частот характеризуется первым и вторым кроссоверами (рис. 1.3).

Для самоаффинного или самоподобного профиля поверхности спектральная плотность имеет степенной вид

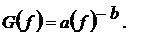
Здесь f - частота дискретизации; а и b - коэффициенты регрессии.

Коэффициент а носит название коэффициент изрезанности, а b - характеризует фрактальную размерность профиля.

. Соотношение "периметр-площадь"

Сравним соотношение "периметр-площадь" для нефрактальных (табл. 1) и фрактальных геометрических объектов.

1.      Нефрактальные объекты.

Таблица 1. Соотношение "периметр - площадь" в эвклидовой геометрии

2.      Фрактальные объекты.

По аналогии с нефрактальными объектами запишем соотношение "периметр-площадь" в виде

. (1)

Здесь P - периметр; A - площадь; R(δ) - параметр, зависящий от масштаба измерения (размера квадратной ячейки); D - фрактальная размерность "береговой" линии (1 < D < 2).

Учитывая, что периметр определяется выражением

,

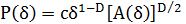запишем соотношение (1) в виде

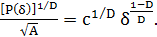. (2)

Здесь с - коэффициент.

Изменение периметра при разных масштабах измерения определяется по формуле

.

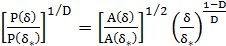Соотношение (2) выражает условие самоподобия "островов" с фрактальными границами (при этом масштаб измерения δ должен быть достаточно маленьким, чтобы точно измерять область наименьшего острова).

Прологарифмируем соотношение (2)

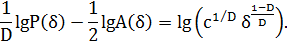
Преобразовав полученное выражение, запишем:

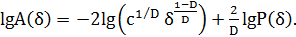 (3)

На рис. 15 показана зависимость "периметр - площадь", представленная в логарифмических координатах.

Угловой коэффициент прямой, представленной на рис. 15, равен 2/D.

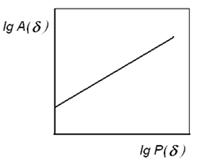
Рис. 3.15. Зависимость "площадь - периметр"

Анализ выражения (3) показывает, что величиной

-2lg(c1/Dδ1-D)/D),

зависящей от масштаба измерения δ, можно пренебречь, так как при достаточно большом масштабе измерения "остров" становится нефрактальным объектом. Действительно, при D=DE=1 и масштабе, при котором с=1, имеем:

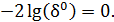
Окончательно запишем

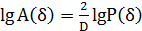. (4)

Из выражения (4) найдем фрактальную размерность "береговой" линии

График (рис. 15), построенный в двойных логарифмических координатах, отражает условие самоподобия и позволяет найти фрактальную размерность.

Процедура определения фрактальной размерности заключается в покрытии фрактального объекта − "острова" - квадратной сеткой с размером ячейки δ.

В этом случае периметр и площадь фигуры можно определить по формулам

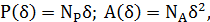 (5)

где 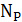 - число заполненных "береговой" линией ячеек;  - число ячеек, покрывающих площадь "острова".

Таким образом, после подсчета 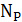 и , по формулам (5) и (4) вычисляется фрактальная размерность D.

Для определения фрактальной размерности поверхности используем подход, предложенный Б. Мандельбротом

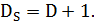
11. Размерность фрактальных поверхностей

Соотношение периметр-площадь используют, чтобы характеризовать множество фрактальных объектов, используемых в широком диапазоне научных и технических проблем.

В частности, это соотношение эффективно используется в работах, в которых дается характеристика поверхностей излома стали и методика для определения конкретных поверхностей изломов.

Применительно к инженерным поверхностям подобное соотношение используется редко. В основном при определении фрактальной размерности поверхности применяют метод покрытия. На рис. 16 представлены модели фрактальных поверхностей при разных значениях фрактальной размерности.

Для определения фрактальной размерности поверхности рассмотрим контакт фрактальной поверхности с гладкой.

В качестве примера возьмем сечение поверхности плоскостью, параллельной срединной плоскости. На рис. 17 представлено такое сечение фрактальной поверхности с DS = 2,6.

Рис. 16. Модели фрактальных поверхностей

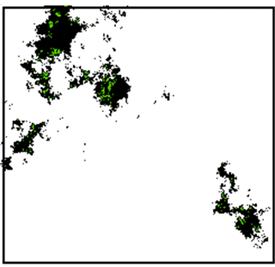
Рис. 17. Сечение фрактальной поверхности

Считается, что все "острова" на рис. 17 самоподобны. Тогда для анализа соотношения периметр-площадь выделим характерный "остров" (рис. 18).

Рис. 18. Изображение "острова"

На рис. 19 представлена процедура определения фрактальной размерности клеточным методом.

Рис. 19. К оценке фрактальной размерности: покрытие фрактального объекта сеткой с квадратными ячейками (Paul S. Addison)

На рис. 20 представлен график зависимости "площадь-периметр" в двойных логарифмических координатах, построенный на основании рис. 19.

При этом считаем, что число квадратов пропорционально соответствующим параметрам: площади и периметра

Зависимость числа клеток, покрывающих площадь "острова" NA, от числа клеток, в которых попала "береговая" линия острова NP , построенная в логарифмических координатах при разных размерах стороны квадратной ячейки, оценивается в данном примере уравнением регрессии

=-69,14+3,303NP.

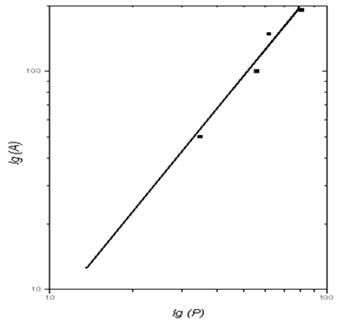
Рис. 20. Зависимости "площадь-периметр"

Фрактальная размерность определяется выражением

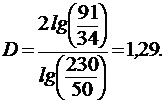
При исследовании контакта двух фрактальных поверхностей, имеющих свои фрактальные размерности, привлекательным моментом является замена двух фрактальных поверхностей на контакт гладкой поверхности с приведенной фрактальной.

С этой целью используем ранее рассмотренную процедуру. Смоделируем контакт двух поверхностей и определим пятна касания при некотором сближении.

На рис. 21 показана картина контакта двух поверхностей с выделенным для исследования "островом".

Рис. 21. Контакт фрактальных поверхностей

Список литературы

1.      Мандельброт Б. Фрактальная геометрия природы / Б. Мандельброт: [пер. с англ.]. - М.: Институт компьютерных исследований, 2012. - 656 с.

3.      Mandelbrot B.B. Fractal character of fracture surfaces of metals / B.B. Mandelbrot [et al.]//Nature, 1984. - V. 308. - P. 721-722.

.        Mu Z.Q. Studies on the fractal dimension and fracture toughness of steel / Z.Q. Mu, C.W. Lung // J. Phys. D: Appl. Phys., 1988. - V. 21. - P. 848-850.

5.      Sayles R.S. Surface topography as a nonstationary random process / R.S. Sayles, T.R. Thomas // Nature, 1978. - V. 271. - P. 431-434.

.        Addison P.S. Fractals and Chaos-An Illustrated Course / P.S. Addison. - Inst.of Physics Publishing. - Bristol, 2007.