Аналіз двоїстості та ортогоналізації функції
Вступ
Багато прогнозувальних задач стаціонарних
випадкових процесів (див. [2], [7], [10], [14]) еквівалентні пошуку відстані
від сталої функції 1 до підпростору 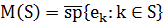 в
в 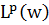 , де S - підмножина цілих чисел
, де S - підмножина цілих чисел 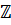 , ek = e-ikλ, w-невід’ємна
інтегрована функція на одиничному крузі T,
, ek = e-ikλ, w-невід’ємна
інтегрована функція на одиничному крузі T, 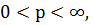 і
і 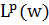 це зважений
це зважений 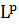 простір на T з нормою
простір на T з нормою 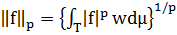 . Тут µ - це Лебегова
міра на Т, причому µ(T) = 1. Записуємо
. Тут µ - це Лебегова
міра на Т, причому µ(T) = 1. Записуємо

для відстані. Наприклад, 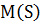 складається із
многочленів
складається із
многочленів 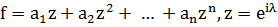 , і їх границь в
, і їх границь в 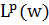 коли індексна множина S,
є пів пряма
коли індексна множина S,
є пів пряма 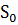 , тобто
, тобто
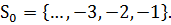
У цьому випадку, загальновідома теорема  стверджує, що для
стверджує, що для 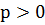 ,
,
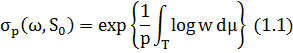
якщо 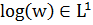 ; в іншому випадку
; в іншому випадку 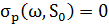 (див., наприклад, [5, p.
156]). У праці [10] для індексної множини
(див., наприклад, [5, p.
156]). У праці [10] для індексної множини 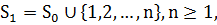 привернула значну увагу
до обчислення
привернула значну увагу
до обчислення 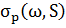 коли індексна множина
коли індексна множина 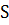 є
є 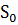 з обмеженою кількістю
доданих та видалених точок
з обмеженою кількістю
доданих та видалених точок 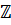 . На сьогодні, найбільш відомий загальний
результат - це Теорема 2 Ченга та ін., яка стверджує, що, для такого
. На сьогодні, найбільш відомий загальний
результат - це Теорема 2 Ченга та ін., яка стверджує, що, для такого 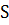 ,
, 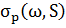 є позитивним лише за
умови що
є позитивним лише за
умови що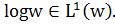 Однак, задача обчислення
Однак, задача обчислення
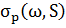 та функції
та функції 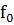 в
в 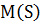 , що його досягає,
залишається недосяжною, навіть якщо
, що його досягає,
залишається недосяжною, навіть якщо 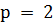 , за винятком кількох
особливих випадків, розглянутих у пункті 2. У цій роботі ми розв’язуємо задачу
пошуку обґрунтованої загальної індексної множини S, що могла б пролити світло
на труднощі, звичайні для цієї сфери досліджень. Пункт 3 представляє результати
для
, за винятком кількох
особливих випадків, розглянутих у пункті 2. У цій роботі ми розв’язуємо задачу
пошуку обґрунтованої загальної індексної множини S, що могла б пролити світло
на труднощі, звичайні для цієї сфери досліджень. Пункт 3 представляє результати
для 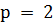 і містить деякі відкриті
питання щодо загального
і містить деякі відкриті
питання щодо загального 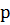 .
.
1. Теоретичні відомості
.1 Стаціонарні послідовності
Нехай 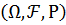 - ймовірнісний простір і
- ймовірнісний простір і
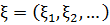 - деяка послідовність
випадкових величин. Позначимо через
- деяка послідовність
випадкових величин. Позначимо через 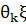 послідовність
послідовність 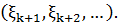
Означення 1
Випадкова послідовність 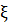 називається стаціонарною
(у вузькому сенсі), якщо для любого
називається стаціонарною
(у вузькому сенсі), якщо для любого 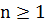 розподіли ймовірностей
розподіли ймовірностей 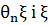 співпадають:
співпадають:
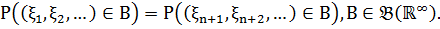
Означення 2
Послідовність комплексних випадкових величин 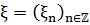 з
з 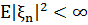 ,
, 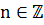 , називається
стаціонарною (в широкому сенсі), якщо для всіх
, називається
стаціонарною (в широкому сенсі), якщо для всіх 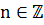
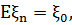
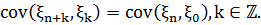
Позначимо
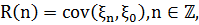
І припускаючи, що 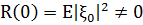
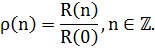
Функцію 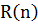 будемо називати
коваріаційною функцією, а
будемо називати
коваріаційною функцією, а 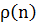 - кореляційною функцією стаціонарної (в широкому
сенсі) випадкової послідовності
- кореляційною функцією стаціонарної (в широкому
сенсі) випадкової послідовності 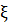 .
.
.2 Спектральний розклад кореляційної функції
Нехай
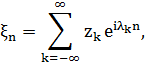
де 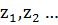 - ортогональні
- ортогональні 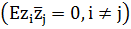 випадкові величини з
нульовими середніми і
випадкові величини з
нульовими середніми і 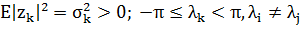 . Якщо покласти, що
. Якщо покласти, що 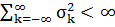 , то ряд
, то ряд 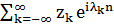 сходиться в
середньоквадратичному сенсі і
сходиться в
середньоквадратичному сенсі і
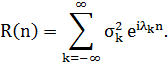
Введемо функцію
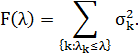
Тоді коваріаційна функція 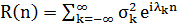 може бути записана у
вигляді інтеграла Лебега-Стілт’єса
може бути записана у
вигляді інтеграла Лебега-Стілт’єса
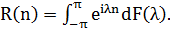
Теорема (Герглотц)
Нехай 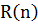 - коваріаційна функція
стаціонарної (в широкому сенсі) випадкової послідовності з нульовим середнім.
Тоді на
- коваріаційна функція
стаціонарної (в широкому сенсі) випадкової послідовності з нульовим середнім.
Тоді на 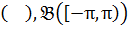 знайдеться така скінченна
міра
знайдеться така скінченна
міра 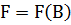 ,
,
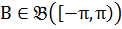 , що для любого
, що для любого 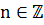
кореляційний екстраполяція ортогоналізація спектральний
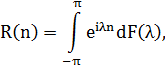
де інтеграл 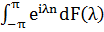 розуміється як інтеграл
Лебега-Стілт’єса по множині
розуміється як інтеграл
Лебега-Стілт’єса по множині 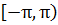 .
.
.3 Спектральне представлення стаціонарних (в широкому сенсі)
послідовностей
Теорема 1
Існує така ортогональні стохастична міра 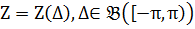 , що для кожного
, що для кожного 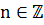 (
(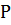 -м.н.)
-м.н.)
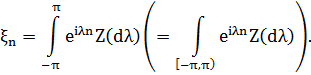
При цьому 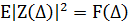 .
.
Теорема 2
Якщо 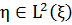 , то знайдеться така
функція
, то знайдеться така
функція 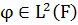 , що (
, що (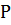 -м.н.)
-м.н.)
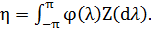
1.4 Регулярні
послідовності
Введемо позначення. Нехай 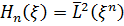 та
та 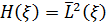 - замкнені лінійні
многовиди, породжені величинами
- замкнені лінійні
многовиди, породжені величинами 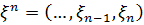 і
і 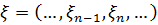 відповідно. Нехай також
відповідно. Нехай також
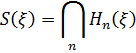
Означення
Стаціонарна послідовність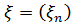 називається регулярною,
якщо
називається регулярною,
якщо
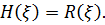
і сингулярною, якщо
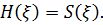
Теорема
Кожна стаціонарна в широкому сенсі випадкова
послідовність 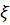 допускає єдиний розклад
допускає єдиний розклад
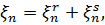
де 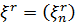 - регулярна, а
- регулярна, а 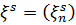 - сингулярна
послідовності. При цьому
- сингулярна
послідовності. При цьому 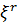 і
і 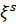 ортогональні (
ортогональні (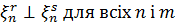 .
.
Означення
Клас Харді 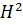 - це клас аналітичних
функцій
- це клас аналітичних
функцій 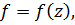 у відкритому одиничному
колі
у відкритому одиничному
колі 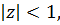 на комплексній площин,
які задовольняють умову
на комплексній площин,
які задовольняють умову
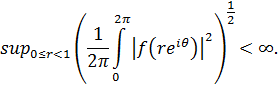
Теорема (Колмагоров)
Нехай 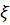 - не вироджена регулярна
стаціонарна послідовність. Тоді існує спектральна щільність
- не вироджена регулярна
стаціонарна послідовність. Тоді існує спектральна щільність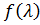 така, що
така, що
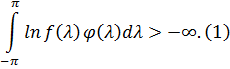
А саме, 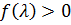 (майже скрізь по мірі
Лебега).
(майже скрізь по мірі
Лебега).
І навпаки, якщо 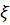 - деяка стаціонарна
послідовність, що має спектральну щільність, яка задовольняє умову (1), то ця
послідовність є регулярною.
- деяка стаціонарна
послідовність, що має спектральну щільність, яка задовольняє умову (1), то ця
послідовність є регулярною.
.5 Екстраполяція, інтерполяція та фільтрація
Екстраполяція
Розглянемо частковий випадок, коли спектральна
щільність задається у вигляді
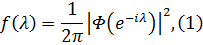
де функція 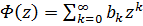 має радіус збіжності
має радіус збіжності 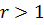 і не має нулів в радіусі
і не має нулів в радіусі 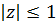
Нехай
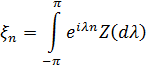
- спектральне представлення послідовності 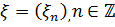 .
.
Теорема 1. Якщо спектральна
щільність послідовності 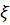 може бути представлена у вигляді (1), то
оптимальна (лінійна) оцінка
може бути представлена у вигляді (1), то
оптимальна (лінійна) оцінка 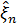 величини
величини 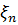 по
по 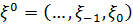 задається формулою
задається формулою
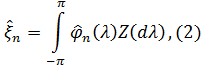
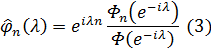
Інтерполяція
Найпростішою задачею інтерполяції є задача
побудови оптимальної (в середньоквадратичному сенсі) лінійної оцінки по
результатам спостережень 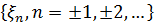 «пропущеного» значення
«пропущеного» значення 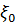 .
.
Позначимо через 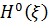 - замкнений лінійний
многовид, породжений величинами
- замкнений лінійний
многовид, породжений величинами 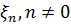 . Тоді кожна випадкова величина
. Тоді кожна випадкова величина 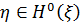 може бути представлена у
вигляді
може бути представлена у
вигляді
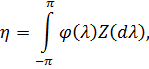
де 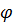 належить
належить 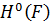 замкненому лінійному
многовиду, породженому функціями
замкненому лінійному
многовиду, породженому функціями 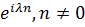 і оцінка
і оцінка
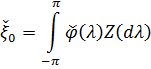
буде оптимальною тоді і тільки тоді, коли
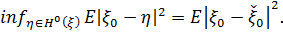
Із властивостей «перпендикулярів» в гільбертовому
просторі 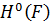 випливає, що функція
випливає, що функція 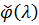 повністю визначається
двома умовами:
повністю визначається
двома умовами:
1) 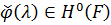
2) 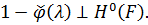
Теорема 2 (Колмагоров)
Нехай 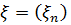 - регулярна
послідовність з
- регулярна
послідовність з
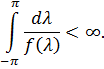
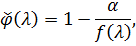
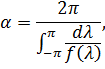
І похибка інтерполяції 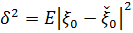 задається формулою
задається формулою 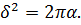
Фільтрація.
Задача фільтрації полягає в побудові оптимальної
(в середньоквадратичному сенсі) лінійної оцінки 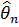 величини
величини 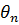 по тім чи іншим
спостереженням послідовності
по тім чи іншим
спостереженням послідовності 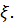
Оскільки 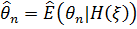 , то знайдеться така
функція
, то знайдеться така
функція 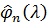 , що
, що
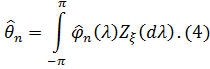
Оптимальна функція 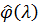 :
:
1) 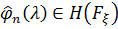 ,
,
2) 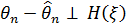 .
.
Отриманий розв’язок (4) можна використати для
побудови оптимальної оцінки 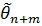 величини
величини 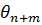 по результатам
спостережень
по результатам
спостережень 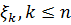 , де
, де 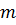 - деяке задане число з
- деяке задане число з 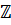 .
.
.6 Двоїстість та
ортогоналізація
Надалі ми припускаємо, що 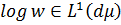 такий, що
такий, що 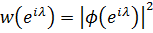 для деякої функції 𝜑 з класу Харді
для деякої функції 𝜑 з класу Харді 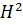 . Нехай
. Нехай 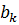 і
і 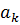 це коефіцієнти в
наступних розкладах:
це коефіцієнти в
наступних розкладах:
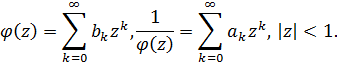
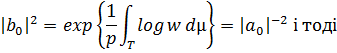
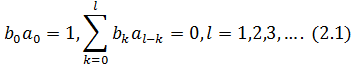
Явний вигляд для 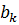 і
і 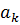 в термінах коефіцієнтів
ряду Фур’є для
в термінах коефіцієнтів
ряду Фур’є для 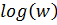 можна знайти в [11] та [12].
можна знайти в [11] та [12].
Для набору індексів 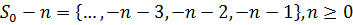 , котрі відповідають
видаленню перших n частот з
, котрі відповідають
видаленню перших n частот з 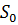 , відомо, що
, відомо, що
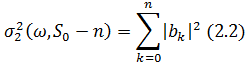
(див. [7], [11], [2]). Це так званий 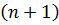 - й крок прогнозу
дисперсії. Для множини індексів
- й крок прогнозу
дисперсії. Для множини індексів 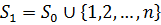 котрий дорівнює приєднанню наступних
котрий дорівнює приєднанню наступних 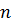 частот до
частот до 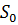 в [10] показано, що
в [10] показано, що
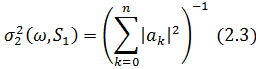
якщо 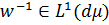 . Дуже цікавий обернений
зв'язок між співвідношеннями (2.2) і (2.3), а також потреба в нетривіальній
умові
. Дуже цікавий обернений
зв'язок між співвідношеннями (2.2) і (2.3), а також потреба в нетривіальній
умові 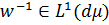 пояснюється
встановленням двоїстості між
пояснюється
встановленням двоїстості між 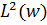 та
та 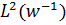 як Банахових просторів
(див. [9], [2]). Відмітимо, що доповнення
як Банахових просторів
(див. [9], [2]). Відмітимо, що доповнення
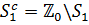 із
із 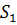 в
в 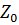 еквівалентно півосі
еквівалентно півосі 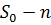 , де
, де 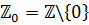 . Отже, загальна і більш
складна проблема прогнозування на основі
. Отже, загальна і більш
складна проблема прогнозування на основі 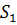 в
в 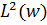 була зведена до
звичайної проблеми прогнозування в
була зведена до
звичайної проблеми прогнозування в 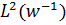 . В цілому, для
будь-якого набору індексів
. В цілому, для
будь-якого набору індексів 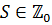 із скінченним числом точок із
із скінченним числом точок із 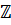 добавлених чи
відібраних, нехай
добавлених чи
відібраних, нехай 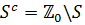 буде доповненням
буде доповненням 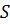 до
до 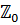 , і для фіксованого
, і для фіксованого 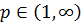 , визначимо
, визначимо 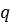 та
та 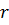 наступною рівністю:
наступною рівністю:
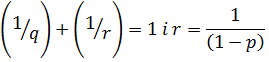
відповідно. Тоді той же аргумент двоїстості
показує, що
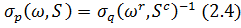
якщо 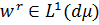 . Хоча останнє
нетривіальне обмеження може бути послаблене [2], до
. Хоча останнє
нетривіальне обмеження може бути послаблене [2], до 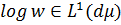 , але величина
, але величина 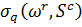 , можливо, не буде чітко визначена. На щастя, для
набору
, можливо, не буде чітко визначена. На щастя, для
набору 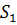 ця складність була
усунута в [2, Теорема 3], використовуючи іншу задачу екстремальної двоїстості в
[3], пов’язану з проекцією
ця складність була
усунута в [2, Теорема 3], використовуючи іншу задачу екстремальної двоїстості в
[3], пов’язану з проекцією 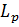 на простір Харді
на простір Харді 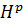 . Тим не менш, для
загального
. Тим не менш, для
загального 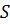 , визначення правої частини рівності (2.4)
залишається відкритим питанням. В ідеалі хотілося б застосувати (2.4), коли
одна проблема простіша, ніж інша, однак (2.4) не має сенсу, коли проблеми
прогнозування, що відповідають
, визначення правої частини рівності (2.4)
залишається відкритим питанням. В ідеалі хотілося б застосувати (2.4), коли
одна проблема простіша, ніж інша, однак (2.4) не має сенсу, коли проблеми
прогнозування, що відповідають 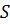 та
та 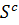 мають однакову
складність або ж навіть ідентичні. У попередньому випадку, підходяща
ортогоналізація у поєднанні з (2.4), здається, забезпечує гарний метод для
розв’язку деяких проблем прогнозування. Наприклад, для
мають однакову
складність або ж навіть ідентичні. У попередньому випадку, підходяща
ортогоналізація у поєднанні з (2.4), здається, забезпечує гарний метод для
розв’язку деяких проблем прогнозування. Наприклад, для 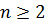 доповнення
доповнення 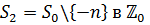 еквівалентно
еквівалентно 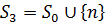 , що відповідає вилученню
і приєднанню одного спостереження в
, що відповідає вилученню
і приєднанню одного спостереження в 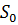 відповідно. Жодна з
проблем не є тривіальною, але останнє здається простіше. В [2, теореми 5, 6]
метод ортогоналізації використовується для обчислення
відповідно. Жодна з
проблем не є тривіальною, але останнє здається простіше. В [2, теореми 5, 6]
метод ортогоналізації використовується для обчислення 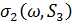 . Тоді співвідношення
двоїстості (2.4) використовується для визначення
. Тоді співвідношення
двоїстості (2.4) використовується для визначення 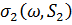 , що дає:
, що дає:
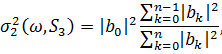
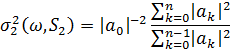
В цьому пункті ми обчислюємо 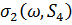 для більш загального
набору індексів
для більш загального
набору індексів 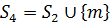 з
з 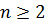 і
і 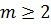 , тобто
, тобто
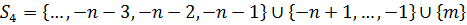
Цей набір індексів має властивості як 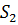 так і
так і 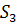 . Насправді, він
зводиться до
. Насправді, він
зводиться до 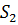 , коли
, коли 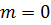 , в той час як його
доповнення
, в той час як його
доповнення 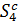 в
в 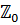 має той же вигляд, як і
має той же вигляд, як і 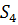 , так, що відношення
двоїстості (2.4) не має сенсу. Тут також показано, що метод ортогоналізації,
головним кроком якого є визначення проекції
, так, що відношення
двоїстості (2.4) не має сенсу. Тут також показано, що метод ортогоналізації,
головним кроком якого є визначення проекції 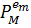 з
з 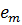 на підпростір
на підпростір 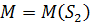 , може бути використаний
для вирішення проблеми. Щоби встановити значення, позначимо ортогональну
проекцію
, може бути використаний
для вирішення проблеми. Щоби встановити значення, позначимо ортогональну
проекцію 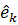 на підпростір
на підпростір 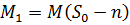 . Оскільки
. Оскільки 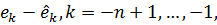 ортогональні до
ортогональні до 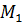 , то підпростори
, то підпростори 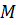 і
і 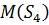 можна записати у вигляді
наступних ортогональних сум:
можна записати у вигляді
наступних ортогональних сум:
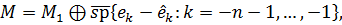
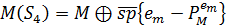
Таким чином, обчислення 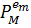 , його проекції та норми являється першочерговим. Наступна
тотожність, яка являє собою узагальнення [2, теорема 6], представляє окремий
інтерес. Власне, цікавий її зв’язок з
, його проекції та норми являється першочерговим. Наступна
тотожність, яка являє собою узагальнення [2, теорема 6], представляє окремий
інтерес. Власне, цікавий її зв’язок з 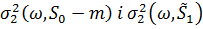 , де
, де 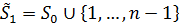 (з
(з 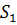 , де
, де 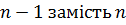 ):
):
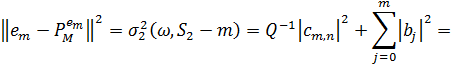
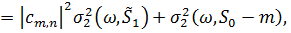 (2.7)
(2.7)
Де 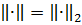 i
i
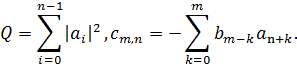
Константа 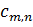 насправді являється
коефіцієнтом
насправді являється
коефіцієнтом 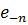 у формальному розкладі в ряд
у формальному розкладі в ряд 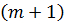 -го кроку прогнозу
-го кроку прогнозу 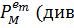 . [16]). Наостанок, бажана відстань:
. [16]). Наостанок, бажана відстань:
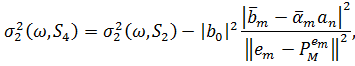
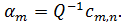
На відміну від (2.2), (2.3) і (2.5), де відстань
залежить або ж лише від 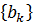 або лише від
або лише від 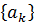 , у випадку (2.7) і (2.9)
одночасно залежить від обох. Явні вирази цих відстаней забезпечують корисні
інструменти для оцінки впливу додавання (вилучення) вектора на зниження
(підвищення) таких відстаней. А саме, як слідує з (2.7), видалення
, у випадку (2.7) і (2.9)
одночасно залежить від обох. Явні вирази цих відстаней забезпечують корисні
інструменти для оцінки впливу додавання (вилучення) вектора на зниження
(підвищення) таких відстаней. А саме, як слідує з (2.7), видалення 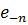 із
із 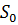 не буде збільшувати
відстань від
не буде збільшувати
відстань від 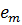 з
з 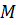 якщо
якщо 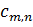 рівне нулю. Аналогічно з
(2.9), додавання
рівне нулю. Аналогічно з
(2.9), додавання 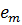 до
до 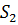 не зменшить
не зменшить 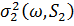 якщо
якщо 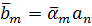 . Ці факти швидше за все
мають цікаву інтерпретацію результатів у статистиці (див. [16], [14]). Було б
корисно привести кілька конкретних прикладів оціночних функцій
. Ці факти швидше за все
мають цікаву інтерпретацію результатів у статистиці (див. [16], [14]). Було б
корисно привести кілька конкретних прикладів оціночних функцій 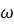 або ж стаціонарних
процесів, які відображають ці феномени.
або ж стаціонарних
процесів, які відображають ці феномени.
.7
Результати і доведення для 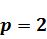
В цьому розділі для комплексно значної матриці 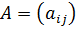 , ми писатимемо
, ми писатимемо 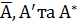 для матриць
для матриць 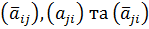 відповідно.
Використовуючи зовнішню функцію
відповідно.
Використовуючи зовнішню функцію 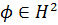 , ми визначаємо
, ми визначаємо 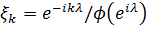 , де
, де 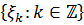 це повний ортонормований
базис
це повний ортонормований
базис 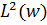 такий, що
такий, що
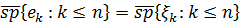
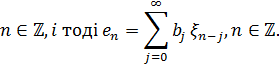
Ми виражаємо різні проекції в термінах 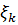 .
.
Теорема 3.1
Покладемо w - невід’ємна інтегрована функція з 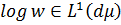 . Тоді матимемо наступне:
. Тоді матимемо наступне:
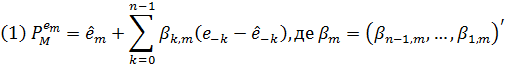
Задовольняє умову (3.3) нижче.
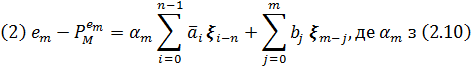
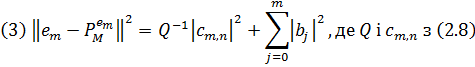
Для 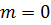 , Теорема 3.1. дає явний
вигляд
, Теорема 3.1. дає явний
вигляд 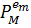 . Він необхідний для
проектування
. Він необхідний для
проектування 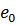 на
на 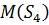 . В силу (2.6), ми також
маємо спроектувати
. В силу (2.6), ми також
маємо спроектувати 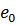 на одновимірний підпростір
на одновимірний підпростір 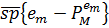 або ж визначити
коефіцієнт
або ж визначити
коефіцієнт
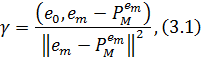
де 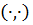 внутрішнім оператором
внутрішнім оператором 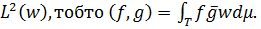 Віповідні результати
наведені в наступній теоремі.
Віповідні результати
наведені в наступній теоремі.
Теорема 3.2
Покладемо w - невід’ємна інтегрована функція з 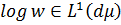 . Тоді мають місце наступні твердження:
. Тоді мають місце наступні твердження:
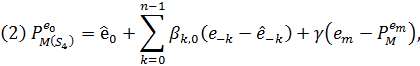
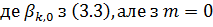
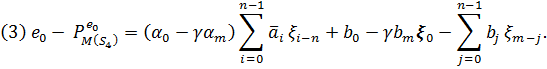
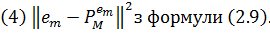
Нехай 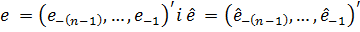 . Для визначення проекції
. Для визначення проекції
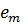 на
на 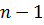 - мірного проміжку
записів
- мірного проміжку
записів 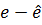 ,
, 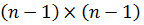 матриці
матриці 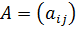 і
і 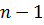 - вектор
- вектор 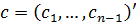 необхідні наступні
компоненти:
необхідні наступні
компоненти:
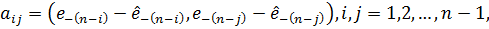
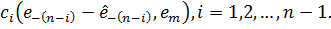
Ми визначимо 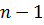 - мірний вектор
- мірний вектор 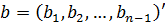 і
і 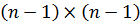 - мірну нижню трикутну
матрицю
- мірну нижню трикутну
матрицю 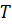 :
:
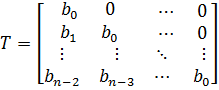
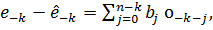
наступне представлення 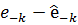 має місце:
має місце:
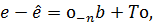
де 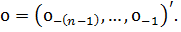 Звідси ми отримуємо
Звідси ми отримуємо
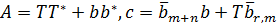
де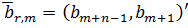 визначено і зсунуто вектор
визначено і зсунуто вектор 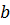 вице. В цих позначеннях,
нормальне рівняння для
вице. В цих позначеннях,
нормальне рівняння для 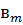 в теоремі 3.1 (1) буде
в теоремі 3.1 (1) буде
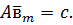
Крім того, ми визначимо 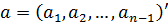 . Тоді в силу (2.1),
(2.8) і (2,10),
. Тоді в силу (2.1),
(2.8) і (2,10),
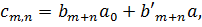
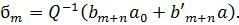
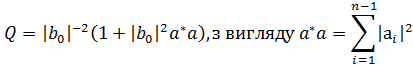
Оскільки матриця А має ранг один збурення 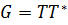 , вона може бути легко інверсована за допомогою оберненої
, вона може бути легко інверсована за допомогою оберненої 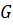 і співвідношення між
і співвідношення між 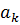 і
і 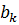 описаним в (2.1).
Обернена матриця матриці А і інші відповідні результати наведені в наступній
лемі.
описаним в (2.1).
Обернена матриця матриці А і інші відповідні результати наведені в наступній
лемі.
Лема 3.3
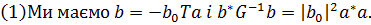
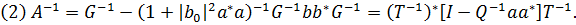
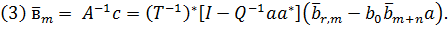
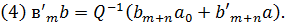
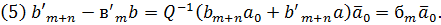
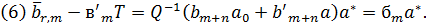
Доведення леми є простим, тому ми його опустимо.
Доведення теореми 3.1.
Виходячи з (3.3) ми вже вище довели (1).
Використовуючи представлення в (3.2) і визначення 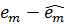 ми маємо
ми маємо
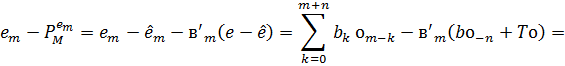
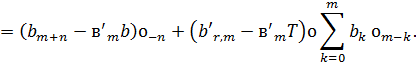
Твердження (2) слідує з леми (3.3) (5), (6). нарешті, ми отримуємо (3)
з (2).
Доведення теореми 3.2.
Використовуючи теорему 3.1 (2) і останню
тотожність в (2.1), ми отримаємо
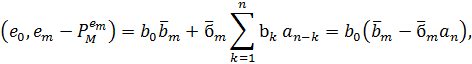
Звідси отримуємо (1). З (2.6) і (3.1), 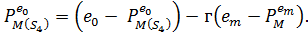
Тоді (2) випливає з теореми (3.1), і (3)
виводиться застосуванням теореми (3.1) (2).
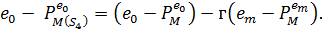
Ця тотожність необхідна для доведення (4). Так 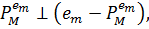
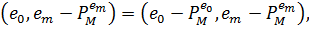
Котре, в силу (3.1) дає
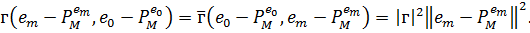
Таким чином
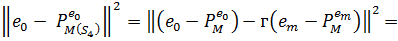
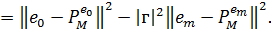
Тепер, 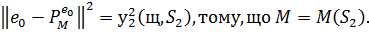 З іншої сторони, з (1)
ми маємо:
З іншої сторони, з (1)
ми маємо:
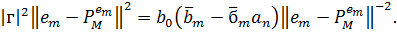
Таким чином, ми отримуємо (4), бажану формулу
відстані (2.9).
Звичайно, це являє собою великий інтерес для
обчислення 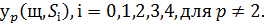 Для і=0
Для і=0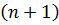 - й крок проблема
прогнозування була вирішена в [1], [10] з додатковою гіпотезою, що
- й крок проблема
прогнозування була вирішена в [1], [10] з додатковою гіпотезою, що
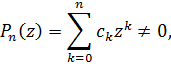
Для всіх 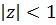 , де коефіцієнти
, де коефіцієнти 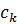 визначаються наступним
чином:
визначаються наступним
чином:
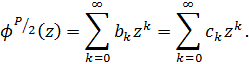
Використовуючи цей результат і співвідношення
двоїстості (2.4), 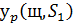 знаходиться в [2]. Здається, цілком імовірно, що
одномірний метод ортогоналізації який використовується в [2, теорема 5], може
бути продовжений до
знаходиться в [2]. Здається, цілком імовірно, що
одномірний метод ортогоналізації який використовується в [2, теорема 5], може
бути продовжений до 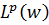 , а потім за допомогою відношення двоїстості
(2.4), можна також обчислити
, а потім за допомогою відношення двоїстості
(2.4), можна також обчислити 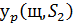 . Вздовж цього розширення набору індексів
. Вздовж цього розширення набору індексів 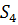 може знадобитися
припущення про місце нулів
може знадобитися
припущення про місце нулів 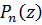 впродовж кількох n, що піднімає питання про
існування нетривіальних вагових функцій
впродовж кількох n, що піднімає питання про
існування нетривіальних вагових функцій 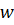 , які задовольняють ці умови.
, які задовольняють ці умови.
2. Основні результати
.1 Перевірка гіпотези про двоїстість та ортогоналізацію
Приклад 1
Розглянемо спектральну щільність виду 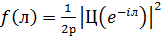
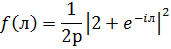
Маємо 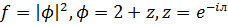 . Звідси можемо одразу
визначити коефіцієнти
. Звідси можемо одразу
визначити коефіцієнти 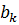 :
: 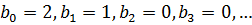
Для визначення коефіцієнтів 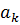 розглянемо розклад виду
розглянемо розклад виду
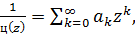 тобто перепишемо нашу щільність
тобто перепишемо нашу щільність
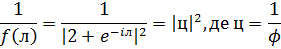
Подамо у вигляді суми геометричної прогресії 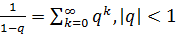 , звівши до відповідного
вигляду отримаємо
, звівши до відповідного
вигляду отримаємо
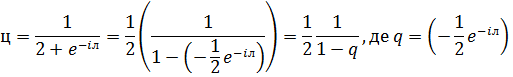
Підставимо у праву частину рівності замість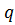
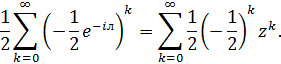
Тепер легко можна записати коефіцієнти 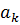
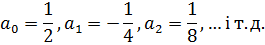
Перевіримо виконання умов 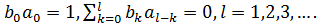
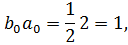
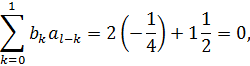
Тепер знайдемо стандартне відхилення для набору
індексів
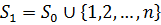
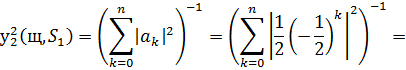
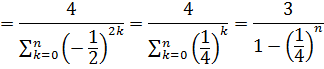
Для множини 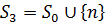
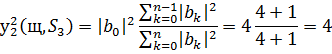
Стандартне відхилення для набору 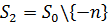 матиме вигляд
матиме вигляд
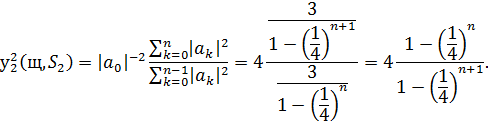
Приклад 2
Розглянемо тепер щільність виду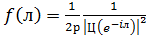 , а саме
, а саме
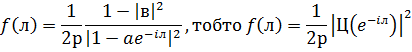
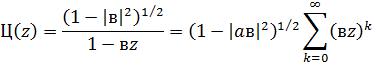
Проведемо ту ж саму процедуру визначення
коефіцієнтів 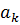 і
і 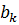 :
: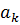 :
:
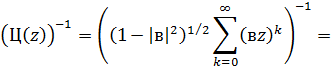
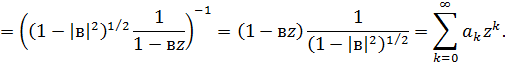
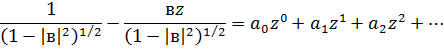
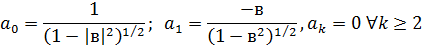
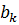 :
:
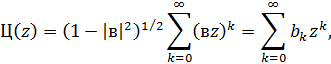
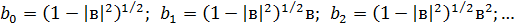
Перевіримо виконання умов 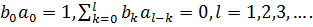
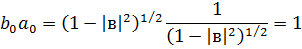
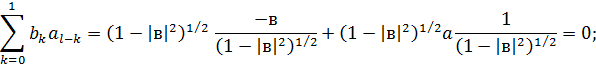
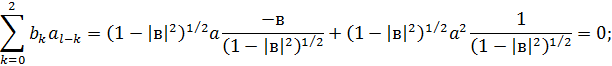
Стандартні відхилення у цьому випадку будуть
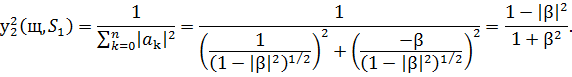
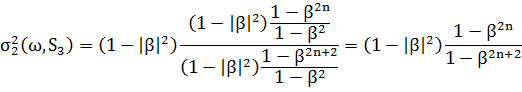
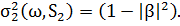
Висновок
В даній роботі були розглянуті основні проблеми
та гіпотези задач прогнозу стаціонарних випадкових послідовностей (у широкому
сенсі), спектральний розклад кореляційної функції та спектральне представлення
стаціонарних регулярних послідовностей і. У роботі досліджено задачу пошуку
обґрунтованої загальної індексної множини S, яка проливає світло на труднощі
при обчисленні 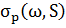 для
для 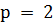 , розглянуто два приклади
застосувань теорії для гіпотез про двоїстість та ортогонлізацію, а саме дві
спектральні щільності з прямим та оберненим способом відшукання коефіцієнтів
ряду Фур’є, знайдено вирази для знаходження коефіцієнтів
, розглянуто два приклади
застосувань теорії для гіпотез про двоїстість та ортогонлізацію, а саме дві
спектральні щільності з прямим та оберненим способом відшукання коефіцієнтів
ряду Фур’є, знайдено вирази для знаходження коефіцієнтів 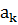 та
та 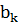 , перевірено виконання
умов регулярності, знайдено значення величин стандартних відхилень для наборів
індексів
, перевірено виконання
умов регулярності, знайдено значення величин стандартних відхилень для наборів
індексів 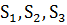 .
.
Література
1. S. Cambanis and A.R. Soltani, Prediction of stable processes: Spectral and moving average
representations, Z. Wahrsch. Verw. Gebiete 66 (1984), 593-612. MR0753815
(86g:60054)
. R. Cheng, A.G. Miamee and M. Pourahmadi, Some extremal
problems in 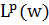 , Proc. Amer. Math. Soc.126 (1998), 2333-2340.
MR1443377 (98j:42003)
, Proc. Amer. Math. Soc.126 (1998), 2333-2340.
MR1443377 (98j:42003)
. P.L. Duren, Theory of 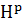 Spaces, Academic Press, New York, 1970.
MR0268655 (42:3552)
Spaces, Academic Press, New York, 1970.
MR0268655 (42:3552)
. M. Frank and L. Klotz, A duality method
in prediction theory of multivariate stationary sequences, Math. Nachr.244 (2002),
64-77. MR1928917 (2003m:60105)
. T.W. Gamelin, Uniform Algebras, Prentice-Hall, Englewood Cliffs, N.J., 1969.
MR0410387 (53:14137)
6. L. Klotz and M. Riedel, Some remarks on
duality of stationary sequences, Colloq. Math. 86 (2000), 225-228. MR1899439
(2003b:60050)
. A.N. Kolmogorov, Stationary sequences in a Hilbert space, Bull. Moscow State
University 2 (1941), 1-40.
. A.G. Miamee, On basicity of exponentials in 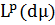 and general prediction problems,
Period. Math. Hungar. 26 (1993), 115-124. MR1230571 (94k:60066)
and general prediction problems,
Period. Math. Hungar. 26 (1993), 115-124. MR1230571 (94k:60066)
. A.G. Miamee and M. Pourahmadi, Best
approximation in 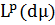 and prediction problems of Szego, Kolmogorov,
Yaglom and Nakazi, J. London Math. Soc. 38 (1988), 133-145. MR0949088
(90g:60042)
and prediction problems of Szego, Kolmogorov,
Yaglom and Nakazi, J. London Math. Soc. 38 (1988), 133-145. MR0949088
(90g:60042)
. T. Nakazi, Two problems in prediction
theory, Studia Math. 78 (1984), 7-14. MR0766702 (86i:60122)
. T. Nakazi and K. Takahashi,
Predictionnunits of time ahead, Proc. Amer. Math. Soc. 80 (1980), 658-659.
MR0587949 (82b:60041)
. M. Pourahmadi, Taylor expansi on 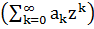 and some applications,
Amer. Math. Monthly 91 (1984), 303-307. MR0740245 (85e:30003)
and some applications,
Amer. Math. Monthly 91 (1984), 303-307. MR0740245 (85e:30003)
. M. Pourahmadi, Two prediction problems
and extensions of a theorem of Szego, Bull. Iranian Math. Soc.19 (1993), 1-12.
MR1289507 (95j:60061)
. M. Pourahmadi, Foundations of Prediction
Theory and Time Series Analysis, John Wiley, New York, 2001. MR1849562
(2002f:62090)
. K. Urbanik, A duality principle for
stationary random sequences, Colloq. Math. 86 (2000), 153-162. MR1808671
(2001j:60072)
. N. Wiener and P.R. Masani, The prediction theory of multivariate stationary processes.II,
Act. Math. 99 (1958), 93-137. MR0097859 (20:4325)
. А.Н. Ширяев, Вероятность, Москва «наука»,
главная редакция физико-математической литературы - 1989