Аксиоматика теории множеств
Введение
Значение математической
логики в нашем и прошлом столетии сильно возросло. Главной причиной этого
явилось открытие парадоксов теории множеств и необходимость пересмотра
противоречивой интуитивной теории множеств. Было предложено много различных аксиоматических
теорий для обоснования теории множеств, но как бы они не отличались друг от
друга своими внешними чертами, общее для всех них содержание составляют те
фундаментальные теоремы, на которые в своей повседневной работе опираются
математики. Выбор той или иной из имеющихся теорий является в основном делом
вкуса; мы же не предъявляем к системе, которой будем пользоваться, никаких
требований, кроме того, чтобы она служила достаточной основой для построения
современной математики.
§1. Система аксиом
Опишем теорию первого
порядка NBG, которая в основном является
системой того же типа, что и система, предложенная первоначально фон Нейманом
[1925], [1928], а затем тщательно пересмотренная и упрощенная Р. Робинсоном
[1937], Бернайсом [1937—1954] и Гёделем [1940]. (Будем в основном следовать
монографии Гёделя, хотя и с некоторыми важными отклонениями.) Теория NBG имеет единственную предикатную букву
 и не имеет ни одной функциональной буквы
или предметной константы. Чтобы быть ближе к обозначениям Бернайса [1937—1954]
и Гёделя [1940], мы будем употреблять в качестве переменных вместо x1, x2, … прописные латинские буквы X1, Х2, ... (Как обычно, мы используем буквы X, Y, Z, ... для обозначения произвольных переменных.) Мы введем также сокращенные
обозначения Х
и не имеет ни одной функциональной буквы
или предметной константы. Чтобы быть ближе к обозначениям Бернайса [1937—1954]
и Гёделя [1940], мы будем употреблять в качестве переменных вместо x1, x2, … прописные латинские буквы X1, Х2, ... (Как обычно, мы используем буквы X, Y, Z, ... для обозначения произвольных переменных.) Мы введем также сокращенные
обозначения Х Y для
Y для (X, Y) и X
(X, Y) и X Y для
Y для 
 (X, Y). Содержательно знак
(X, Y). Содержательно знак  понимается
как символ отношения принадлежности.
понимается
как символ отношения принадлежности.
Следующим образом
определим равенство:
Определение. Х=Y служит сокращением для формулы  .
.
Таким образом, два
объекта равны тогда и только тогда, когда они состоят из одних и тех же
элементов.
Определение.  служит
сокращением для формулы
служит
сокращением для формулы  (включение).
(включение).
Определение. X Y служит сокращением для Х
Y служит сокращением для Х  Y & X ≠ Y (собственное включение).
Y & X ≠ Y (собственное включение).
Из этих определений легко
следует
Предложение 1.
(а)  Х
= Y
Х
= Y
 (X
(X
 Y
&
Y
Y
&
Y
 X);
X);
(b)
 Х = Х;
Х = Х;
(с)  Х
= Y
Х
= Y
 Y
=
Х;
Y
=
Х;
(d)
 Х = Y
Х = Y
 (Y
= Z
(Y
= Z
 Х
= Z);
Х
= Z);
(е)  Х
= Y
Х
= Y
 (Z
(Z X
X
 Z
Z Y).
Y).
Теперь приступим к
перечислению собственных аксиом теории NBG, перемежая формулировки самих аксиом различными
следствиями из них и некоторыми дополнительными определениями. Предварительно,
однако, отметим, что в той «интерпретации», которая здесь подразумевается,
значениями переменных являются классы. Классы — это совокупности, соответствующие
некоторым, однако отнюдь не всем, свойствам (те свойства, которые фактически
определяют классы, будут частично указаны в аксиомах. Эти аксиомы обеспечивают
нам существование необходимых в математике классов и являются, достаточно
скромными, чтобы из них нельзя было вывести противоречие). (Эта «интерпретация»
столь же неточна, как и понятия «совокупность», «свойство» и т. д.)
Назовем класс множеством,
если он является элементом какого-нибудь класса. Класс, не являющийся
множеством, назовем собственным классом.
Определение. M(X) служит сокращением для  Y(X
Y(X Y) (X есть множество).
Y) (X есть множество).
Определение. Pr(X) служит сокращением для  M(X)
(X есть собственный класс).
M(X)
(X есть собственный класс).
В дальнейшем увидим, что
обычные способы вывода парадоксов приводят теперь уже не к противоречию, а
всего лишь к результату, состоящему в том, что некоторые классы не являются
множествами. Множества предназначены быть теми надежными, удобными классами,
которыми математики пользуются в своей повседневной деятельности; в то время
как собственные классы мыслятся как чудовищно необъятные собрания, которые,
если позволить им быть множествами (т. е. быть элементами других классов), порождают
противоречия.
Система NBG задумана как теория, трактующая о
классах, а не о предметах. Мотивом в пользу этого послужило то обстоятельство,
что математика не нуждается в объектах, не являющихся классами, вроде коров
или молекул. Все математические объекты и отношения могут быть выражены в
терминах одних только классов. Если же ради приложений в других науках
возникает необходимость привлечения «неклассов», то незначительная модификация
системы NBG позволяет применить ее равным
образом как к классам, так и к «неклассам» (Мостовский [1939]).
Мы введем строчные
латинские буквы x1, x2, … в качестве специальных, ограниченных
множествами, переменных. Иными словами,  x1 A (x1) будет служить
сокращением для
x1 A (x1) будет служить
сокращением для  X (M(X)
X (M(X) A (X)) , что содержательно имеет следующий
смысл: «A истинно для всех множества, и
A (X)) , что содержательно имеет следующий
смысл: «A истинно для всех множества, и  x1 A (x1) будет
служить сокращением для
x1 A (x1) будет
служить сокращением для  X (M(X)
X (M(X) A (X)), что содержательно имеет смысл: «A истинно для некоторого множества». Заметим, что употребленная в этом
определении переменная X
должна быть отличной от переменных, входящих в A (x1). (Как и
обычно, буквы х, y, z, ... будут употребляться для обозначения
произвольных переменных для множеств.)
A (X)), что содержательно имеет смысл: «A истинно для некоторого множества». Заметим, что употребленная в этом
определении переменная X
должна быть отличной от переменных, входящих в A (x1). (Как и
обычно, буквы х, y, z, ... будут употребляться для обозначения
произвольных переменных для множеств.)
П р и м е р. Выражение  Х
Х х
х y
y ZA (X, х, y, Z) служит сокращением для
ZA (X, х, y, Z) служит сокращением для
 Х
Х Xj
(М(Xj)
Xj
(М(Xj)
 Y(M(Y)&
Y(M(Y)& ZA
(X, Xj, Y, Z))).
ZA
(X, Xj, Y, Z))).
А к с и о м а Т. (Аксиома объемности.) Х = Y
 (X
(X Z
Z Y
Y Z).
Z).
Предложение 2. Система NBG является
теорией первого порядка с равенством.
А к с и о м а Р. (Аксиома
пары.)  x
x y
y z
z u (u
u (u  z
z  u = x
u = x u = y), т. е. для любых множеств х и у
существует множество z
такое, что х и у являются единственными его элементами.
u = y), т. е. для любых множеств х и у
существует множество z
такое, что х и у являются единственными его элементами.
А к с и о м а N. (Аксиома
пустого множества.)  х
х  y (у
y (у  х), т. е. существует множество, не содержащее никаких
элементов.
х), т. е. существует множество, не содержащее никаких
элементов.
Из аксиомы N и аксиомы
объемности следует, что существует лишь единственное множество, не содержащее
никаких элементов, т. е.

 1x
1x  y (у
y (у  х). Поэтому мы можем ввести предметную
константу 0, подчиняв ее следующему условию.
х). Поэтому мы можем ввести предметную
константу 0, подчиняв ее следующему условию.
Определение.  y (y
y (y  0).
0).
Так как выполнено условие
единственности для неупорядоченной пары, то можем ввести новую функциональную
букву g(х, y) для обозначения неупорядоченной пары х и у.
Впрочем вместо g(х, y) мы будем писать {х, у}. Заметим, что можно
однозначно определить пару {X, Y} для любых двух классов Х и Y, а не только для множеств х и у.
Положим {X, Y} = 0, если
один из классов X, Y не является множеством. Можно доказать, что
 NBG
NBG  1Z((M(X)&M(Y)&
1Z((M(X)&M(Y)& u (u
u (u  Z
Z  u = X
u = X  u = Y))
u = Y)) 
 ((
((  M(X)
M(X) 
 M(Y))&Z=0)).
M(Y))&Z=0)).
Этим оправдано введение пары {X, Y}:
Определение.
(М(Х) & М(Y)
& u
(и
u
(и
 {X,
Y}
{X,
Y}  u
= X
u
= X
 u
= Y))
u
= Y)) 
 ((
(( M(X)
M(X)
 M(Y))
& {X, Y}
= 0).
M(Y))
& {X, Y}
= 0).
Можно
доказать, что  NBG
NBG
 x
x
 y
y
 u
(u
u
(u
 {х,
у}
{х,
у}
 u
= x
u
= x
 u
= y) и
u
= y) и
 NBG
NBG
 x
x
 y
(M({х, у})).
y
(M({х, у})).
Определение.  =
{{Х}, {X, Y}}.
=
{{Х}, {X, Y}}.  называется
упорядоченной парой классов Х и Y.
называется
упорядоченной парой классов Х и Y.
Никакого внутреннего
интуитивного смысла это определение не имеет. Оно является лишь некоторым удобным
способом (его предложил Ку-ратовский) определить упорядоченные пары таким
образом, чтобы можно было доказать следующее предложение, выражающее характеристическое
свойство упорядоченных пар.
Предложение 3.
 NBG
NBG  x
x  y
y  u
u  v (
v ( ).
).
Доказательство. Пусть  =
=  .
Это значит, что {{x}, {x, y}} = {{u}, {u, v}}. Так как {х}
.
Это значит, что {{x}, {x, y}} = {{u}, {u, v}}. Так как {х}  {{x}, {x, y}}, то {x}
{{x}, {x, y}}, то {x}  {{u}, {u, v}}. Поэтому {x} = ={u} или {х} = {u, v}. В обоих случаях х = и. С
другой стороны, {u, v}
{{u}, {u, v}}. Поэтому {x} = ={u} или {х} = {u, v}. В обоих случаях х = и. С
другой стороны, {u, v}  {{u}, {u, v}} и, следовательно, {u, v}
{{u}, {u, v}} и, следовательно, {u, v}  {{x}, {x, y}}. Отсюда {u, v} = {x} или {u, v} = ={x, y}. Подобным же образом {x, y} = {u}
или {х, у}={и, v}. Если или {u, v} = ={x} и {х, y} = {u}, то х = и = у = v, в противном
случае {и, v} = {х, у} и,
следовательно, {и, v} = {u, у}. Если при этом v ≠ u, то y
= v, если же v = u,
то тоже y = v. Итак, в любом случае, y = v.
{{x}, {x, y}}. Отсюда {u, v} = {x} или {u, v} = ={x, y}. Подобным же образом {x, y} = {u}
или {х, у}={и, v}. Если или {u, v} = ={x} и {х, y} = {u}, то х = и = у = v, в противном
случае {и, v} = {х, у} и,
следовательно, {и, v} = {u, у}. Если при этом v ≠ u, то y
= v, если же v = u,
то тоже y = v. Итак, в любом случае, y = v.
Мы теперь обобщим понятие
упорядоченной пары до понятия упорядоченной n-ки.
Определение
 =
Х,
=
Х,

Так, например,
 и
и 
В дальнейшем индекс NBG в записи  NBG опускается.
NBG опускается.
Нетрудно доказать следующее
обобщение предложения 3:


Аксиомы существования
классов.
Эти аксиомы утверждают,
что для некоторых свойств, выраженных формулами, существуют соответствующие
классы всех множеств, обладающих этими свойствами.
А к с и о м а В1.  X
X  u
u  v (
v (
 X
X  u
u  v) (
v) ( - отношение).
- отношение).
А к с и о м а В2.  X
X  Y
Y  Z
Z  u (u
u (u  Z
Z  u
u  X & u
X & u  Y)
Y)
(пересечение).
А к с и о м а В3.  X
X  Z
Z  u (u
u (u  Z
Z  u
u  X) (дополнение).
X) (дополнение).
А к с и о м а В4.  X
X  Z
Z  u (u
u (u  Z
Z 
 v (
v (
 X)) (область
X)) (область
определения).
А к с и о м а В5.  X
X  Z
Z  u
u  v (
v (
 Z
Z  u
u  X).
X).
А к с и о м а В6.  X
X  Z
Z  u
u  v
v  w (
w (
 Z
Z 
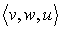
 X).
X).
А к с и о м а В7.  X
X  Z
Z  u
u  v
v  w (
w (
 Z
Z 

 X).
X).
С помощью аксиом В2—В4
можно доказать

 X
X  Y
Y  1Z
1Z  u (u
u (u  Z
Z  u
u  X & u
X & u  Y),
Y),

 X
X  1Z
1Z u (u
u (u  Z
Z  u
u  x),
x),

 X
X  1Z
1Z u (u
u (u  Z
Z 
 v (
v (
 X)).
X)).
Эти результаты
оправдывают введение новых функциональных букв ∩, −, D.
 u (u
u (u  X ∩ Y
X ∩ Y  u
u  X & u
X & u  Y) (пересечение классов Х и Y).
Y) (пересечение классов Х и Y).
 u (u
u (u 

 u
u  X) (дополнение к классу X).
X) (дополнение к классу X).
 u (u
u (u  D (X)
D (X) 
 v (
v (
 X)) (область определения класса
X).
X)) (область определения класса
X).
 (объединение классов Х и Y).
(объединение классов Х и Y).
V =  (универсальный класс).
(универсальный класс).
X − Y = X ∩ 
Общая теорема о
существовании классов.
Предложение 4. Пусть φ (X1,…,Xn,
Y1,…, Ym)
– формула, переменные которой берутся лишь из числа X1,…,Xn,
Y1,…, Ym .
Назовём такую формулу предикативной, если в ней связными являются только
переменные для множеств (т.е. если она может быть приведена к такому виду с
помощью принятых сокращений). Для всякой предикативной формулы φ (X1,…,Xn, Y1,…, Ym)

 Z
Z x1 …
x1 … xn (
xn (
 Z
Z  φ (x1,…,xn, Y1,…, Ym)).
φ (x1,…,xn, Y1,…, Ym)).
Доказательство. Мы можем
ограничиться рассмотрением только таких формул φ, которые не содержат подформул вида Yi  W, так как всякая такая подформула
может быть заменена на
W, так как всякая такая подформула
может быть заменена на  x (x = Yi & x
x (x = Yi & x  W), что в свою очередь эквивалентно формуле
W), что в свою очередь эквивалентно формуле  x (
x ( z (z
z (z  x
x  z
z  Yi) & x
Yi) & x  W). Можно также предполагать, что в φ не содержатся подформулы вида X
W). Можно также предполагать, что в φ не содержатся подформулы вида X X, которые могут быть заменены на
X, которые могут быть заменены на  u (u = X & u
u (u = X & u  X), последнее же эквивалентно
X), последнее же эквивалентно  u (
u ( z (z
z (z  u
u  z
z  X) & u
X) & u  X). Доказательство проведем теперь индукцией по числу k логических связок и кванторов,
входящих в формулу φ (записанную с ограниченными переменными
для множеств).
X). Доказательство проведем теперь индукцией по числу k логических связок и кванторов,
входящих в формулу φ (записанную с ограниченными переменными
для множеств).
1. Пусть k = 0. Формула φ имеет вид xi  xj, или xj
xj, или xj  xi, или xi
xi, или xi  Yi, где 1 ≤ i < j ≤ n. В первом случае, по аксиоме В1, существует некоторый класс W1 такой, что
Yi, где 1 ≤ i < j ≤ n. В первом случае, по аксиоме В1, существует некоторый класс W1 такой, что
 xi
xi xj (
xj (
 W1
W1  xi
xi  xj).
xj).
Во втором случае, по той же аксиоме, существует класс W2 такой, что
 xi
xi xj (
xj (
 W2
W2  xj
xj  xi),
xi),
и тогда, в силу

 X
X Z
Z  u
u  v (
v (
 Z
Z 

 X),
X),
существует класс W3 такой, что
 xi
xi xj (
xj (
 W3
W3  xj
xj  xi).
xi).
Итак, в любом из первых двух случаев
существует класс W3 такой, что
 xi
xi xj (
xj (
 W
W  φ (x1,…,xn,
Y1,…, Ym)).
φ (x1,…,xn,
Y1,…, Ym)).
Тогда, заменив в

 X
X Z
Z  v1…
v1… vk
vk u
u w (
w (
 Z
Z 

 X)
X)
X на W, получим,
что существует некоторый класс Z1
такой, что
 x1…
x1…  xi-1
xi-1 xi
xi xj (
xj (
 Z1
Z1  φ
(x1,…,xn, Y1,…,
Ym)).
φ
(x1,…,xn, Y1,…,
Ym)).
Далее, на основании

 X
X Z
Z  v1…
v1… vm
vm x1…
x1… xn (
xn (

 Z
Z

 X)
X)
там же при Z1 = X,
заключаем, что существует класс Z2
такой, что
 x1 …
x1 …  xi
xi  xi+1 …
xi+1 …  xj (
xj (
 Z2
Z2  φ
(x1,…,xn, Y1,…,
Ym)).
φ
(x1,…,xn, Y1,…,
Ym)).
Наконец, применяя

 X
X Z
Z  v1…
v1… vm
vm x1…
x1… xn (
xn (
 Z
Z 

 X)
X)
(1)
там же при Z2 = Х, получаем, что существует класс Z такой, что
 x1…
x1… xn (
xn (
 Z
Z  φ (x1,…,xn,
Y1,…, Ym)).
φ (x1,…,xn,
Y1,…, Ym)).
Для остающегося случая xi  Yi теорема следует из (1) и
Yi теорема следует из (1) и

 X
X Z
Z  x
x v1…
v1… vm (
vm (
 Z
Z  x
x  X).
X).
2. Предположим, что теорема доказана
для любого k < s и что φ содержит s логических связок и кванторов.
(a) φ
есть  ψ. По индуктивному предположению, существует класс W такой, что
ψ. По индуктивному предположению, существует класс W такой, что
 x1…
x1… xn (
xn (
 W
W  ψ (x1,…,xn,
Y1,…, Ym)).
ψ (x1,…,xn,
Y1,…, Ym)).
Теперь остается положить Z =  .
.
(b) φ
есть ψ  θ. По индуктивному предположению,
существуют классы Z1 и Z2 такие, что
θ. По индуктивному предположению,
существуют классы Z1 и Z2 такие, что
 x1…
x1… xn (
xn (
 Z1
Z1  ψ (x1,…,xn, Y1,…, Ym))
и
ψ (x1,…,xn, Y1,…, Ym))
и
 x1…
x1… xn (
xn (
 Z2
Z2  θ (x1,…,xn,
Y1,…, Ym)).
θ (x1,…,xn,
Y1,…, Ym)).
Искомым классом Z в этом случае будет класс  .
.
(c) φ
есть  x ψ. По индуктивному предположению, существует класс W такой, что
x ψ. По индуктивному предположению, существует класс W такой, что
 x1…
x1… xn
xn x (
x (
 W
W  ψ (x1,…, xn,
x, Y1,…, Ym)).
ψ (x1,…, xn,
x, Y1,…, Ym)).
Применим сперва

 X
X Z
Z  x1 …
x1 …  xn (
xn (
 Z
Z 
 y (
y (
 X)).
X)).
при X =  и получим класс Z1 такой, что
и получим класс Z1 такой, что
 x1 …
x1 …  xn (
xn (
 Z1
Z1
 x
x ψ (x1,…, xn, x, Y1,…,
Ym)).
ψ (x1,…, xn, x, Y1,…,
Ym)).
Теперь положим окончательно Z =  ,
замечая, что
,
замечая, что  x ψ эквивалентно
x ψ эквивалентно

 x
x ψ.
ψ.
Примеры. 1. Пусть φ (X, Y1, Y2) есть формула  u
u v (X =
v (X =  & u
& u 
 Y1 & v
Y1 & v  Y2). Здесь кванторы связывают только переменные для
множеств. Поэтому, в силу теоремы о существовании классов,
Y2). Здесь кванторы связывают только переменные для
множеств. Поэтому, в силу теоремы о существовании классов, 
 Z
Z  x (x
x (x  Z
Z 
 u
u v (x =
v (x =  & u
& u  Y1 & v
Y1 & v  Y2)), а на основании аксиомы объемности,
Y2)), а на основании аксиомы объемности, 
 1Z
1Z  x (x
x (x  Z
Z 
 u
u v (x =
v (x =  & u
& u  Y1 & v
Y1 & v  Y2)). Поэтому возможно следующее
определение, вводящее новую функциональную букву
Y2)). Поэтому возможно следующее
определение, вводящее новую функциональную букву  :
:
Определение.  x (x
x (x  Y1
Y1  Y2
Y2 
 u
u v (x =
v (x =  & u
& u  Y1 & v
Y1 & v 
 Y2)). (Декартово произведение классов Y1 и Y2).
Y2)). (Декартово произведение классов Y1 и Y2).
Определения.
X2 обозначает X  X (в частности, V2 обозначает класс всех упорядоченных
пар).
X (в частности, V2 обозначает класс всех упорядоченных
пар).
…………………………………………………………………………………………………
Xn обозначает Xn-1  X (в частности, Vn обозначает класс всех упорядоченных
n-ок).
X (в частности, Vn обозначает класс всех упорядоченных
n-ок).
Rel(X) служит сокращением для Х 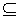 V2 (X есть отношение).
V2 (X есть отношение).
2. Пусть φ (X, Y) обозначает Х 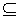 Y. По теореме о существовании классов и на основании
аксиомы объемности,
Y. По теореме о существовании классов и на основании
аксиомы объемности, 
 1Z
1Z x (x
x (x  Z
Z  x
x 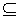 Y). Таким образом, существует класс Z, элементами которого являются все
подмножества класса Y.
Y). Таким образом, существует класс Z, элементами которого являются все
подмножества класса Y.
Определение.  x (x
x (x  P (Y)
P (Y)  x
x 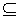 Y). (P (Y): класс всех подмножеств класса Y.)
Y). (P (Y): класс всех подмножеств класса Y.)
3. Рассмотрим в качестве φ (X, Y) формулу  v (X
v (X  v & v
v & v  Y).
Y).
По теореме о
существовании классов и на основании аксиомы объемности, 
 1Z
1Z x (x
x (x  Z
Z 
 v (x
v (x  v & v
v & v  Y)), т.е. существует единственный класс Z, элементами которого являются все элементы элементов
класса Y и только они.
Y)), т.е. существует единственный класс Z, элементами которого являются все элементы элементов
класса Y и только они.
Определение.  x (x
x (x 
 (Y)
(Y) 
 v (x
v (x  v & v
v & v  Y)). (
Y)). ( (Y): объединение всех элементов класса Y)
(Y): объединение всех элементов класса Y)
4. Пусть φ (X) есть  u (X =
u (X =  ). По теореме о существовании классов и на основании
аксиомы объемности, существует единственный класс Z такой, что
). По теореме о существовании классов и на основании
аксиомы объемности, существует единственный класс Z такой, что  x (x
x (x  Z
Z 
 u (x =
u (x =  )).
)).
Определение.  x (x
x (x  I
I 
 u (x =
u (x =  )). (Отношение тождества.)
)). (Отношение тождества.)
Следствие. Для всякой предикативной формулы
φ (X1,…,Xn,
Y1,… …, Ym)

 1W( W
1W( W 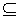 Vn
&
Vn
&  x1…
x1… xn (
xn (
 W
W 
 φ (x1,…,xn,
Y1,…, Ym)).
φ (x1,…,xn,
Y1,…, Ym)).
Доказательство. В силу
предложения 4, существует класс Z, для
которого  x1…
x1… xn (
xn (
 Z
Z  φ (x1,…,xn,
Y1,…, Ym)). Очевидно,
искомым классом W является
класс W = Z ∩ Vn; его единственность вытекает из аксиомы
объемности.
φ (x1,…,xn,
Y1,…, Ym)). Очевидно,
искомым классом W является
класс W = Z ∩ Vn; его единственность вытекает из аксиомы
объемности.
Примеры. 1. Пусть φ есть 
 Y. Обозначим
Y. Обозначим 
 (
(
 Y) сокращенно через
Y) сокращенно через  , тогда
, тогда 

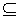 V2 &
V2 &  x1
x1 x2(
x2(
 Y
Y 

 Y). Назовем
Y). Назовем  обратным отношением класса Y.
обратным отношением класса Y.
2. Пусть φ есть  v (
v (
 Y). Обозначим через R(Y) выражение
Y). Обозначим через R(Y) выражение  (
( v (
v (
 Y)). Тогда
Y)). Тогда 
 u (u
u (u  R(Y)
R(Y) 
 v (
v (
 Y)). Класс R(Y) называется областью значений класса Y. Очевидно,
Y)). Класс R(Y) называется областью значений класса Y. Очевидно,  R(Y) = D(
R(Y) = D( ).
).
Заметим, что аксиомы В1 —
В7 являются частными случаями теоремы о существовании классов, т. е.
предложения 4. Иными словами, вместо того, чтобы выдвигать предложение 4 в
качестве схемы аксиом, можно с тем же результатом ограничиться лишь некоторым
конечным числом его частных случаев. Вместе с тем, хотя предложение 4 и позволяет
доказывать существование большого числа самых разнообразных классов, нам, однако,
ничего еще не известно о существовании каких-либо множеств, кроме самых простых
множеств таких, как 0, {0}, {0, {0}}, {{0}} и т. д. Чтобы обеспечить
существование множеств более сложной структуры, введем дальнейшие аксиомы.
А к с и о м а U. (Аксиома объединения.)
 x
x y
y u (u
u (u  y
y 
 v (u
v (u  v & v
v & v  x)).
x)).
Эта аксиома утверждает, что объединение  (х)
всех элементов множества х является также множеством, т. е.
(х)
всех элементов множества х является также множеством, т. е. 
 x
(M(
x
(M( (х))). Множество
и
(х))). Множество
и  (х)
обозначают также через и
(х)
обозначают также через и  v.
v.
Средством порождения
новых множеств из уже имеющихся является образование множества всех подмножеств
данного множества.
А к с и о м а W. (Аксиома множества всех
подмножеств.)
 x
x y
y u (u
u (u  y
y  u
u 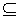 x).
x).
Эта аксиома утверждает,
что класс всех подмножеств множества х есть также множество; его будем
называть множеством всех подмножеств множества х. В силу этой аксиомы, 
 x (M(P (х))).
x (M(P (х))).
Примеры.
 P (0) = {0}.
P (0) = {0}.
 P ({0}) = {0, {0}}.
P ({0}) = {0, {0}}.
 P ({0, {0}}) = {0, {0}, {0, {0}}, {{0}}}.
P ({0, {0}}) = {0, {0}, {0, {0}}, {{0}}}.
Значительно более общим
средством построения новых множеств является следующая аксиома выделения.
А к с и о м а S.
 x
x Y
Y  z
z u (u
u (u  z
z  u
u  x & u
x & u  Y).
Y).
Таким образом, для любого
множества х и для любого класса Y существует множество, состоящее из элементов, общих
для х и Y. Следовательно, 
 x
x Y (M (x ∩ Y)), т. е. пересечение множества с классом есть множество.
Y (M (x ∩ Y)), т. е. пересечение множества с классом есть множество.
Предложение 5. 
 x
x Y (Y
Y (Y 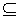 x
x  M (Y)) (т. е. подкласс множества есть множество).
M (Y)) (т. е. подкласс множества есть множество).
Доказательство.

 x
(Y
x
(Y
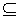 x
x
 Y
∩ x
= Y) и
Y
∩ x
= Y) и

 x
(M
(Y ∩ x)).
x
(M
(Y ∩ x)).
Так как всякая
предикативная формула A(у)
порождает соответствующий класс (предложение 4), то из аксиомы S следует, что для любого множества х
класс всех его элементов, удовлетворяющих данной предикативной формуле A(у), есть множество.
Однако для полного
развития теории множеств потребуется аксиома, более сильная, чем аксиома S. Введем предварительно несколько определений.
Определения
Un (X) означает  x
x y
y z (
z (
 X &
X & 
 X
X  y = z).
y = z).
(X однозначен.)
Fnc (X) означает X 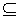 V2 & Un (X). (X есть функция.)
V2 & Un (X). (X есть функция.)
Y
1
X означает
X ∩ (Y
 V).
(Ограничение
Х областью Y.)
V).
(Ограничение
Х областью Y.)
Un1
(X) означает
Un (X)
& Un ( ). (X взаимно
однозначен.)
). (X взаимно
однозначен.)
X‘Y

Если существует
единственное z
такое, что 
 X, то z = X‘y; в противном случае X‘y = 0. Если Х есть функция, а у — множество
из области определения X, то X‘y есть значение этой функции, примененной к у (В
дальнейшем будем по мере необходимости вводить новые функциональные буквы и
предметные константы, как только будет ясно, что соответствующее определение
может быть обосновано теоремой о единственности. В настоящем случае происходит
введение некоторой новой функциональной буквы h с сокращенным обозначением Х‘Y вместо h (X, Y)).
X, то z = X‘y; в противном случае X‘y = 0. Если Х есть функция, а у — множество
из области определения X, то X‘y есть значение этой функции, примененной к у (В
дальнейшем будем по мере необходимости вводить новые функциональные буквы и
предметные константы, как только будет ясно, что соответствующее определение
может быть обосновано теоремой о единственности. В настоящем случае происходит
введение некоторой новой функциональной буквы h с сокращенным обозначением Х‘Y вместо h (X, Y)).
X‘‘Y = R(Y 1 X). (Если Х есть функция, то X‘‘Y есть область значений класса X, ограниченного
областью Y.)
А к с и о м а R. (Аксиома замещения.)
 x (Un (X)
x (Un (X) 
 y
y u (u
u (u  y
y 
 v (
v (
 X & v
X & v  X))).
X))).
Аксиома замещения
утверждает, что если класс Х однозначен, то класс вторых компонент тех
пар из X, первые компоненты которых принадлежать,
является множеством (эквивалентное утверждение: M(R (x 1X))) Из этой аксиомы следует, что если Х
есть функция, то область значений результата ограничения Х посредством
всякой области, являющейся множеством, также есть множество.
Следующая аксиома
обеспечивает существование бесконечных множеств.
А к с и о м а I. (Аксиома
бесконечности.)
 x (0
x (0  x
&
x
&  u (u
u (u  x
x  u
u  {u}
{u}  x)).
x)).
Аксиома бесконечности
утверждает, что существует такое множество х, что 0  x, и если и
x, и если и  x, то и
x, то и  {и} также принадлежит х. Для
такого множества х, очевидно, {0}
{и} также принадлежит х. Для
такого множества х, очевидно, {0}  x, {0, {0}}
x, {0, {0}}  x, {0, {0}, {0, {0}}}
x, {0, {0}, {0, {0}}}  x и т. д. Если теперь положим 1 = {0},
2 = {0, 1}, … , n = {0, 1, … ,
n – 1}, то для любого целого п ≥
0 будет выполнено п
x и т. д. Если теперь положим 1 = {0},
2 = {0, 1}, … , n = {0, 1, … ,
n – 1}, то для любого целого п ≥
0 будет выполнено п  х, и при этом 0 ≠ 1, 0 ≠ 2, 1 ≠ 2, 0 ≠
3, 1 ≠ ≠ 3, 2 ≠ 3, …
х, и при этом 0 ≠ 1, 0 ≠ 2, 1 ≠ 2, 0 ≠
3, 1 ≠ ≠ 3, 2 ≠ 3, …
Список аксиом теории NBG завершен. Видно, что NBG имеет лишь конечное число аксиом, а
именно: аксиому Т (объемности), аксиому Р (пары), аксиому N (пустого множества),
аксиому S (выделения), аксиому U (объединения), аксиому W (множества всех подмножеств),
аксиому R (замещения), аксиому I
(бесконечности) и семь аксиом существования классов В1—В7.
Убедимся теперь в том,
что парадокс Рассела невыводим в NBG. Пусть Y
=  (x
(x  x) ,т. е.
x) ,т. е.  х (х
х (х  Y
Y  х
х  х). (Такой класс Y существует, в силу теоремы о существовании
классов (предложение 4), так как формула х
х). (Такой класс Y существует, в силу теоремы о существовании
классов (предложение 4), так как формула х  х
предикативна.) В первоначальной, т. е. не сокращенной, символике эта последняя
формула записывается так:
х
предикативна.) В первоначальной, т. е. не сокращенной, символике эта последняя
формула записывается так:  X (M(X)
X (M(X)  (X
(X  Y
Y  X
X  X)). Допустим M(Y). Тогда Y
X)). Допустим M(Y). Тогда Y  Y
Y  Y
Y  Y, что, в силу тавтологии (A
Y, что, в силу тавтологии (A 
 A)
A)  A & &
A & &  A, влечет Y
A, влечет Y  Y
Y  Y
Y  Y. Отсюда по теореме дедукции получаем
Y. Отсюда по теореме дедукции получаем  M(Y)
M(Y) (Y
(Y  Y
Y  Y
Y  Y), а затем, в силу тавтологии (B
Y), а затем, в силу тавтологии (B  (A &
(A &  A))
A))
 B , получаем и
B , получаем и  М(Y). Таким образом, рассуждения, с помощью которых обычно
выводится парадокс Рассела, в теории NBG приводят всего лишь к тому результату, что Y есть собственный класс, т. е. не множество. Здесь имеем
дело с типичным для теории NBG
способом избавления от обычных парадоксов (например, парадоксов Кантора и Бурали-Форти).
М(Y). Таким образом, рассуждения, с помощью которых обычно
выводится парадокс Рассела, в теории NBG приводят всего лишь к тому результату, что Y есть собственный класс, т. е. не множество. Здесь имеем
дело с типичным для теории NBG
способом избавления от обычных парадоксов (например, парадоксов Кантора и Бурали-Форти).
Определения
X Irr Y означает  y (y
y (y  Y
Y 

 X) & Rel (X).
X) & Rel (X).
(X есть иррефлексивное отношение на Y.)
X Tr Y означает Rel (X) &  u
u v
v w (u
w (u Y & v
Y & v Y & w
Y & w Y &
Y &
&
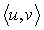
 X
&
X
&
 X
& X
X
& X 

 X).
X).
(X
есть
транзитивное
отношение на Y.)
X Part Y означает
(X Irr Y) & (X Tr Y).
(X
частично
упорядочивает Y.)
X Con Y означает Rel(X) &  u
u v (u
v (u Y & v
Y & v Y & u ≠ v
Y & u ≠ v 
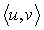

 X
X 

 X).
X).
X Tot Y означает (X Irr Y) & (X Tr Y) & (X Con Y).
(X упорядочивает Y.)
X We Y служит обозначением для Rel(X) & (X Irr Y) &  Z (Z
Z (Z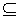 Y &
Y &
& Z ≠ 0 
 y (y
y (y  Z &
Z &  v (v
v (v  Z & v ≠ y
Z & v ≠ y 

 X &
X &
& 
 X))).
X))).
(X вполне упорядочивает Y, т. е. отношение Х иррефлексивно на Y, и всякий непустой подкласс класса Y имеет наименьший в смысле отношения Х
элемент.)
§2.
Аксиома выбора. Лемма Цорна.
Аксиома выбора является
одним из самых знаменитых и наиболее оспариваемых утверждений теории множеств.
Следующие формулы
эквивалентны:
А к с и о м а в ы б о р
а (АС): Для любого множества х существует функция f такая, что для всякого непустого
подмножества у множества х f‘ y  y (такая функция называется в ы б и р а
ю щ е й ф у н к ц и е й для х).
y (такая функция называется в ы б и р а
ю щ е й ф у н к ц и е й для х).
М у л ь т и п л и к а т и
в н а я а к с и о м а (Mult): Для
любого множества х непустых и попарно непересекающихся множеств, существует
множество у
(называемое в ы б и р а ю щ и м м н о ж е с т в о м для х), которое
содержит в точности по одному элементу из каждого множества, являющегося элементом
х.
 u (u
u (u  x
x  u ≠ 0 &
u ≠ 0 &  v (v
v (v  x & v ≠ u
x & v ≠ u  v ∩ u = 0))
v ∩ u = 0))

 y
y u (u
u (u  x
x 
 1w (w
1w (w  u ∩ y)).
u ∩ y)).
П р и н ц и п в п о л н е у п о р
я д о ч е н и я (W. O.): Всякое множество может быть
вполне упорядочено.  x
x  y (y We x).
y (y We x).
Т р и х о т о м и я (Trich):  x
x y (x
y (x  y
y y
y  x).
x).
Л е м м а Ц о р н а (Zorn): Если в частично упорядоченном множестве х всякая
цепь (т. е. всякое упорядоченное подмножество) имеет верхнюю грань, то в х
существует максимальный элемент.
 x
x y ((y Part x) &
y ((y Part x) &  u (u
u (u 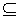 x & y Tot u
x & y Tot u 
 v (v
v (v  x &
x & w (w
w (w  u
u  w =
w =
= v 

 y)))
y))) 
 v (v
v (v  x &
x & w (w
w (w  x
x 

 y))).
y))).
Доказательство.
1.  (W. O.)
(W. O.)  Trich. Пусть даны множества х и у.
Согласно (W. O.), х и у могут быть вполне упорядочены.
Поэтому существуют такие порядковые числа α и β, что х
Trich. Пусть даны множества х и у.
Согласно (W. O.), х и у могут быть вполне упорядочены.
Поэтому существуют такие порядковые числа α и β, что х  α и y
α и y  β. Но так как α
β. Но так как α  β
или β
β
или β  α, то либо x
α, то либо x  y, либо y
y, либо y  x.
x.
3.  (W. O.)
(W. O.)  Mult. Пусть х есть некоторое множество непустых, попарно
непересекающихся множеств. Согласно (W. O.), существует отношение R, вполне упорядочивающее множество
Mult. Пусть х есть некоторое множество непустых, попарно
непересекающихся множеств. Согласно (W. O.), существует отношение R, вполне упорядочивающее множество  (х). Следовательно, существует такая
определенная на х функция f, что f‘u для любого и
(х). Следовательно, существует такая
определенная на х функция f, что f‘u для любого и  х есть наименьший относительно R элемент и. (Заметим, что и
х есть наименьший относительно R элемент и. (Заметим, что и 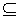
 (х).)
(х).)
4.  Mult
Mult  AC. Для любого множества х
существует функция g такая,
что если и есть непустое подмножество х, то g‘и = u
AC. Для любого множества х
существует функция g такая,
что если и есть непустое подмножество х, то g‘и = u  {и}. Пусть х1 —область
значении функции g. Легко видеть, что х1 является множеством непустых попарно
непересекающихся множеств. На основании Mult, для х1 существует выбирающее
множество у. Отсюда, если 0 ≠ u и u
{и}. Пусть х1 —область
значении функции g. Легко видеть, что х1 является множеством непустых попарно
непересекающихся множеств. На основании Mult, для х1 существует выбирающее
множество у. Отсюда, если 0 ≠ u и u 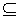 х, то и
х, то и  {и}
{и}  х1 и у содержит и притом единственный элемент
х1 и у содержит и притом единственный элемент из и
из и  {и}. Функция f‘ u = v является искомой выбирающей функцией для х.
{и}. Функция f‘ u = v является искомой выбирающей функцией для х.
5.  АС
АС  Zorn. Пусть у частично
упорядочивает непустое множество х таким образом, что всякая y-цепь в х имеет в х
верхнюю грань. На основании АС, для х существует выбирающая функция f. Рассмотрим произвольный элемент b множества х, и по трансфинитной
индукции определим функцию F
такую, чтобы выполнялось F‘0 = b и F‘α = f‘u для любого α, где u есть множество всех таких верхних граней v множества F‘‘ α относительно упорядочения у, что v
Zorn. Пусть у частично
упорядочивает непустое множество х таким образом, что всякая y-цепь в х имеет в х
верхнюю грань. На основании АС, для х существует выбирающая функция f. Рассмотрим произвольный элемент b множества х, и по трансфинитной
индукции определим функцию F
такую, чтобы выполнялось F‘0 = b и F‘α = f‘u для любого α, где u есть множество всех таких верхних граней v множества F‘‘ α относительно упорядочения у, что v  х и v
х и v  F‘‘ α. Пусть β есть наименьшее порядковое число, которому соответствует
пустое множество верхних граней v множества
F‘‘ β относительно упорядочения v, принадлежащих x и не принадлежащих F‘‘ β. (Порядковые числа, обладающие таким свойством, существуют; в противном
случае функция F была бы
взаимно однозначной с областью определения Оп и с некоторым подмножеством
множества х в качестве области значений, откуда по аксиоме замещения R следовало бы, что Оп есть множество.) Пусть g = β 1 F.
Функция g взаимно однозначна и что если α
<0 γ <0 β, то
F‘‘ α. Пусть β есть наименьшее порядковое число, которому соответствует
пустое множество верхних граней v множества
F‘‘ β относительно упорядочения v, принадлежащих x и не принадлежащих F‘‘ β. (Порядковые числа, обладающие таким свойством, существуют; в противном
случае функция F была бы
взаимно однозначной с областью определения Оп и с некоторым подмножеством
множества х в качестве области значений, откуда по аксиоме замещения R следовало бы, что Оп есть множество.) Пусть g = β 1 F.
Функция g взаимно однозначна и что если α
<0 γ <0 β, то  g‘α,
g‘γ
g‘α,
g‘γ
 y. Поэтому множество g‘‘ β является y-цепью в x. Согласно условию,
и x существует верхняя грань w множества g‘‘ β. Так как множество верхних граней множества F‘‘ β (= g‘‘ β), не содержащихся в g‘‘ β, пусто, то w
y. Поэтому множество g‘‘ β является y-цепью в x. Согласно условию,
и x существует верхняя грань w множества g‘‘ β. Так как множество верхних граней множества F‘‘ β (= g‘‘ β), не содержащихся в g‘‘ β, пусто, то w  g‘‘ β, и, следовательно, w является единственной верхней гранью множества g‘‘ β (ибо всякое множество может содержать в себе не
более одной своей верхней грани). Отсюда следует, что w есть максимальный относительно
упорядочения y элемент
множества х. (Действительно, если
g‘‘ β, и, следовательно, w является единственной верхней гранью множества g‘‘ β (ибо всякое множество может содержать в себе не
более одной своей верхней грани). Отсюда следует, что w есть максимальный относительно
упорядочения y элемент
множества х. (Действительно, если 
 y и z
y и z х, то z
должно быть верхней гранью g‘‘ β, что невозможно.)
х, то z
должно быть верхней гранью g‘‘ β, что невозможно.)
6.  Zorn
Zorn  (W. O.). Пусть z есть множество, а X есть класс всех взаимно однозначных
функций f таких, что D(f)
(W. O.). Пусть z есть множество, а X есть класс всех взаимно однозначных
функций f таких, что D(f) Оп и R(f)
Оп и R(f)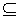 z. Из теоремы Хартогса следует, что X есть множество. Очевидно также, что
0
z. Из теоремы Хартогса следует, что X есть множество. Очевидно также, что
0  X. Отношение
X. Отношение 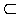 частично
упорядочивает X. Каковы бы
ни были две функции, принадлежащие одной и той же цени в X, одна из них является продолжением
другой. Поэтому для любой цепи в Х объединение всех принадлежащих ей
функций есть снова взаимно однозначная функция, принадлежащая той же цепи. Следовательно,
на основании Zorn, в X имеется максимальный элемент g, представляющий собой взаимно
однозначную функцию, определенную на некотором порядковом числе я и принимающую
значения из z. Допустим,
что z - g‘‘ α
≠ 0. Пусть b
частично
упорядочивает X. Каковы бы
ни были две функции, принадлежащие одной и той же цени в X, одна из них является продолжением
другой. Поэтому для любой цепи в Х объединение всех принадлежащих ей
функций есть снова взаимно однозначная функция, принадлежащая той же цепи. Следовательно,
на основании Zorn, в X имеется максимальный элемент g, представляющий собой взаимно
однозначную функцию, определенную на некотором порядковом числе я и принимающую
значения из z. Допустим,
что z - g‘‘ α
≠ 0. Пусть b z - g‘‘ α, и положим f = g
z - g‘‘ α, и положим f = g {
{ }. Тогда f
}. Тогда f  X и g
X и g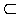 f, что противоречит максимальности g. Следовательно, g‘‘ α
= z, т. е. α
f, что противоречит максимальности g. Следовательно, g‘‘ α
= z, т. е. α  z. Посредством функции g отношение Еα, вполне упорядочивающее
множество α, преобразуется в некоторое отношение, вполне упорядочивающее z.
z. Посредством функции g отношение Еα, вполне упорядочивающее
множество α, преобразуется в некоторое отношение, вполне упорядочивающее z.
Заключение
Система
аксиом теории множеств была создана для решения задачи обоснования базовых
положений современной математики. Таким образом существующие разделы математики
можно считать a priori непротиворечивыми, поскольку все их доказанные высказывания
логически могут быть сведены к аксиомам. В этом отношении аксиоматика выполнила
свое предназначение.
Список
литературы
1. Мендельсон Э. Введение в математическую
логику. – М.: Наука, 1984.
2. Ляпин Е. С. Полугруппы. – М.:
Физматгиз, 1960.
3. Стол Роберт Р. Множества. Логика.
Аксиоматические теории. Пер. с англ. Ю.А. Гастаева и И.Х. Шмаина. Под ред. Ю.А.
Шихановича. М.: «Просвещение», 1968.