Экономико-математические методы и модели в учете

Экономико-математические методы и модели в учете

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

РОССИЙСКАЯ ОТКРЫТАЯ АКАДЕМИЯ ТРАНСПОРТА

Факультет «Экономический»

Кафедра «Учет, анализ и аудит»

КОНТРОЛЬНАЯ РАБОТА

«ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ В УЧЕТЕ»

Выполнил: студент 3-го года

обучения З/О 4 курса

Демкин А. А.

Учебный шифр: 1010-п/БУ-1213

Проверил: Ст. п. З. В. Бабаева

Москва 2013

Задание 1

Составить уравнение модели управления запасами и определить её параметры.

Вариант 3. На некотором станке производятся детали в количестве 2000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 500 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 50 коп. в год за одну деталь. Стоимость производства одной детали составляет 1000 руб. Каким должен быть размер партии деталей, производимой на первом станке, с какой частотой следует запускать производство этих партий, каковы общие затраты?

Модель планирования экономического размера партии

Модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика, можно модифицировать и применять в случае собственного производства продукции. На рис.1 схематично представлен некоторый производственный процесс. На первом станке производится партия деталей с интенсивностью l деталей в единицу времени, которые используются на втором станке с интенсивностью ν, дет./ед. t.

Входные параметры модели планирования экономического размера партии

λ - интенсивность производства продукции первым станком, ед. тов./ед. t;

ν - интенсивность потребления запаса, ед. тов./ед. t;

s - затраты на хранение запаса, руб./ед. тов.· ед. t;

K - затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, руб.;

tп - время подготовки производства (переналадки), ед. t.

Выходные параметры модели планирования экономического размера партии

Q - размер заказа, ед. тов.;

L - общие затраты на управление запасами в единицу времени, руб./ед. t;

τ - период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, ед. t;

h0 - точка заказа, т.е. размер запаса, при котором надо подавать заказ на производство очередной партии, ед. тов.

График циклов изменения запасов в модели планирования экономичного размера партии

-          в течение времени t1 работают оба станка, т.е. продукция производится и потребляется одновременно, вследствие чего запас накапливается с интенсивностью (λ - ν);

-       в течение времени t2 работает только один станок, потребляя накопившийся запас с интенсивностью ν;

Формулы модели экономичного размера партии

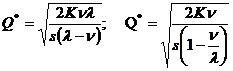
где * - означает оптимальность размера заказа;

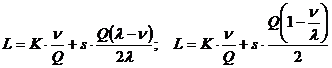
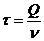
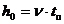
λ=2000 шт./мес.=24000 шт./год

ν=500 шт./мес.=6000 шт./год

s=0,5 руб./год

К=1000 руб.

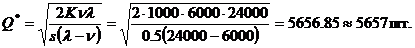
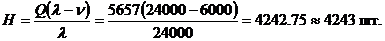
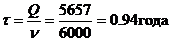
Задание 2

Модель рынка. Модель Вальраса.

Построить модель Вальраса, определить равновесную цену и количество сделок, при которых торговые операции становятся убыточными.

Заданы параметры функции спроса D и функции предложения S, начальная цена P0:

Модель Вальраса - это простейшая модель регулирования рынка через механизм изменения цен. Предложение на рынке S ориентированно на спрос D, S→D, и в идеале должно быть обеспечено равенство предложения и спроса:

Это равенство достигается через цены, которые, если спрос превышает предложение, т.е. D>S, начинают расти до тех пор, пока не будет удовлетворен спрос, т.е. пока D не станет равно S. Если же предложение превышает спрос, т.е. S>D, то цены начинают падать, предложение снижается до тех пор, пока вновь не установится равенство S=D. И процесс повторяется.

Построение модели Вальраса основывается на изучении спроса и предложения на рынке.

Функция спроса D в данной задаче линейная и имеет вид:

=a - APt

где a, A - постоянные параметры,

Pt - цены на момент времени t.

Функция предложения S также линейная и имеет вид:

=b + BPt-1

где b, B - постоянные параметры,

Pt-1 - цены на момент времени t-1.

Траектория изменения цен и количества сделок (модель Вальраса)

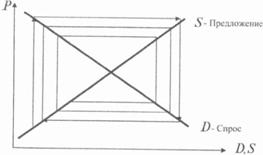
Если при построении функции спроса D ориентируются на текущие цены Pt, то при построении модели предложения S ориентируются на цены предшествующего периода Pt-1, так как сегодняшнее предложение реагирует на цены с некоторым отставанием во времени.

Построение модели начинают с расчета количества предлагаемых сделок (предложений) при заданной цене P0:

1=b + BP0

Зная количество сделок, рассчитывают цену спроса при данном предложении, т.е. спрос приравнивается к предложению Dt=St, из функции спроса:

1=a - AP1

Определяют

1=(a - D1)/A

Затем рассчитывают предложение (количество сделок) следующего периода t2, исходя их цены предшествующего периода t1

2=b + BP1

и цены спроса для t2, принимая, что количество сделок D2=S2

2=(a - D2)/A

Расчет представлен в таблице:

Решение будет закончено, когда цена достигнет равновесия и разница между Pn - Pn-1 станет бесконечно малой величиной ε, т.е. Pt практически будет равна Pt-1:

*=Pt=Pt-1

Значение цены P* называют равновесной ценой.

Задание 3

Найти решение оптимизационной задачи, используя информационную технологию поиска решений.

Вариант 3. На заводе выпускают изделия четырех типов. От реализации 1 ед. каждого изделия завод получает прибыль соответственно 1, 2, 3, 1 д.е. На изготовление изделия расходуются ресурсы трех типов: энергия, материалы, труд. Данные о технологическом процессе представлены в таблице:

Спланируйте производство изделий так, чтобы прибыль от их реализации была наибольшей.

Оптимизационные модели отражают в математической форме смысл экономической задачи. В общем виде математическая постановка задачи линейного программирования (ЗЛП) состоит в определении наибольшего или наименьшего значения целевой функции при заданных ограничениях:

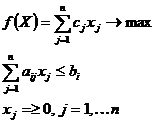
Вектор Х, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, называют планом или допустимым решением ЗЛП.

Microsoft Excel обеспечивает решение задач линейного и нелинейного программирования ограниченной размерности. Модель задачи задается в диалоговом окне Поиск решения. Модель использует целевую функцию, которая записывается в виде формулы в отдельной ячейке. Для целевой функции указывается максимизация, минимизация или равенство фиксированному значению. В процессе поиска решений изменяются значения в указанных ячейках, соответствующих переменным при соблюдении ограничений.

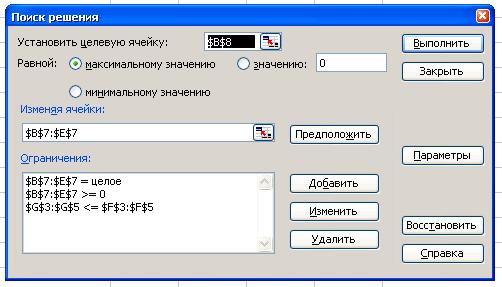
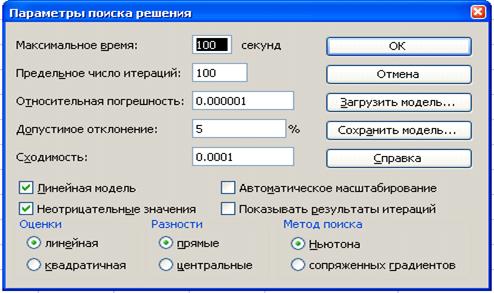
Поиск оптимальной производственной программы по критериям максимума суммарной прибыли. Ограничение - расход ресурсов на выпуск продукции. Задача относится к категории оптимизационных, поскольку допускает множество решений. Выбор оптимального решения выполняется с помощью целевой функции - максимума прибыли. Коэффициенты целевой функции - прибыль на единицу продукции. Ограничения - запас ресурсов, необходимых для изготовления продукции. Дополнительное ограничение на объем выпуска каждого вида продукции (или некоторых их них) - целые числа.

Вывод: производить следует изделия II и III, ни один ресурс не является дефицитным, запас трудовых ресурсов значительно превышает потребности.

Задание 4

экономический планирование равновесный цена

Даны коэффициенты прямых затрат aij и конечный продукт Yi для трехотраслевой экономической системы.

Требуется определить: коэффициенты полных затрат, вектор валового выпуска, условно чистую продукцию. Заполнить схему межотраслевого баланса.

Модель межотраслевого баланса

(модель Леонтьева или модель «затраты - выпуск»)

Указанная модель относится к самым простым вариантам моделей межотраслевого баланса. Алгебраически она сводится к решению системы линейных уравнений, в которых параметрами являются коэффициенты затрат на производство продукции. Рассматривая схему межотраслевого баланса в стоимости выражения по столбцам, можно заметить, что итог материальных затрат любой потребляющей отрасли и её условно чистой продукции равен валовой продукции этой отрасли.

Схема межотраслевого баланса

Вывод можно записать в виде:

 (1)

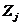 - условно чистая продукция, равная сумме амортизации, оплаты труда и чистого дохода отрасли j;

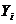 - конечная продукция.

Соотношение (1) охватывает систему из n уравнений, отражающих стоимостной состав продукции всех отраслей. Рассматривая схему по строкам, замечаем, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих её продукцию отраслей и конечной продукции данной отрасли:

 (2)

Уравнения (2) называются уравнениями распределения продукции отраслей материального производства по направлениям использования. Балансовый характер таблицы заключается в том, что:

Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица прямых затрат. Коэффициент прямых затрат показывает, сколько необходимо единиц продукции отрасли i для производства единиц продукции отрасли j, если учитывать только прямые затраты:

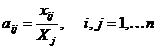 (3)

Подставляя (3) в балансовое соотношение (2), получим:

 (4)

или в матричной форме:

=AX+Y (5)

С помощью этой модели можно выполнять три вида плановых расчетов:

·        задавая для каждой отрасли величины валовой продукции, можно определить величины конечной продукции:

=(E-A)X (6)

·        задавая величины конечной продукции всех отраслей, можно определить величины валовой продукции каждой отрасли:

=(E-A)-1Y (7)

·        задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей - объемы конечной продукции, можно определить величины конечной продукции первых отраслей и объемы валовой продукции вторых.

В формулах (6) и (7) символ Е обозначает единичную матрицу порядка n, а матрицу (Е-А)-1 - матрицу, обратную (Е-А). Обозначим обратную матрицу через В=(Е-А)-1, тогда систему уравнений (7) можно переписать в виде X=BY. Элементы матрицы В называются коэффициентами полных материальных затрат. Они показывают, сколько всего нужно произвести продукции отрасли i для выпуска в сферу конечного использования единицы продукции отрасли j.

Литература

1.       Бережная Е. В., Бережной В.И. Математические методы моделирования экономических систем; Уч. Пособие - М.: Финансы и статистика, 2006.

2.      Левин А.Г., Горбунов Е.А., Орехов Н.А./ Под ред. Н.А Орехова. Математические методы и модели в экономике : Уч. пособие - М:.ЮНИТИ, 2004.

.        Маркин Ю.П. Математические методы и модели в экономике : Уч. пособие - М:. Высшая школа, 2007.