Дослідження систематичного використання історизмів в курсі лекцій з математичного аналізу
Зміст
Вступ
Розділ 1. Теоретичні аспекти
проблеми дослідження
.1 Математичний аналіз як
наука
.2 Математичний аналіз як
навчальний предмет
.3 Діяльнісний підхід до
організації навчально-виховного процесу в педагогічному університеті
Розділ 2. Змістове наповнення
та методика використання історичного матеріалу на лекціях з математичного
аналізу
.1 Ознайомлення студентів з
творцями математичного аналізу
.2 Історичні задачі як засіб
створення проблемних ситуацій на лекціях
.3 Види історичних екскурсів та
їх місце на лекціях
.4 Експериментальна перевірка
результатів дослідження
Висновки
Список використаних джерел
Вступ
Зміст освіти сьогодні - це не тільки
знання, навички і уміння в певній освітній галузі, а й загальнолюдська
культура, яка знаходить вираження в цій галузі. Сучасні тенденції оновлення
змісту освіти передбачають, крім усього іншого, його культуровідповідність,
гуманізацію, гуманітаризацію, інтеграцію й особистісну орієнтацію. Тому
ефективним засобом оновлення змісту математичної освіти у вказаних напрямках
має стати історія математики. А забезпечити культурологічний характер сучасної
математичної освіти покликана історико-методологічна підготовка вчителя
математики.
Історія науки вводить нас у творчу
лабораторію вчених, учить бачити в математиці не суму незмінних правил і догм,
а результат довгих і наполегливих пошуків багатьох поколінь, показує, що за
кожним математичним фактом, за кожною науковою теорією приховані зусилля
конкретних дослідників. Математичні поняття, відношення та теорії завдяки історичній
динамічності стають ближчими і зрозумілішими. Історія математики репрезентує
багатий матеріал про діяльність учених як яскраве свідчення величі їх праці і
наочне підтвердження великої цінності наукового знання. Таке реальне життя
науки, включене до змісту навчальної дисципліни, створює суттєвий вплив
спеціальних математичних знань на психологічну структуру особистості, а загалом
- на формування математичної культури майбутнього вчителя математики.
У процесі вивчення математичного
аналізу, як окремої галузі математики, дуже часто доводиться спиратися на
історико-математичні знання та поняття, які були відкриті або встановлені
багатьма видатними дослідниками. Повідомлення та зауваження
історико-математичного характеру у вивченні різних тем математичного аналізу не
мають на меті підмінити історію математичного аналізу. Вони покликані
торкнутися генезису основних понять, створити у студента загальну орієнтацію в
хронології найважливіших подій з історії аналізу, гуманізувати зміст курсу,
ознайомлюючи слухачів з творцями цієї математичної галузі.
Слід відмітити, що історичні
зауваження органічно вплітаються у лекційний курс математичного аналізу,
оскільки більшість теорем цього курсу - “іменні” теореми.
Отже, приводом до написання роботи
стала необхідність дослідження систематичного використання історизмів в курсі
лекцій з математичного аналізу.
Об’єктом дослідження є математичний
аналіз.
Предметом дослідження є лекційний
курс математичного аналізу.
Гіпотеза дослідження. Систематичне
використання історизмів в курсі лекцій математичного аналізу підвищує інтерес
студентів до цього предмету.
Мета дослідження. З’ясувати, який
історичний матеріал і на якому етапі лекцій з математичного аналізу доцільно
використовувати.
Задачі дослідження:
. Розглянути математичний
аналіз як науку і навчальний предмет.
. З’ясувати функції
історизмів у процесі навчання математичного аналізу.
. Проаналізувати діяльнісний
підхід до організації навчально-виховного процесу в педагогічному університеті.
. Ознайомити студентів з
творцями математичного аналізу.
. Підібрати історичні задачі
як засіб створення проблемних ситуацій на лекціях.
. Експериментально перевірити
результати дослідження.
Для досягнення мети і розв’язання
поставлених завдань були використані такі методи дослідження:
теоретичні - аналіз теоретичного
матеріалу курсу лекцій математичного аналізу; аналіз навчальних програм,
Галузевих стандартів та підручників курсу математичного аналізу;
емпіричні - спостереження, бесіди зі
студентами та викладачами вищих навчальних закладів, аналіз лекційного
матеріалу, підбір історичних задач як засобу створення проблемних ситуацій на
лекціях, анкетування для виявлення рівня зацікавленості студентів; узагальнення
передового педагогічного досвіду; організація і проведення констатуючого, пошукового
та формуючого етапів експерименту для перевірки ефективності розробленої
методичної системи.
Розділ 1. Теоретичні аспекти
проблеми дослідження
.1 Математичний аналіз як наука
Математичний аналіз, як самостійна
галузь науки, почав формуватися із зародження інтегрального та диференціального
числення.
Формування інтегрального та
диференціального числення відбулося на основі операцій з нескінченно малими
величинами в процесі розвитку інтегральних та диференціальних методів і
встановлення тісних зв’язків між ними. Розглянемо джерела виникнення і засоби
творення цих методів, які виникли незалежно один від одного на різних етапах
розвитку математики і довгий час застосовувалися для розв’язування двох різних
груп задач.
Перша група задач зводиться до знаходження
сум нескінченно великого числа нескінченно малих доданків. Це - задачі про
визначення площ, об’ємів, роботи, центрів тяжіння тощо.
Щоб уникнути нескінченності в
обчисленні мір давньогрецький вчений Евдокс запропонував метод вичерпування.
Цей метод плідно розвивали і застосовували Евклід, Архімед та інші математики.
Для знаходження площ і об’ємів
геометричних фігур Архімед використовував методи, які схожі до обчислень
геометричних сум. Наприклад, щоб знайти об’єм тіла обертання, зокрема сфероїда,
Архімед розбивав його на n шарів рівної товщини. Далі розглядав суми об’ємів
циліндрів, описаних навколо кожного із цих шарів і вписаних в них, показував,
що різниця цих сум при збільшенні n стає як завгодно малою. Нарешті, знаходив
об’єм розглядуваного тіла як спільну границю цих сум. У такий спосіб Архімед
розв’язав багато задач, які тепер розв’язуються за допомогою інтегралів [2].
Таким чином, уже антична математика
містила елементи визначеного інтегрування, зокрема, побудову верхніх і нижніх
інтегральних сум, аналогічних певною мірою сумам Дарбу. Метод інтегральних сум
давніх греків спирався на інтуїтивне, строго не визначене поняття площі та
нескінченної суми, а тому застосовувався індивідуально для кожної конкретної
задачі без виділення теоретичних основ.
Метод Архімеда для обчислення площ і
об’ємів дещо спростив і узагальнив італійський математик Л. Валеріо. Йому
вдалось уникнути прикінцевого доведення методом від супротивного за рахунок
використання на інтуїтивному рівні граничного переходу. Він сформулював
загальну теорему і посилався на неї, щоб не проводити щоразу детальні
доведення. Але робота Валеріо “Три книги про центр тяжіння тіл” (1604) не
отримала такої популярності, як роботи Й. Кеплера і Б. Кавальєрі.
Німецький астроном і математик Й.
Кеплер, використовуючи ідеї Архімеда, ще більше звертався до інтуїтивних
прийомів і зовсім не обґрунтовував їх. Щоб обчислити площу якоїсь фігури, він
розбивав її на нескінченну множину нескінченно малих елементів однієї з нею
розмірності. З цих елементів утворював нову фігуру, площу якої вже вмів
обчислювати. Цей метод Й. Кеплер застосовував і до обчислення об’ємів тіл.
Зокрема, вважаючи, що кожне тіло обертання складається з безлічі “найтонших
кружечків”, він визначив об’єми 92 таких тіл.
Ще далі пішов італійський математик
Б. Кавальєрі. Уявляючи кожну фігуру як таку, що складена з “неподільних” -
плоска фігура з відрізків, а тіло з плоских фігур - він сформулював свої
принципи: плоскі фігури і тіла співвідносяться між собою так, як всі їх
неподільні разом взяті; якщо неподільні перебувають в одному і тому ж
відношенні між собою, то відношення площ відповідних фігур чи об’ємів тіл
дорівнює цьому відношенню. Метод неподільних Ю. Кавальєрі мав істотні недоліки,
але сам Кавальєрі вважав ці твердження очевидними і приймав їх без доведення,
як принципи [3].
У першій половині 17 ст. математики
встановили, що велика кількість різнорідних задач з геометрії та механіки мають
спільні шляхи розв’язання і зводяться до квадратур чи кубатур. Ідеї, що містили
елементи визначеного інтегрування, швидко поширювалися серед математиків
Західної Європи. Їх використовували і розвивали Е. Торічеллі, Н. Меркатор, Б.
Паскаль, П. Ферма, Р. Декарт, Х. Гюйгенс, Д. Валліс, І. Барроу. Але на той час
можливості цих методів були обмеженими, бо в кожному конкретному випадку
підраховувалися границі нових інтегральних сум.
До другої групи задач можна віднести
задачі про рухи та інші процеси. Для визначення напрямку руху тіла в деякій
точці його траєкторії потрібне було поняття дотичної. Дослідження кривих
ставили задачі на максимум і мінімум. Вивчення руху взагалі вимагало поняття
миттєвої швидкості. Ці задачі ставилися з давніх часів, але розв’язувалися тоді
геометричними і механічними способами, не пов’язаними спільною ідеєю. Так
Архімед досліджував як побудувати дотичну до спіралі.
Тільки в 17 ст. виявили, що всі ці
задачі можна розв’язувати єдиним методом, використовуючи нескінченно малі
величини. Цей метод отримав розвиток у роботах Р. Декарта, П. Ферма, Д.
Грегорі, Д. Валліса, І. Барроу та інших. Розвиток цього методу привів до
створення диференціального числення.
Найкращі результати на цей час
отримали П. Ферма та І. Барроу. П. Ферма по суті вмів знаходити похідну
довільного многочлена від однієї змінної. Користуючись цим, він показав, як
розв’язувати екстремальні задачі, в тому числі - про вписування в дану кулю
конуса найбільшого об’єму, циліндра найбільшої площі поверхні тощо. Але саме
поняття похідної він не виокремив. Прийоми, розроблені П. Ферма, стали
безпосередніми посередниками диференціального числення. Це відмічали Ж.
Д’Аламбер, Ж. Лагранж і П. Лаплас.
Останнє відкриття, яке
передувало створенню математичного аналізу, зробив І. Барроу. В роботі “Оптичні
і геометричні лекції” (1669-1670) він встановив зв’язок між двома важливими
задачами: обчислення площі і проведення дотичної. Застосовуючи сучасні
позначення, доведене ним твердження можна записати у такому вигляді: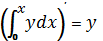 
.
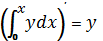Як бачимо, цим самим
встановлено взаємну оберненість операцій диференціювання та інтегрування. До
доведення цієї залежності І. Барроу підійшов двома шляхами: кінематично і
геометрично. Це доведення мало загальний характер: він встановлює і доводить
свої твердження відразу для всіх функцій. Твердження І. Барроу дає можливість
за результатами якого-небудь диференціювання чи інтегрування віднайти результат
застосованої до нього оберненої операції. Використовуючи цей результат він
розв’язав багато обернених задач на дотичні. З його творами ознайомилось багато
вчених, але вони не зрозуміли загальності і важливості цієї залежності через
громіздке геометричне формулювання й уникання аналітичних методів. На
сьогоднішній день залежність, встановлена І. Барроу, є змістом основної теореми
математичного аналізу. Саме вона дає змогу обчислювати інтеграли за допомогою
знаходження первісної, тобто використовуючи операцію обернену до
диференціювання [2].
Основні ідеї математичного
аналізу, щоправда в механічній та геометричній формах, повністю визріли на
кінець 17-го століття. Для остаточного створення інтегрального і
диференціального числення стало необхідним об’єднати існуючі загальні прийоми,
які застосовувалися для розв’язування різних задач, в єдиний метод на базі
поняття нескінченно малої величини і виробити алгоритм для обчислення похідних
та інтегралів. Це стало під силу двом геніальним вченим - І. Ньютону і Г.
Лейбніцу. Їх обох вважають основоположниками диференціального числення.
До основних понять і до
алгоритму числення нескінченно малих І. Ньютон прийшов у середині 60-х років
17-го століття. Перший виклад свого нового аналітичного методу Ньютон записав
восени 1666 року у чорновому нарисі, який мав назву “Наступні пропозиції достатні
для розв’язання задач за допомогою рухів”. Численню нескінченно малих Ньютон
присвятив ще кілька робіт: “Аналіз за допомогою рівнянь з нескінченною
кількістю членів”, “Метод флюксій і нескінченних рядів”. Вони були надруковані
тільки на початку 18 ст., а до публікації мали обмежене поширення.
Погляди І. Ньютона на
числення нескінченно малих кілька разів змінювалися. Спочатку, під впливом
Барроу і Валліса, Ньютон оперував з нескінченно малими величинами, називаючи їх
моментами. Він використовував моменти площ і побудував на їх основі свій метод
квадратури.
року Ньютон встановив чіткий
зв’язок між квадратурами і похідними. Слід відмітити, що на той час у явному
вигляді ще не існувало означення похідної, інтеграла і нескінченно малих
приростів [5].
У 1671 р. І. Ньютон
відмовився від нескінченно малих величин і у праці “Метод флюксій і нескінченні
ряди” увів свій найбільш відомий метод. Він розглядає математичні величини як
“породжувані внаслідок неперервного зростання, подібно до шляху, який описує
тіло або будь-яка річ, що рухається”, і вводить поняття “швидкості породжуючи
їх рухів”. Ці швидкості були названі ним “флюксіями”.
У теорії флюксій І. Ньютон
розв’язував дві основні задачі:
1. Визначення швидкості руху в
даний момент часу за заданим шляхом.
. За заданою швидкістю руху
визначити пройдений за даний час шлях.
Перша задача - диференціювання
функції декількох змінних, які залежать від часу. Розв’язання цієї проблеми
привело Ньютона до обчислення флексії (похідної) від даної елюенти (функції) і
до своєрідного обґрунтування розвинутого ним диференціального числення. Для
розв’язання цієї задачі Ньютон увів спеціальне правило - алгоритм
диференціювання функцій.
Друга задача - інтегрування
диференціального рівняння першого порядку. До неї, зокрема, належать задачі
визначення функції F (вона називається первісною), знаючи її похідну. Саме ця
задача приводить до поняття невизначеного інтеграла.
Використання теореми про взаємну
оберненість операцій диференціювання та інтегрування, знання похідних багатьох
функцій дало Ньютону можливість отримувати флюєнти. Якщо інтеграли
безпосередньо не обчислювались, Ньютон розкладав підінтегральну функцію в
степеневий ряд і інтегрував його почленно. Введення такого прийому - заслуга
Ньютона [2].
Більшість результатів теорії флексій
Ньютон отримав у 60-70 роках 17 ст., але з публікаціями не поспішав. Однією з
причин цього стала недостатня логічна обґрунтованість теорії флексій. Ньютон
шукав методи її обґрунтування і на цьому шляху створив метод перших і останніх
відношень - початкову форму теорії границь. Цей метод він виклав у творі
“Математичні основи натуральної філософії”. Сучасною термінологією твердження
І. Ньютона розкриваються у таких положеннях.
Границя відношення довжини дуги до
довжини хорди є одиниця. Одиниця служить границею відношення довжини дуги до
відрізка дотичної від точки дотику до точки перетину з ординатою другого кінця.
І все ж методи, розроблені Ньютоном,
залишалися недостатніми для обґрунтування диференціального числення. Це був той
етап розвитку аналізу нескінченно малих, коли теорія існує і розвивається, але
не роз’яснюється.
Іншими шляхами прийшов до створення
числення нескінченно малих Г. Лейбніц. В 1672 р. у Парижі він познайомився з Х.
Гюйгенсом, який звернув увагу молодого вченого на математику і, зокрема, на
задачу про визначення суми чисел, обернених трикутним. Так Г. Лейбніц почав
займатися підсумовуванням рядів, яке згодом розглядав як підготовку до
створення диференціального числення. Зустрічі та бесіди з Х. Гюйгенсом показали
Г. Лейбніцу власну необізнаність у новій математиці, і він почав завзято
вивчати твори Б. Кавальєрі, Ж. Роберваля, Б. Паскаля, Р. Декарта, Д. Грегорі і
самого Х. Гюйгенса. Одержимий отриманими знаннями Г. Лейбніц зрозумів, що в
галузі нового аналізу накопичилась значна кількість розв’язань частинних задач
і для відкриття загального методу не вистачає зручної символіки. З 1673 р.
думки з цього приводу не покидали Лейбніца [6].
Зазвичай Лейбніц позначав датою свої
чорнові записи, а тому в загальних рисах можна встановити послідовність і
часові межі створення ним нового числення.
. Знаходження сум рядів і
застосування для цього скінченних різниць (з 1673).
. Розв’язування задач на
дотичні, узагальнення характеристичного трикутника Паскаля, поступовий перенос
співвідношень між скінченними елементами на нескінченно малі.
. Обернені задачі на дотичні,
знаходження сум нескінченно малих різниць, відкриття взаємнооберненості
диференціальних та інтегральних задач (1676).
В процесі відшукання
загального розв’язку задачі про дотичні Г. Лейбніц називає приріст абсциси і
ординати “нескінченно малими різницями”, а в 1675 р. вже з’являється знак (d)
нескінченно малого приросту величини, перед якою його поставлено - dx, dy.
Лейбніц розглядав геометричний зміст похідної: знаходив кутовий коефіцієнт
дотичної до графіка функції. Він користувався не похідною, а диференціалом і
відношенням диференціалів. Тут d - перша буква латинського слова differentia -
різниця, бо ж приріст аргументу і приріст функції - різниця їх значень. Звідси
і пішла назва “диференціальне числення”. Поняття диференціала і символи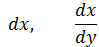 
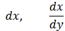широко використовуються в сучасній
математиці.
Першу друковану роботу, в
якій викладались основні поняття і методи диференціального числення, Лейбніц
опублікував у травні 1684 року. Це - мемуар “Новий метод максимумів і
мінімумів, а також дотичних, для якого не є перепоною дробові та ірраціональні
кількості і особливий для цього рід числення”, що з’явився у заснованому ним у
1682 році математичному журналі “Acta Eruditorum”.
За короткими теоретичними
відомостями наводились конкретні приклади застосування викладеного методу:
диференціювання досить складної неявної функції, дослідження шляху, яким
промінь світла за найменший час пройде через два різних середовища;
розв’язування диференціального рівняння [7].
Через два роки, в 1686-му р.,
вийшов у світ мемуари Лейбніца “Про приховану геометрію і аналіз неподільних і
нескінченних величин”, присвячений інтегральному численню. В цьому творі
подавалися прийоми і правила інтегрування багатьох елементарних функцій.
Інтеграл він визначав як суму диференціалів, підкреслюючи взаємну оберненість
операцій інтегрування та диференціювання. Звідси випливали властивості
інтегралів і способи їх обчислення.
В наступних статтях Лейбніц
розвив новий аналіз. Він довів, що будь-яка інтегровна функція є обмеженою, а
також розробив правило обчислення деяких типів інтегралів, зокрема спосіб
інтегрування раціональних функцій.
Основне значення розробленого
Лейбніцом апарата полягало в тому, що завдяки чіткості формулювання і зручності
символіки він став основою нового числення, за допомогою якого виникла
можливість виконувати різноманітні інфінітезимальні дослідження таким самим
способом, як дослідження аналізу скінченних величин за допомогою буквеного
числення [2].
У 90-ті роки до розробки
математичного аналізу приєдналися два видатні швейцарські математики - брати
Яков Бернуллі і Йоганн Бернуллі. Ознайомившись зі статтею Лейбніца, вони не
відразу змогли осягнути її смисл і написали її автору листа з проханням дати
деякі пояснення. Але Лейбніц у цей час подорожував, а тому відповів на листа
лише у 1690 р. На цей час брати не лише розібралися в статті, але й одержали
нові вагомі результати. І. Лейбніц писав братам, що він вважає їх авторами
диференціального числення не менше, ніж самого себе.
У 1696 році з’явився перший
підручник з аналізу. Його написав маркіз Г. Лопіталь під назвою “Аналіз
нескінченно малих для позначення кривих ліній”. Книжка складається з передмови
та 10 глав. У передмові подавався короткий історичний огляд розвитку нового
числення.
В 10 главах книги
викладаються означення сталих і змінних величин та диференціала, виводяться
правила диференціювання алгебраїчних виразів, демонструється застосування
диференціального числення для знаходження дотичних до кривих, для знаходження
максимумів і мінімумів, точок перетину тощо.
Книга Лопіталя добре написана
і містила багато прикладів. Саме з появою цього підручника розпочалося широке
знайомство з аналізом нескінченно малих і поступове проникнення його в
математичну практику.
В основу своєї книги Лопіталь
поклав лекції Й. Бернуллі і те, що він здобув із праць та листів Й. Бернуллі і
Г. Лейбніца. Самостійним у книзі є лише окремі приклади і деяка частина книги,
що стосується дослідження особливих точок кривих. Але з точки зору
впорядкування і розміщення матеріалу, доступності та систематичності
викладення, книга Г. Лопіталя досить оригінальна і цінувалася вище, ніж курс Й.
Бернуллі [11].
На кінець 17 ст. аналіз
нескінченно малих вийшов із стадії формування і постав перед математиками в
образі нової математичної науки. Числення нескінченно малих розширювалося за
рахунок застосувань, однак основні його поняття все ще не були визначені.
Математики 18 ст. розширили
методи математичного аналізу і застосували їх до все складніших функцій. В цей
час аналіз розвивався переважно у трьох напрямах: диференціальне числення,
інтегральне числення та диференціальні рівняння.
Диференціальне числення 18
ст. розвивалося на основі розкладу функцій у степеневі ряди. Методи розроблені
попередниками в 1712 - 1715 рр. поповнилися теоремою Тейлора про розклад
функції у степеневий ряд. Після цього систематичне застосування рядів Тейлора і
Маклорена стало характерною особливістю диференціального числення. Але майже
відразу виникла проблема збіжності рядів, яка супроводжувала розвиток
диференціального числення протягом усього століття. Основні досягнення у
подоланні цієї проблеми стосувалися виведення і дослідження різних форм залишкового
члена ряду, перетворення рядів для отримання завідома збіжних, оперування з
розбіжними рядами [2].
Інтегральне числення 18 ст.
розвивалося як метод знаходження співвідношень між функціями за заданими
співвідношеннями між їх диференціалами. Ідея невизначеного інтегрування на цей
час набула домінуючого значення. Основною метою числення стало формування
методів знаходження первісних для функцій якомога ширшого класу. Інтегральне
числення швидко розросталося і згодом, окрім інтегрування функцій, включало
розв’язування диференціальних рівнянь, варіаційне числення, теорію спеціальних
функцій тощо. Ці галузі математичного аналізу поступово відокремлювалися від
нього протягом 18 ст.
Найбільший внесок у розвиток
і популяризацію диференціального й інтегрального числення у 18 ст. зробив
Леонард Ейлер. Він написав повний курс математичного аналізу. У І. Ньютона, Г.
Лейбніца і у Й. Бернуллі диференціальне числення не виступало у самостійній
формі. У першого воно тісно пов’язане з часом, а через нього - з механікою, у
другого - з геометрією. Ейлер був першим, хто виклав диференціальне числення у
чистому вигляді, як універсальний, ні до чого спеціально не прив’язаний і ні до
чого спеціально не пристосований алгоритм.
Інша велика і багата за
змістом Л. Ейлера - “Диференціальне числення”, яка, крім усього іншого, містила
також і теорію диференціальних рівнянь, теорему Тейлора з багатьма
застосуваннями, формулу знаходження сум Ейлера, ейлерові інтеграли. Головну
увагу в “Диференціальному численні” Ейлер приділяє поняттю похідної, з якої
надалі виходили О. Коші та інші математики першої половини 19 ст. Стверджуючи,
що нескінченно мала величина є нулем, Ейлер будував своєрідне “числення нулів”.
Він вважав, що різниця двох нескінченно малих завжди дорівнює нулю, а відношення
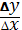
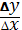може приймати будь-які значення,
одне з яких при наближенні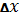 
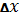до нуля приводить до похідної. Як
бачимо, ейлерове вчення про нескінченно малі в розумінні логістичної
бездоганності не пішло далеко від вчення Лейбніца. Але в книжках Ейлера
спостерігається строга система викладення, виведення нових формул, прикладів і
багато конкретного матеріалу.
Більша частина тому “Диференціальне
числення” присвячена теорії рядів і диференціальним рівнянням. Й цій праці він
увів позначення, які і досі застосовуються (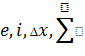
, 
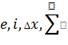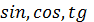
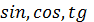та ін.). Для того щоб відрізняти
частинні похідні від звичайних, Ейлер заключав звичайні символи в дужки: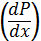 
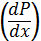і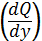 
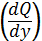. Позначення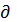 
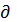увів Г. Якобі (1841) [2].
Книга “Інтегральне числення”
Ейлера представляє собою інтегральне числення як його розуміють тепер, і
зведення знань з інтегрування диференціальних рівнянь. Вона містить, крім
різних методів обчислення інтегралів функцій, вчення про інтегрування звичайних
диференціальних рівнянь.
На відміну від Г. Лейбніца у
Л. Ейлера, як і у І. Ньютона, вихідним було поняття первісної, тобто
невизначеного інтегралу. Визначений інтеграл був для Л. Ейлера частинним
випадком невизначеного, однією з первісних.
Видатних результатів у галузі
математичного аналізу досяг так видатний математики 18 ст. - Ж. Лагранж.
Важливим внеском в загальну теорію стало його узагальнення на функції багатьох
змінних ряду Тейлора, яке було подано в роботі “Про новий ряд числення” (1772
р.).
Класичною стала праця
Лагранжа “Аналітична механіка” (1788), побудована методами математичного
аналізу і викладена як дедуктивна наука. В цій книзі Лагранж робить великий
крок вперед, застосувавши аналіз до теорії ймовірностей.
В “Теорії аналітичних
функцій” (1797) він вивів відповідну формулу Тейлора із залишковим членом. Саме
Лагранжем було введено поняття похідної (1798), до цього користувалися
рівносильним йому поняттям диференціального коефіцієнта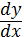 
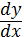. Також йому належить формула
кінцевих приростів, теорія умовних екстремумів. Базуючись на результатах,
отриманих Ейлером, він вперше системно виклав основні поняття варіаційного
числення, яке завдяки йому стало самостійною гілкою математичного аналізу.
У працях “Теорія аналітичних
функцій” і “Лекції про числення функцій” (1801) Лагранж зробив спробу суто
алгебраїчно обґрунтувати диференціальне числення на основі поняття функції і
ряду, звільнивши його від туманних на той час понять нескінченно малої і
границі. Ж. Лагранжу зробити це не вдалося, його нове числення виявилося
складнішим звичайного диференціального числення. Але він зробив надзвичайну і
для свого часу задовільну спробу. Важливість цих праць була в тому, що вони
дали поштовх О. Коші та іншим вченим для пошуку строгої побудови аналізу [13].
Таким чином, у 18 ст.
розширення предмету досліджень математичного аналізу та його застосувань
відбувалося успішно і досить швидкими темпами. Інакше розвивалися події
стосовно обґрунтування нового числення. Понятійний апарат не мав строгих
означень і тлумачень, строгості доведень не приділялась потрібна увага, легко
здійснювався перехід від скінченного до нескінченного, з нескінченостями
оперували як з числами без необхідних на те підстав. Основне поняття, на якому
ґрунтувався весь математичний аналіз, - поняття нескінченно малої величини -
стало його найуразливішим місцем. Але робота з обґрунтування диференціального
та інтегрального числення проведена Л. Ейлером, Ж. Д’Аламбером, Ж. Лагранжем,
Л. Карно та іншими не дала потрібних результатів.
На початку 19 ст. значна
кількість математиків дотримувалась думки, що основою математичного аналізу і
його докорінної перебудови може стати теорія границь. Походження цього поняття
пов’язане з використанням площ криволінійних фігур і об’ємів тіл, що обмежені
кривими поверхнями. Перше теоретичне узагальнення і обґрунтування методів
обчислення площ і об’ємів, в яких неявно використовувалися граничеі переходи
було дано видатним грецьким математиком 4 ст. до н. е. Евдоксом Кнідським.
Методо Евдокса було названо в 17 ст. методом вичерпування. В довгій еволюції
поняття границі (протягом майже 2500 років) метод вичерпування є першим етапом.
Подальший розвиток методу границь відбувався одночасно з розвитком методу
неподільних. Його використовували в своїх дослідженнях і вдосконалювали Б.
Кавальєрі, А. Такке, Д. Валліс, І. Ньютон, Л. Ейлер та інші математики.
Найбільші результати у
перебудові математичного аналізу на основі теорії границь першим отримав О.
Коші. Він виступав як новатор в аналізі і, переглянувши основи диференціального
і інтегрального числення, побудував свій курс аналізу на більш строгих логічних
засадах. Роботи О. Коші з математичного аналізу ґрунтуються на систематичному
використання поняття границі, похідної неперервної функції та їх основних
властивостей. У своїх лекціях з математичного аналізу, що були прочитані в
Політехнічній школі Парижу, а потім викладені у книгах “Курс аналізу” (1821),
“Резюме лекцій із числення нескінченно малих” (1823), “Лекції із застосувань
аналізу до геометрії” (1826-1828), О. Коші побудував увесь математичний аналіз
на основі поняття границі.
В роботі “Курс аналізу”
розглядаються елементарні функції дійсної і комплексної змінної, вчення про
нескінченні ряди, операції диференціювання та інтегрування, поняття границі та
неперервності тощо.
Робота “Резюме лекцій із
числення нескінченно малих” присвячена диференціальному та інтегральному
численню функцій дійсної змінної. В ній Коші відмовляється від розкладання
функцій у нескінченні ряди в усіх випадках, коли тримані ряди не збігаються.
Він наголошує, що використання нескінченно малих кількостей спрощує
диференціальне числення і допомагає викласти його принципи і найважливіші
застосування без допомоги рядів [13].
Інтегральне числення Коші
суттєво відрізнялося від курсу Ейлера та інших попередників. В його основу
покладено поняття визначеного інтегралу, як границі інтегральної суми.
Визначений інтеграл О. Коші розглядав як одне з найважливіших понять аналізу і
позначав його символом 
, що був запропонований Фур’є. Саме
завдяки О. Коші цей символ увійшов у всезагальне використання і зберігся досі.
Автор не просто вводив і використовував це поняття, а й на самому початку лекцій
подавав аналітичне доведення існування визначеного інтеграла від неперервної
функції.
Теоретичне обґрунтування
математичного аналізу О. Коші отримало схвалення науковців і зберігало своє
значення до кінця 19 ст. Але і воно ще не було повністю позбавлене недоліків.
Багато означень у О. Коші носили описовий характер.
Сучасне означення границі,
звільнене від математично незрозумілих термінів, сформував К. Вейєрштрасс. Він
повністю арифметизував означення границі і неперервності. Міра близькості
аргументів і значень функції у нього виражалася нерівностями, що містили
спеціальну символіку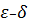 
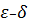. Означеннями К. Вейєрштрасса,
сформульованими на мові 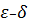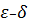, ми користуємося і зараз.
Побудована ним теорія дійсних чисел, у якій дійсні числа розглядаються як
нескінченні десяткові дроби, стала основою системи логічного обґрунтування
математичного аналізу.
У галузі математичного
аналізу слід відзначити ще й такі результати вченого: систематичне використання
верхньої та нижньої меж числових множин, вчення про граничні точки; строге
обґрунтування властивостей неперервних функцій; побудова прикладу неперервної
функції, яка ніде не має похідної; доведення теореми про можливість розкладання
будь-якої неперервної на відрізку функції у рівномірно збіжний ряд многочленів
тощо.
Деякі важливі результати в
галузі обґрунтування аналізу ще до О. Коші і К. Вейєрштрасса одержав професор
філософії релігії Празького університету Б. Больцано. Його математичні
досягнення довгий час не були відомі широкому загалу. Це сталося через те, що
виступаючи за звільнення своєї Батьківщини (Чехії) від австрійської монархії,
Больцано потрапив під таємний нагляд поліції. Його позбавили права публічно
виступати і друкуватися, а згодом звільнили з університету. Лише п’ять робіт з
математики побачили світ за його життя, а решта публікувалися через 100 років.
Зараз історична справедливість відновлена і деякі теореми математичного аналізу
носять подвійне ім’я: теорема Больцано-Коші і теорема Больцано-Вейєрштрасса
[2].
Побудова математичного
аналізу на основі арифметики вимагала строгої теорії дійсного числа, що і було
зроблено майже одночасно Р. Дедекіндом, К. Вейєрштрассом і Г. Кантором.
Великий внесок у розвиток
математичного аналізу 19 ст. М.В. Остроградський. Йому належать найважливіші
результати в галузі інтегрального числення функції багатьох змінних: формула,
що зводить обчислення потрійного ( і взагалі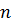 
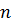-кратного) інтегралу до обчислення
подвійного (
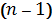
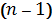-кратного) інтегралу, загальний
прийом інтегрування раціональних функцій, формула перетворення змінних в
багатомірних інтегралах і т.ін.
Кінець 19-го початок 20-го
століття знаменує завершення формування класичного математичного аналізу і
виникнення на його основі різних математичних галузей:
1) Теорія міри та інтеграла.
) Диференціальні рівняння.
) Інтегральні рівняння.
) Комплексний аналіз (теорія
функції комплексної змінної).
) Теорія функції дійсної
змінної.
Як бачимо, математичний аналіз
пройшов довгий шлях свого формування і на сьогоднішній день є однією з основних
галузей математичних наук.
.2 Математичний аналіз як навчальний
предмет
Математичний аналіз -
сукупність розділів математики
<#"815004.files/image017.gif">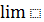
. Велику роль у створенні і розвитку
теорії границь зіграли Л. Ейлер, Б. Больцано та інші. І тільки в руках
французького математика О. Коші (1789-1857) теорія границь стала дійовим
знаряддям для строгого обґрунтування і логічної побудови всього математичного
аналізу. Позиція Коші розвіяла містичний туман, яким до нього були покриті
початки аналізу, і отримала загальне визнання. Варто продемонструвати портрет
Коші, відмітити, що Коші належить до “чистих” математиків 19 ст., оскільки він
надавав великого значення не тільки гнучкості, але й точності як форм, так і
висновків. Роботи Коші, які були присвячені різним галузям математики,
відзначилися сучасною строгістю, обґрунтованістю викладок. Математичні журнали
Франції епохи Коші не встигали друкувати його праці [16].
Що стосується вивчення
неперервності функції однієї змінної, то чотири основні теореми цієї теми
“іменні” (дві теореми Больцано-Коші, дві теореми Вейєрштрасса). Тому бажано
показати портрети Больцано і Вейєрштрасса, відмітивши їх великий внесок у
розвиток математики в цілому. Крім того, можна зауважити, що для окремого
випадку (коли розглядувана функція є цілим многочленом) теореми Больцано-Коші
були сформульовані, без достатнього обґрунтування у роботах Л. Ейлера і Ж.
Лагранжа. Відповідну строгість доведення теорем про властивості неперервних
функцій отримали лише на основі розвинених у другій половині 19 ст.
арифметичних теорій дійсних чисел.
Під час вивчення основ
диференціального та інтегрального числення треба звернути увагу студентів на
те, що ідеї цього числення зародилися ще в 17 ст. Основоположниками
диференціального та інтегрального числення були англійський фізик, астроном і математик
Ісаак Ньютон (1642-1727) та німецький філософ і математик Готфрід Лейбніц
(1646-1716). Перший з них виходив з механічних ідей (задача про швидкість), а
другий - із геометричних (задача про дотичну). Після формулювання означення
похідної функції в точці варто відмітити, що самий термін “похідна” був
введений Ж. Лагранжем на межі 18-го і 19-го століття. І. Ньютон користувався
терміном флексія [20].
Для актуалізації опорних
знань студентів доцільно продемонструвати їм портрети цих вчених і з’ясувати,
які відомості про життєвий і творчий шлях І. Ньютона і Г. Лейбніца студенти
отримали в школі. Для підвищення інтересу студентів до теми і систематизації
отриманих знань бажано показати різні символи, які використовувалися для
позначення похідної:
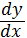
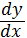або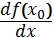 
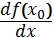(Г. Лейбніц);
ẏ (похідна часу) (І.
Ньютон);
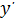
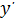або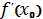 
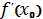(Ж. Лагранж);
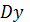
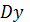або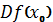 
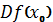(О. Коші).
Після введення означення
диференціала функції варто зауважити, що поняття диференціала і самий термін
“диференціал” (від латинського слова differentia, що означає різниця) належить
Г. Лейбніцу, який точного означення цьому поняттю не дав. Поряд з
диференціалами Г. Лейбніц розглядав частки двох диференціалів, що рівносильно
зараз сучасному позначенню похідних 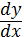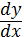. Саме диференціал був для Г.
Лейбніца основним поняттям. І тільки з часів О. Коші, який своєю теорією
границь створив фундамент для аналізу і вперше чітко визначив похідну як
границю, стало звичним спочатку розглядати похідну, а поняття диференціала
будувати вже на основі похідної [14].
Всі теореми теми “Теореми про
середнє значення ” - “іменні”. Тому бажано на лекції дати студентам таке
домашнє завдання: підготувати коротку біографічну довідку про П’єра Ферма,
Мішеля Ролля і Жозефа-Луї Лагранжа. На практичному занятті під час
розв’язування задач на застосування відповідних теорем можна обговорити
відомості, підготовлені студентами.
Матеріал з історії розвитку
математики допоможе викладачам в процесі навчання математичного аналізу
виховувати у студентів патріотизм і гордість за свою Батьківщину. Наприклад,
програма курсу математичного аналізу передбачає в розділі “Невизначений
інтеграл” вивчення теми “Інтегрування раціональних функцій”. В процесі вивчення
цієї теми студенти знайомляться з методом М. В. Остроградського, за допомогою
якого, не виконуючи попередньо інтегрування і, не розкладаючи знаменник на
множники, можна виділити раціональну частину інтеграла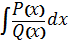 
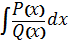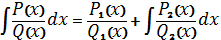
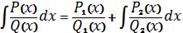. А саме 
, де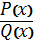 
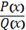- правильний дріб,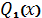 
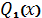- найбільший спільний дільник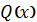 
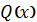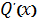
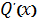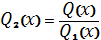
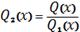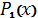
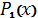і 
, 
, 
і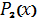 
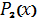- многочлени степеня відповідно на
одиницю менше, ніж степені многочленів 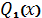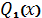і 
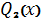
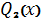[14].
Їх можна знайти методом
невизначених коефіцієнтів з тотожності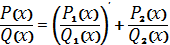 
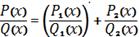. Ця формула дає змогу виділити
раціональну частину інтеграла не виконуючи інтегрування і не розкладаючи
знаменники на множники.
Пояснюючи студентам цей
метод, викладач має чудову нагоду зробити короткий історичний екскурс, скажімо,
так:
- Михайло Васильович
Остроградський (1801-1862) - славетний український математик і механік,
видатний вчений, організатор наукової школи прикладної математики і механіки,
талановитий педагог і прогресивний реформатор математичної освіти.
Багато теорем і формул
Остроградського увійшли в різні математичні курси. Добре відомі математикам
усього світу метод інтегрування Остроградського, правила Остроградського,
формула Остроградського і таке ін. На жаль, його ім’я не завжди згадується.
Через непорозуміння досі говорять про теорему Ліувілля, метод Карно, принцип
Рімана, хоч пріоритет у цих і багатьох інших питаннях належить саме М.
Остроградському. Видатні заслуги М. В. Остроградського визнані усім науковим світом.
Його обрали академіком Російської, Туринської, Римської, Американської
академій, членом-кореспондентом Паризької академії наук та ін.
Вивчення розділу “Кратні інтеграли ”
може завершитися зауваженням такого характеру. Поняття подвійного інтеграла
встановив у 1769 році Л. Ейлер і на різних прикладах показав, як його
обчислювати і застосовувати. Слідом за ним Ж. Лагранж прийшов до потрійних
інтегралів (1773 р.) і розглянув для них питання про перетворення змінних. У
1836 році М.В. Остроградський у повідомленні Петербурзькій академії наук на
тему “Про перетворення змінних у кратних інтегралах” встановив неправильність
міркувань Ж. Лагранжа і дав оригінальне тлумачення цього питання.
Після доведення формули
Остроградського (розділ “Поверхневі інтеграли”) варто зробити застереження:
інколи формулу Остроградського пов’язують з іменем Гаусса. Насправді ж у Гаусса
зустрічаються тільки окремі випадки цієї формули, причому кожен раз заново
дається їх виведення. У загальній формі ця формула була вперше подана у 1828
році М. Остроградським, який застосував її до питання про поширення тепла у
твердому тілі [11].
Після вивчення даного розділу варто
запропонувати студентам самостійно ознайомитись із життєвим шляхом цих видатних
науковців, підготувати про кожного з них короткі біографічні відомості.
В процесі вивчення розділу
“Елементи функціонального аналізу” студенти ознайомлюються з теоремою Банаха та
її застосуванням. Варто повідомити, що ця теорема
<#"815004.files/image039.gif">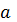
і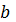 
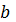цілих і додатних сума всіх дробів
виду 
має границею
одиницю.
В к а з і в к а. Надавати 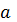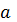і 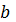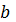різних значень, починаючи з
одиниці; таким чином, весь ряд буде складатися з нескінченної множини спадних
геометричних прогресій.
Дана задача дасть змогу
студентам більш змістовно усвідомити поняття числової послідовності, способи її
задання, деякі види числових послідовностей, границю числової послідовності.
Під час вивчення змістового
модулю “Вступ до аналізу” студентам можна запропонувати такі історичні задачі:
Задача А. Колмогорова
Яку додаткову умову необхідно
накласти на значення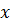 
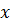у формулі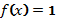 
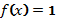, щоб отримати означення функції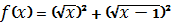 
?
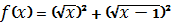В і д п о в і д ь.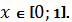 
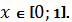
Розв’язуючи дану задачу,
студенти мають змогу закріпити свої знання з таких питань як поняття функції
(поняття відповідності, взаємно однозначної відповідності, функціональної
відповідності) та області її визначення.
Задача Й. Бернуллі
Д о в е д е н н я. 
(сам
Бернуллі замість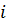 
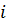писав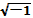 
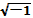). Первісна лівої частини дорівнює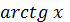 
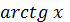, а правої - різниця логарифмів.
Дана задача дасть змогу
студентам більш змістовно усвідомити поняття тригонометричних функцій,
арифметичних дій над цими функціями.
В процесі вивчення змістового
модулю “Інтегральне числення функцій однієї змінної” студентам можна
запропонувати такі історичні задачі:
Задача Е. Торічеллі і Ж.
Роберваля
Показати, що площа арки
циклоїди дорівнює потроєній площі круга, що її утворює.
В к а з і в к а. Скористатися
формулою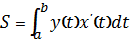 
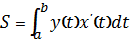і рівнянням циклоїди 
.
Задача Паскаля.
Знайти об’єм тіла, утвореного
обертанням арки циклоїди навколо осі абсцис.
В к а з і в к а. Скористатися
формулою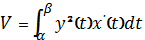 
.
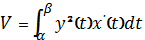Задача Е. Торрічеллі
Довести, що площа
криволінійної трапеції, обмеженої графіком показникової функції, пропорційна
різниці значень цієї функції на кінцях відрізка.
Д о в е д е н н я.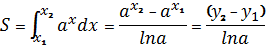 
.
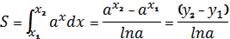Задача У. Нейля.
Обчислити довжину дуги
напівкубічної параболи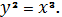 
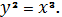
В к а з і в к а. Скористатися
формулою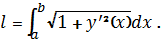 
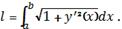
Ці задачі дадуть змогу студентам
більш ґрунтовно усвідомити поняття визначеного інтегралу та його застосування.
Під час вивчення змістового модулю “Числові
ряди” можна розв’язати такі історичні задачі:
Задача Х. Гюйгенса
Знайти суму рядів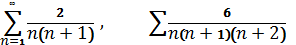 
.
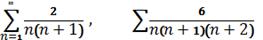В к а з і в к а. Скористатися
тим, що 
означенням
суми ряду.
Задача Я. Бернуллі
Довести, що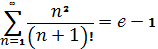 
.
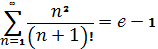Д о в е д е н н я.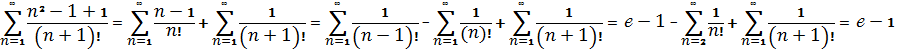 
Оскільки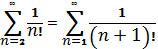 
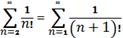, а ряд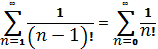 
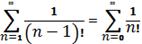отримуємо із ряду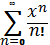 
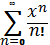, при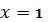 
.
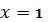Дані задачі дадуть змогу
студентам більш змістовно усвідомити поняття числового ряду і його суми, деяких
числових рядів, необхідної умови збіжності числового ряду, властивості збіжних
числових рядів.
Всі ці історичні задачі були
створені науковцями в різні історичні часи. На той час вони вважалися складними
задачами, і невелика кількість людей, які мали певні теоретичні знання, могли
їх розв’язати. На сьогоднішній день математичний аналіз дуже розвинувся і вже
давно сформований як окремий навчальний предмет, тому теоретичних знань для
розв’язання даних задач в повній мірі вистачає. Звичайно, в процесі вивчення
навчального предмету ці задачі пропонуються для розв’язання як “задачі із зірочкою”,
але кожен студент, в принципі, повинен вміти їх розв’язувати.
.3 Види історичних екскурсів
та їх місце на лекціях
Історичні екскурси, як одна
із складових застосування історизмів, є невід’ємним компонентом в процесі
вивчення математичного аналізу. Особливо це стосується лекційного матеріалу з
даного навчального предмету, оскільки в процесі лекцій студенти постійно
знайомляться з новими іменами творців даної математичної галузі, певними
“іменними” теоремами, аксіомами, правилами, алгоритмами, поняттями і т.д.
У процесі вивчення
математичного аналізу варто використовувати такі види історичних екскурсів:
· Історичні відступи
на лекціях чи практичних заняттях;
· Повідомлення
історичних відомостей, органічно пов’язаних з теорією і задачами;
· Реферати чи короткі
доповіді студентів;
· Історичні
повідомлення, що супроводжуються комп’ютерною презентацією, які включають такий
матеріал, як біографії вчених та їх портрети, походження математичних термінів,
легенди та ін.
Далі розглянемо, які із поданих
видів варто використовувати на кожній із лекцій.
Вивчаючи розділ “Дійсні числа”, а
саме - питання “Множина ірраціональних чисел”, доцільно зауважити, що вперше
ірраціональні числа з’явилися ще в середні віки (у вигляді виразів, що містять
радикали). У 18 ст. питання про ірраціональні числа розглядалися у зв’язку з
вираженням геометричних величин. Критичний напрямок у математиці, який виник у
кінці 18 ст. - на початку 19 ст., висунув вимогу точного означення основних
понять аналізу і строгого доведення його основних положень [19]. Це, в свою
чергу, зробило необхідним побудову логічно досконалої теорії ірраціональних, а
потім і дійсних чисел на основі чисто арифметичного їх означення. У кінці 19
ст. було створено кілька таких теорій, різних за формою, але по суті рівносильних.
Основні з них:
· Теорія Гільберта
(аксіоматична теорія);
· Теорія Вейєрштрасса
(ґрунтується на десятковому зображенні дійсного числа);
· Теорія Дедекінда
(на основі перерізів);
· Теорія Кантора (за
допомогою фундаментальних послідовностей).
Предметом математичного аналізу є
функція. Тому після ознайомлення студентів з поняттям функції, з основними
способами задання функції, варто коротко зупинитися на генезисі цього поняття.
Виникненню поняття функції
передувало введення в математику змінної величини, яке зазвичай пов’язують з
іменем французького математика Р. Декарта (1596-1650). Самий термін функція
з’явився у роботі Г. Лейбніца у 1692 році і використовувався для характеристики
різних відрізків, пов’язаних з точками деякої кривої. Перше означення функції,
яке вже не було пов’язане з геометричними уявленнями, дав Й. Бернуллі у 1718
році. Л. Ейлер (1707-1783) у 1748 році дав означення функції, за яким вона
ототожнювалася з тим аналітичним виразом, яким вона була задана. Він же ввів
звичне для нас позначення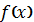 
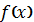. М. Лобачевський у 1834 році, а П.
Діріхле у 1837 році, означаючи поняття функції, на перший план висувають ідею
відповідності між елементами двох числових множин. В процесі лекції варто
показати студентам портрети даних вчених і запропонувати їм підготувати короткі
історичні доповіді про цих науковців, з яким вони можуть виступити на
практичних заняттях [20].
Вивчаючи тему “Диференціал
функції”, варто подати такі історичні відомості. В математичному аналізі
<#"815004.files/image012.gif">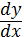, що також може бути записано
(позначення Ньютона чи Лагранжа)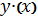 
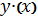чи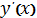 
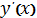. Використання диференціалів в такій
формі спровокувало багато критики, наприклад знаменитий памфлет The Analyst
єпископа Берклі [20]. В будь-якому разі таке позначення залишилось популярним,
тому що воно наочно відображає принцип, що похідна функції y(x) дорівнює нахилу
<#"815004.files/image004.gif">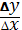 приросту y в залежності від
приросту x, якщо приріст x прямує до нуля. Диференціали також застосовують в
аналізі розмірності, де диференціал наприклад dx має таку саму розмірність як і
змінна x. Диференціал використовують в позначенні інтеграла
<#"815004.files/image073.gif">
, знак інтеграла (витягнуте s)
означає нескінченну суму, f(x) позначає “висоту” тонкої стрічки, а диференціал
dx позначає нескінченно тонку ширину.
Вивчаючи тему “Визначений
інтеграл”, студенти розглядають такі поняття як: інтеграл Рімана, властивості
визначеного інтегралу, головна теорема інтегрального числення, узагальнення
визначеного інтеграла. Варто додати, що існує кілька різновидів визначених
інтегралів: інтеграл Лебега
<#"815004.files/image074.gif">
: якщо фукція належить H, то її
модуль також належить H.
Крім того, на просторі
елементарних функцій визначається додатньо визначений неперервний
<#"815004.files/image075.gif">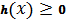
, тоді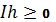 
.
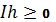. Неперервність: якщо
hn(x) незростаюча послідовність (тобто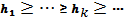
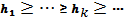) функцій з H, які збігаються до
нуля для всіх x в X, тоді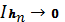 
.
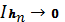У цих термінах можна
визначити множину
<#"815004.files/image079.gif">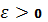
існує неспадна послідовність невід'ємних
елементарних функцій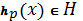 
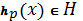така, що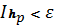 
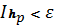і 
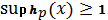
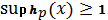на Z.
Якщо деяка умова виконується
на X скрізь, окрім, можливо, підмножини міри нуль, то говорять, що вона
виконується майже всюди
<#"815004.files/image083.gif">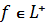
за визначенням дорівнює: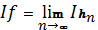 
.
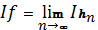Можна показати, що це
визначення коректне, тобто воно не залежить від вибору послідовності {hn}.
За допомогою цієї конструкції
можуть бути доведені майже всі теореми теорії інтеграла Лебега, наприклад
теорема Лебега про домінантну збіжність, теорема Тонеллі - Фубіні, лема Фату
<#"815004.files/image085.gif">,
де N - загальна кількість
студентів експериментальної та контрольної групи,
А і В - кількість студентів
експериментальної і контрольної групи відповідно, які отримали не менше 8
балів,
С і D - кількість студентів
експериментальної і контрольної групи відповідно, які отримали не більше 8
балів. Для 13-М групи (спеціальність математика): A=0, B=11, C=0, D=8. Для 14-Ф
групи (спеціальність фізика): A=15, B=0, C=4, D=0. Тоді Тсп ≈
8,2 для контрольної групи і Тсп ≈ 12,1 для експериментальної
групи.
Порівнюючи отримані значення
Т з відповідним наближеним значенням Ткр ≈ 3,84, приходимо до
висновку, що Тсп > Ткр. А це означає, що медіани
розподілу студентів в експериментальній і контрольній групах відрізняються одна
від одної зі збільшенням в сторону експериментальних.
Це дає підстави говорити про вищий
інтерес студентів експериментальної групи до навчального предмету.
Для визначення ефективності
запропонованої методики проводилися бесіди з викладачами, які брали участь у
формуючому етапі експерименту. Викладачі позитивно оцінили запропоновану
методику, відзначили підвищення рівня інтересу студентів, підвищення
інтелектуального розвитку, покращення якості та успішності навчання.
Отже, педагогічний експеримент
підтвердив гіпотезу нашого дослідження, оскільки його результати свідчать про
підвищення інтересу студентів до вивчення математичного аналізу і, як наслідок,
покращенню рівня знань і якості успішності.
У другому розділі, спираючись на
теоретичні засади викладені в першому розділі, підібрано необхідний історичний
матеріал для проведення запропонованої історичної методики. На основі
проведеного дослідження можна сформулювати такі висновки:
) Ознайомлення студентів з
творцями математичного аналізу є невід’ємною складовою процесу вивчення
лекційного курсу даного предмету, оскільки студенти постійно стикаються з
“іменними” теоремами, аксіомами, означеннями, правилами, алгоритмами і т.д.
) Історичні задачі є одним із
ефективних засобів створення проблемної ситуації на лекціях з математичного
аналізу, тому що в результаті мисленнєвої взаємодії студента з навчальним
матеріалом, виникає пізнавальна потреба розкрити суть процесу або явища, що
вивчається.
) Історичні екскурси, як одна
із складових застосування історизмів, є невід’ємним компонентом в процесі
вивчення математичного аналізу. Викладачеві потрібно підібрати необхідний вид
даного екскурсу, який доцільно використовувати на кожній лекції.
) Експериментальне
дослідження показало, що рівень інтересу студентів до вивчення математичного
аналізу можна підвищити, якщо створити для цього сприятливі умови:
а) забезпечити мотиваційну і
психологічну готовність студентів до використання історичного матеріалу шляхом
його систематичного застосування на лекціях з математичного аналізу;
б) підбирати необхідний вид
історичних екскурсів, який доцільно використовувати на кожній лекції з певної
теми;
в) включати в лекційний курс
математичного аналізу історичні задачі як засіб створення проблемних ситуацій
на лекціях.
лекція математичний
педагогічний історичний
Висновки
Розглянувши математичний аналіз як
науку і навчальний предмет, проаналізувавши стан проблеми дослідження в
університеті, підібравши необхідний історичний матеріал та провівши
експериментальне дослідження, я можу зробити такі висновки:
1. Проблема застосування
історичного матеріалу на лекціях з математичного аналізу є актуальною на
сьогоднішній день, але більшість викладачів-математиків не звертають увагу на
цей факт, а проводять заняття у типовій формі, не застосовуючи історичних задач
або інших історичних повідомлень. Тоді як аналіз проявів інтересу студентів
показав, що більшість із них мають невисокий рівень інтересу до даного
навчального предмету, що в свою чергу впливає на їхній низький рівень знань.
. У науковій літературі
широко висвітлено різні види історичних екскурсів. Дослідження показало, що на
лекціях з математичного аналізу варто використовувати такі види історичних
екскурсів як історичні відступи, повідомлення історичних відомостей, органічно
пов’язаних з теорією та задачами, реферати чи короткі відповіді студентів,
історичні повідомлення, що супроводжуються комп’ютерною презентацією, які
включають такий матеріал, як біографії вчених та їх портрети, походження
математичних термінів, легенд та ін. Експериментальна перевірка показала, що
саме ці види історичних екскурсів органічно вплітаються в лекційний курс
навчального предмету і ефективно впливають на прояви інтересу студентів до
нього.
. Для забезпечення реалізації
мети дипломної роботи до застосування історизмів на лекціях з математичного
аналізу, необхідно проаналізувати і чітко виділити програмові вимоги до
теоретичних знань та практичних умінь студентів по даному навчальному предмету.
Список використаних джерел
. Бевз В.Г. Історія
математики у фаховій підготовці майбутніх вчителів. / В.Г. Бевз - К.: НПУ імені
М.П. Драгоманова, 2005. - 356 с.
. Вивальнюк Л.М. Елементи
історії математики: / Л.М. Вивальнюк, М.Я. Ігнатенко // Навч. посібник. - К.:
ІЗМН, 1996. - 241 с.
. Вилейтнер Г. История
математики от Декарта до середины XIX столетия. / Г. Вилейтнер // - М.: Наука,
1966. - 508 с.
. Грабарь М.И.
Применение математической статистики в педагогических исследованиях: / М.И.
Грабарь, К.А. Краснянская // Непараметрические методы. - М.: Просвещение, 1977.
- 136 с.
. Даан-Дальмедико А.
Пути и лабиринты. Очерки по истории математики. / А. Даан-Дальмедико, Ж. Пейфер
- М.: Мир, 1986. - 287 с.
. Дороговцев А.Я.
Математический аналіз / А.Я. Дороговцев // Справочное пособие. - К.: Вища шк.
Головное изд-во, 1985. - 528 с.
. Конфорович А.Г.
Визначні математичні задачі. / А.Г. Конфорович / - К.: Рад. школа, 1981. - 189
с.
. Конфорович А.Г.
Історія розвитку математики: / А.Г. Конфорович, А.М. Андрієвська // Альбом:
Навчальний наочний посібник. - К.: Вища школа, 1987. - 263 с.
. Клейн Ф. Лекции о
развитии математики в XIX ст. Т.1.: / Ф. Клейн // Пер. с нем. - М.: Наука,
1989. - 273 с.
. Колмогоров А.Н.
Математика в её историческом развитии / А.Н. Колмогоров // Под ред. В.А.
Успенского. - М.: Наука, 1991. - 318 с.
. Назаров В.Ю. Елементи
історії математики: / В.Ю. Назаров // Навч. пос. для студентів ф.-м.
факультетів. - Ніжин: НДПУ, 2002. - 238 с.
. Рыбников К.А. История
математики. / К.А. Рыбников - М., 1974. - 346с.
. Стройк Д.Я. Краткий
очерк по истории математики. / Д.Я. Стройк / - М., 1964. - 273 с.
. Стройк Д.Я. Коротка
історія математики / Д.Я. Стройк // Пер. з англ. і доповнення С.М. Кіро. - К.:
Рад. школа, 1960. - 305 с.
. Тихомиров В.
Математика во второй половине XX века. / В. Тихомиров / Квант. - 1999. - №1. -
284 с.
. Тихомиров В.
Математика в первой половине XX века. / В. Тихомиров / Квант. - 2000. - № 1-2.
- 337 с.
. Фихтенгольц Г.М.
Основы математического анализа. / Г.М. Фихтенгольц / Т. 1. - М., 1956. - 440 с.
. Фрейман Л.С. Творцы
высшей математики. / Л.С. Фрейман / - М.: Наука, 1968. - 289 с.
. Цейтен Г.Г. История
математики в древности и в средние века. / Г.Г. Цейтен - М.: Л., 1948. - 337 с.
. Цейтен Г.Г. История
математики в XVI - XVII вв. / Г.Г. Цейтен / - М.: Л., 1933. - 359 с.
. Чистяков В.Д.
Старинные математические задачи. / В.Д. Чистяков / - Минск, 1966. - 248 с.
. Шереметьевский А.П.
История математики в средние века. / А.П. Шереметьевский / - М., 1961. - 372 с.
. Юшкевич А. . История
математики в Средние века. / А.П. Юшкевич / - М., 1961. - 351 с.
. Юшкевич А.П. История
математики в России до 1917 г. / А.П. Юшкевич / М., 1968. - 349 с.