Решение системы уравнений методом Гаусса
Типовой расчет 1
<#"732219.files/image001.gif">
Решение
А) по формулам Крамера

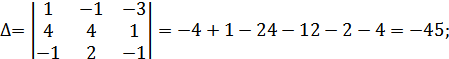
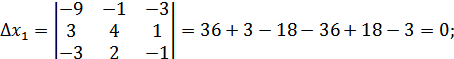

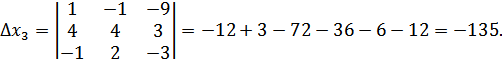
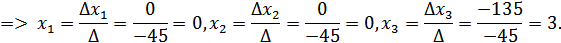
Проверка:
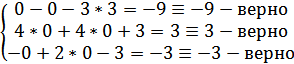
Б) методом Гаусса
Составляем расширенную матрицу системы:

Исходная система после преобразований:
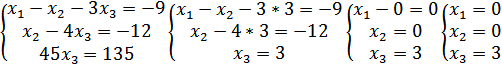
Ответ: 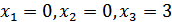 .
.
Задача № 2. Решить систему уравнений (В)
матричным методом.
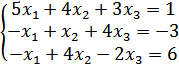
Решение
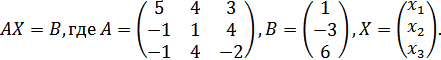
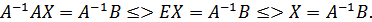
Здесь  -
обратная матрица,
-
обратная матрица,  .
.
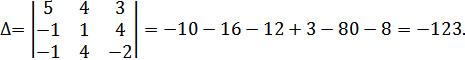
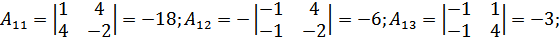


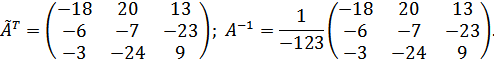
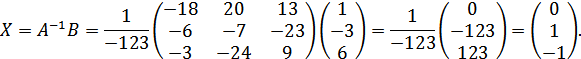
Проверка:
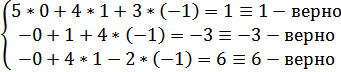
Ответ:  .
.
Задача № 3. Решить систему уравнений (С).

Решение
Приведем систему к ступенчатому виду:


Очевидно, ранг расширенной матрицы равен рангу
основной матрицы системы. Следовательно, по теореме Кронекера-Капелли система
является совместной.
Пусть 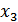 -
свободная переменная,
-
свободная переменная,  Тогда:
Тогда:
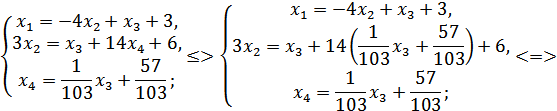
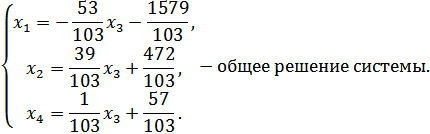
Полагая,  ,
частное решение системы:
,
частное решение системы: 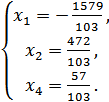
Задача № 4. Даны вершины пирамиды 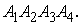
A1(1; -9; 2), A2(-2; -11; 5), A3(4; -12; 3),
A4(-1; -10; 3)
Средствами векторной алгебры найти:
Объем пирамиды;
Площадь грани 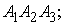
Угол между ребрами 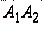 и
и

Величину проекции вектора  на
направление вектора
на
направление вектора 
Решение
Объем пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах 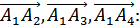
крамер гаусс векторный алгебра

Найдем координаты этих векторов:
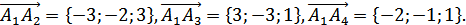
Тогда объем пирамиды:
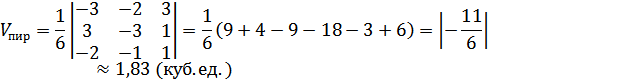
Площадь грани  :
:

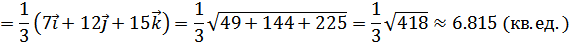
Угол между ребрами  и
и
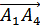 найдем
по следующей формуле:
найдем
по следующей формуле:
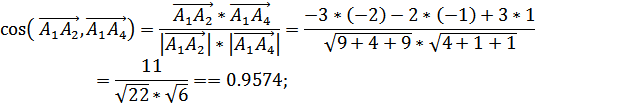

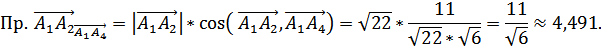
Типовой расчет 2
<#"732219.files/image052.gif">:
А(-7; -2), B(-19; -18), C(5; -11)
Найти:
Уравнение стороны ВС;
Уравнение высоты AD;
Уравнение медианы AM;
Длину высоты AD;
Длину медианы AM.
Решение
Уравнение прямой, проходящей через
точки B и C:
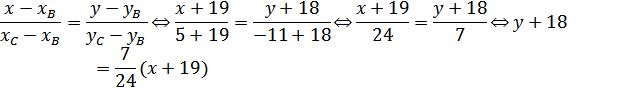
Высота AD, проведенная к стороне BC:

Уравнение стороны BC:  .
.
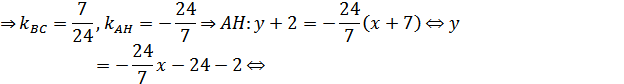
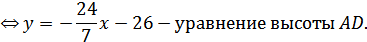
Координаты точки M: 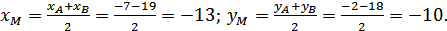
Тогда уравнение медианы AM: 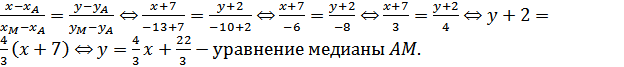
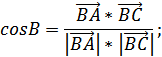
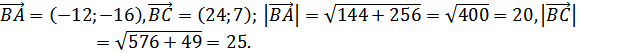
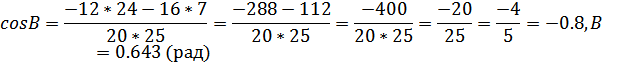
Расстояние от точки A до прямой BC это есть
длина высоты AD:
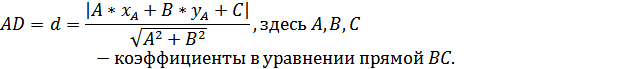
Уравнение прямой BC: 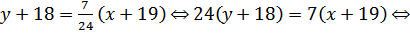

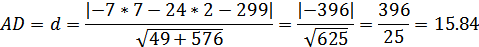
Длина медианы AM: 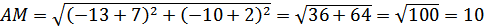
Задача № 2. Составить уравнение плоскости,
проходящей через:
Точки 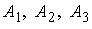 ;
Точку
;
Точку  перпендикулярно
прямой
перпендикулярно
прямой  ;
;
Точку 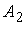 и
прямую
и
прямую 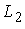 ;
;
Точку 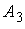 параллельно
плоскости
параллельно
плоскости 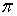 ;
;
Точки  и
и
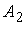 параллельно
оси Ох.
параллельно
оси Ох.
(4; 1; -10), A2(7; 2; -7), A3(5; 3; -9),
A4(2; 2; -13)
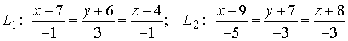
π: 4x + 3y - 2z + 4 = 0
Решение
Уравнение плоскости через 3 точки в общем виде:
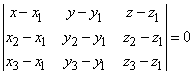
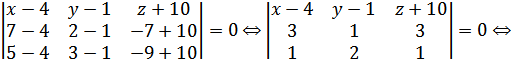
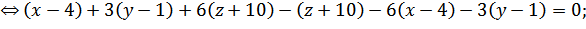

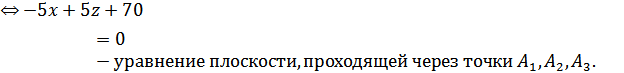
Направляющий вектор прямой L1: s{-1;3;-1}.
Следовательно, для искомой плоскости нормаль будет иметь координаты {-1;3;-1},
так как прямая и плоскость перпендикулярны.
Уравнение плоскости, проходящей через точку
A1(4;1;-10):
(x - 4) + B(y - 1) + C(z + 10) = 0,
где {A;B;C}- координаты вектора нормали к
плоскости {-1;3;-1}. Тогда уравнение искомой плоскости, проходящей через точку
A1 перпендикулярно прямой L1:
(x - 4) - 3(y - 1) + (z + 10) = 0;
x - 3y + z +17 = 0 - уравнение искомой
плоскости.
Плоскость, проходящая через точку М0(х0;у0;z0) и
через прямую K
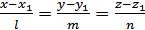 ,
,
не проходящую через М0, представляется
уравнением:
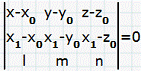
Получим:
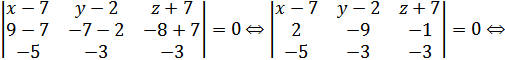
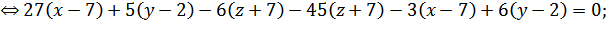
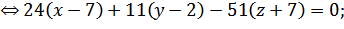
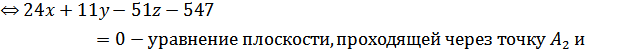
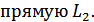
Для двух параллельных плоскостей векторы
нормалей коллинеарны. Поэтому для искомой плоскости вектор нормали совпадает с
вектором нормали заданной плоскости 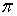 :
{4;3;-2}. Уравнение плоскости, проходящей через точку A3(5; 3; -9) и с вектором
нормали {4;3;-2}:
:
{4;3;-2}. Уравнение плоскости, проходящей через точку A3(5; 3; -9) и с вектором
нормали {4;3;-2}:
(x - 5) + 3(y - 3) - 2(z + 9) = 0;
x + 3y - 2z - 47 = 0 - уравнение прямой,
проходящей через точку A3 параллельно плоскости 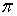 .
.
Уравнение прямой, параллельной оси абсцисс имеет
вид: By + Cz + D = 0 (1).
Если плоскость проходит через точку, то
координаты этой точки удовлетворяют уравнению плоскости. Подставляем координаты
точек A1(4; 1; -10), A2(7; 2; -7) в уравнение плоскости (1) и получаем систему
двух уравнений:

Для определения коэффициентов A, B и D имеем
систему двух однородных линейных уравнений с тремя неизвестными. Составляем
матрицу коэффициентов этих уравнений:

Подставляем найденные значения в уравнение (1):
ty + tz + 27t = 0;
y + z + 27 = 0 - уравнение прямой, проходящей
через точки A1(4; 1; -10), A2(7; 2; -7) параллельно оси Ох.
Задача № 3. Составить канонические уравнения прямой,
проходящей через:
Точку  параллельно
прямой
параллельно
прямой  ;
;
Точки  и
и
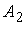 ;
;
Точку  перпендикулярно
плоскости
перпендикулярно
плоскости 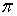 .
.
(4; 1; -10), A2(7; 2; -7), A3(5; 3; -9),
A4(2; 2; -13)
π: 4x + 3y - 2z + 4 = 0

Уравнение прямой, проходящей через точку A1(4;
1; -10):
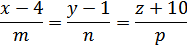
Здесь {m;n;p} - координаты направляющего вектора
прямой.
Так как искомая прямая параллельная прямой L1,
тогда координаты их направляющих векторов пропорциональны. А это значит, что m
= -1, n = 3, p = -1. Тогда искомое уравнение прямой:

Уравнение прямой, проходящей через точки A1(4;
1; -10), A2(7; 2; -7):

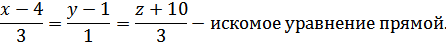
Уравнение прямой, проходящей через данную точку
M(x1,y1,z1) и перпендикулярной данной плоскости Ax+By+Cz+D=0

В нашем случае, уравнение прямой, проходящей
через точку A1(4; 1; -10) перпендикулярно плоскости π:
4x + 3y - 2z + 4 = 0:

Задача № 4. Найти:
Угол между прямыми  и
и
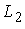 ;
;
Угол между прямой  и
плоскостью
и
плоскостью 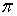 ;
;
Расстояние от точки  до
плоскости
до
плоскости 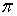 .
.
(4; 1; -10), A2(7; 2; -7), A3(5; 3; -9),
A4(2; 2; -13)
π: 4x + 3y - 2z + 4 = 0
Решение
Воспользуемся формулой:
 .
.
Получим:
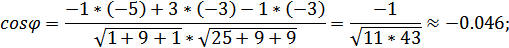

Угол ψ между
прямой K (с направляющими коэффициентами l, m, n) и плоскостью Ах+By+Cz+D=0
находится по формуле:


Расстояние от точки до плоскости в общем виде:
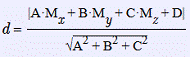
В нашем случае, расстояние от точки A1(4; 1;
-10)до плоскости π: 4x + 3y - 2z + 4 = 0 равно:
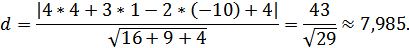
Задача № 5. Привести к каноническому виду
уравнения (1) и (2) кривых второго порядка. Построить кривые.
(1) y2 - 3x - 2y + 7 = 0, (2) x2 + 4y2 + 4x -
8y - 56 = 0
Решение
- 3x - 2y + 7 = 0;
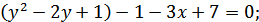
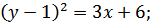
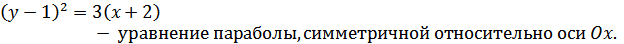
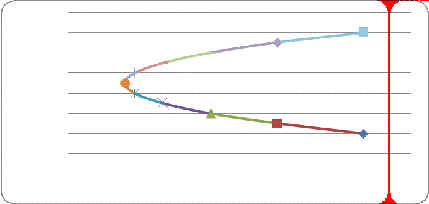
Рис. 1
+ 4y2 + 4x - 8y - 56 = 0;

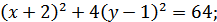

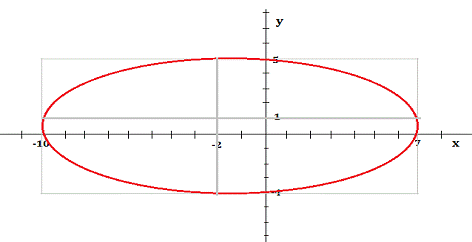
Рис. 2