Численные методы решения трансцендентных уравнений
Аннотация
Основной целью данной курсовой работы является изучение и сравнительный
анализ численных методов решения трансцендентных уравнений.
В данной курсовой работе рассмотрено 5 методов решения трансцендентных
уравнений.
Трансцендентными называются уравнения, не являющиеся алгебраическими.
Т.е. содержащие функции (тригонометрические, показательные, логарифмические и
др.).
Методы решения трансцендентных уравнений делятся на прямые и
итерационные. Прямые методы позволяют записать корни в виде некоторого конечного
соотношения или в виде формулы. Итерационные методы являются приближенными
методами.
Оглавление:
) Введение
2) Общая информация
) Метод половинного деления (Дихотомии)
) Метод простой итерации
) Метод хорд
6) Метод Ньютона (Метод касательных, линеаризации)
7) Метод хорд и касательных
) Заключение
9) Литература
10) Приложение
1. Введение
Трансцендентное
уравнение - уравнение
<#"663909.files/image001.gif">
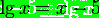
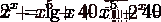
Более
строгое определение таково:
Трансцендентное
уравнение - это уравнение вида  , где
функции
, где
функции 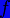 и
и 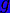 являются
аналитическими функциями
<#"663909.files/image007.gif"> уравнения
х 3 - 3× х +1 = 0 с точностью 10 -3 (табл. 2) .
являются
аналитическими функциями
<#"663909.files/image007.gif"> уравнения
х 3 - 3× х +1 = 0 с точностью 10 -3 (табл. 2) .
Таблица
2
|
N
|
a n
|
b n
|
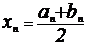 f(x n) f(x n)
|
|
|
0
|
0
|
1
|
0,5
|
-0,375
|
|
1
|
0
|
0,5
|
0,25
|
0,2656
|
|
2
|
0,25
|
0,5
|
0,375
|
-0,0723
|
|
3
|
0,25
|
0,375
|
0,3125
|
0,0930
|
|
4
|
0,3125
|
0,375
|
0,3438
|
0,0092
|
|
5
|
0,3438
|
0,375
|
0,3594
|
-0,0318
|
|
6
|
0,3438
|
0,3594
|
0,3516
|
-0,0113
|
|
7
|
0,3438
|
0,3516
|
0,3477
|
-0,0011
|
|
8
|
0,3438
|
0,3477
|
0,0040
|
|
9
|
0,3458
|
0,3477
|
0,3468
|
0,0013
|
|
10
|
0,3468
|
0,3477
|
0,3473
|
|
|a10 - b10| = |0,3468 - 0,3477| = 0,0009 < 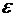 ,
где
,
где
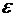 = 0,001.
= 0,001.
x » 0,347 .
4. Метод простой итерации
Или
метод последовательных приближений. Чтобы применить этот метод для решения
уравнения (1) необходимо преобразовать его к виду 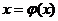 . Далее выбирается начальное приближение
. Далее выбирается начальное приближение 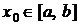 и вычисляется x1, затем x2 и
т.д.:
и вычисляется x1, затем x2 и
т.д.:
x1 = j(x0);
x2 = j(x1);
…;
xk = j(xk-1);
Если
xn стремится к некоторому пределу x, то
этот предел и есть корень уравнения.
Полученная
последовательность сходится к корню при выполнении следующих условий:f
)
функция j(x) дифференцируема на интервале [a, b].
)
во всех точках этого интервала j¢(x) удовлетворяет
неравенству:
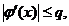 0 £ q £ 1 (2)
0 £ q £ 1 (2)
При
таких условиях скорость сходимости является линейной, а итерации следует
выполнять до тех пор, пока не станет справедливым условие:
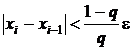 . (3)
. (3)
Критерий
вида
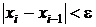 , (4)
, (4)
может
использоваться только при 0 £ q £ ½.
Иначе итерации заканчиваются преждевременно, не обеспечивая заданную точность.
Если вычисление q затруднительно, то можно использовать критерий окончания вида
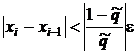 ;
; 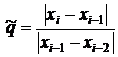 . (5)
. (5)
Возможны
различные способы преобразования уравнения (1) к виду 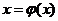 . Следует выбирать такой, который удовлетворяет
условию (4), что порождает сходящийся итерационный процесс, как, например, это
показано на рис. 2, 3. В противном случае, в частности, при ½j¢(x)½>1,
итерационный процесс расходится и не позволяет получить решение (рис. 4).
. Следует выбирать такой, который удовлетворяет
условию (4), что порождает сходящийся итерационный процесс, как, например, это
показано на рис. 2, 3. В противном случае, в частности, при ½j¢(x)½>1,
итерационный процесс расходится и не позволяет получить решение (рис. 4).
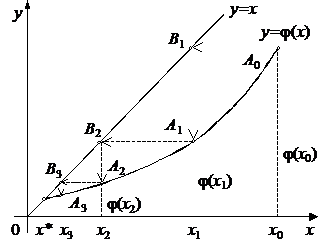
Рис. 2

Рис. 3

Рис.4
Говорят, что итерационный процесс сходится, если при выполнении
последовательных итераций получаются значения корней, все ближе и ближе
приближающиеся к точному значению корня. В противном случае итерационный
процесс считается расходящимся.
Почти все итерационные методы, в том числе и метод простых итераций,
имеют важное достоинство: в них не накапливаются ошибки вычислений. Эта ошибка
эквивалентна некоторому ухудшению следующего приближения. Однако это не
отразится на результате и будет заметно лишь по количеству итераций.
Даже грубые ошибки не могут причинить видимого вреда. Но только если
ошибка не выбрасывает приближение за пределы области сходимости.
Пример. Необходимо методом итераций уточнить корень xÎ[0;1] уравнения: х 3 - 3×х +1 = 0, с точностью 10 -3 (табл.
3).
Преобразованное уравнение:
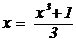 .
.
Таблица
3
|
n
|
х n
|
j (x n)
|
|
0
|
0
|
0,3333
|
|
1
|
0,3333
|
0,3457
|
|
2
|
0,3457
|
0,3471
|
|
3
|
0,3471
|
0,3473
|
|
4
|
0,3473
|
|
êх 4 - х 3 ê < e
x » 0,347.
5. Метод хорд
Или метод пропорциональных частей, хотя я так и не понял почему. Пусть
дано уравнение f(x) = 0, где f(x) - непрерывная функция, имеющая в интервале
(a, b) производные первого и второго порядков. Корень считается отделенным и
находится на отрезке [a, b].
Идея метода хорд состоит в том, что на достаточно малом промежутке [a, b]
дугу кривой y = f(x) можно заменить хордой и в качестве приближенного значения
корня принять точку пересечения с осью абсцисс. Рассмотрим случай, когда первая
и вторая производные имеют одинаковые знаки, т.е. f '(x)f ²(x) > 0. Тогда уравнение хорды, проходящей через точки A0 и B, имеет вид
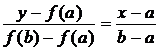 . (6)
. (6)
Приближение
корня x = x1, для которого y = 0, определяется как
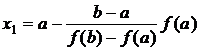 . (7)
. (7)
Аналогично
для хорды, проходящей через точки A1 и B, вычисляется следующее приближение
корня
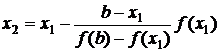 . (8)
. (8)
В
общем случае формула метода хорд имеет вид:
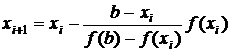 . (9)
. (9)
Если первая и вторая производные имеют разные знаки, т.е.
то все приближения к корню x* выполняются со стороны правой границы
отрезка [a, b], как это показано на рис. 6, и вычисляются по формуле:
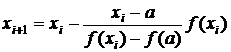 . (10)
. (10)
Выбор
формулы в каждом конкретном случае зависит от вида функции f(x) и
осуществляется по правилу: неподвижной является граница отрезка [a, b] изоляции
корня, для которой знак функции совпадает со знаком второй производной. Формула
(9) используется в том случае, когда f(b)f "(b) > 0. Если справедливо неравенство f(a)f "(a) > 0, то целесообразно применять формулу (10).
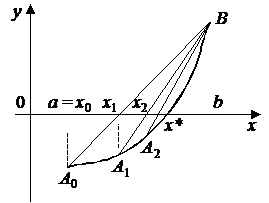

Рис. 5 Рис. 6
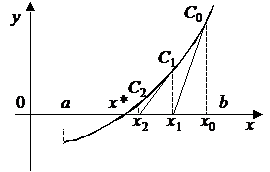
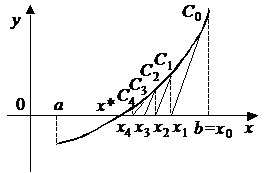
Рис.
7 Рис. 8
Итерационный процесс метода хорд продолжается до тех пор, пока не будет
получен приближенный корень с заданной степенью точности. При оценке
погрешности приближения можно пользоваться соотношением:
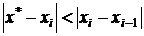 . (11)
. (11)
Тогда
условие завершения вычислений записывается в виде:
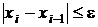 . (12)
. (12)
где
e - заданная погрешность вычислений. Необходимо
отметить, что при отыскании корня метод хорд нередко обеспечивает более быструю
сходимость, чем метод половинного деления.
Пример. Необходимо методом хорд уточнить корень x Î [0;1] уравнения х 3 - 3×х + 1 = 0 с точностью 10 -3 (табл. 4)
.
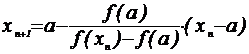 ;
;
а
= 0; f(a) = 1.
Таблица
4
|
n
|
х n
|
x n - a
|
f(x n )
|
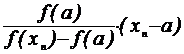
|
|
0
|
1
|
1
|
-1
|
-0,5
|
|
1
|
0,5
|
0,5
|
-0,375
|
-0,3636
|
|
2
|
0,3636
|
0,3636
|
-0,0427
|
-0,3487
|
|
3
|
0,3487
|
0,3487
|
-0,0037
|
-0,3474
|
|
4
|
0,3474
|
0,3474
|
-0,0003
|
-0,3473
|
|
5
|
0,3473
|
|
|
|
½x 5 - x 4½ < e.
x » 0,347.
6. Метод Ньютона (Метод касательных, линеаризации)
Пусть уравнение (1) имеет корень на отрезке [a, b], причем f '(x) и f
"(x) непрерывны и сохраняют постоянные знаки на всем интервале [a, b].
Геометрический смысл метода Ньютона состоит в том, что дуга кривой y =
f(x) заменяется касательной. Для этого выбирается некоторое начальное
приближение корня x0 на интервале [a, b] и проводится касательная в точке
C0(x0, f(x0)) к кривой y = f(x) до пересечения с осью абсцисс. Уравнение
касательной в точке C0 имеет вид
= f(x0) + f '(x0)×(x - x0). (13)
Далее за приближение корня принимается абсцисса x1, для которой y = 0:
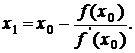 (14)
(14)
Затем
проводится касательная через новую точку C1(x1, f(x1)) и определяется точка x2
ее пересечения с осью 0x и т.д. В общем случае формула метода касательных имеет
вид:
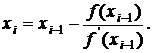 (15)
(15)
В
результате вычислений получается последовательность приближенных значений x1,
x2, ..., xi, ..., каждый последующий член которой ближе к корню
x*, чем предыдущий.
Начальное
приближение x0 должно удовлетворять условию:
(x0)
f ¢¢(x0) > 0. (16)
В
противном случае сходимость метода Ньютона не гарантируется, так как
касательная будет пересекать ось абсцисс в точке, не принадлежащей отрезку [a,
b]. На практике в качестве начального приближения корня x0, обычно выбирается
одна из границ интервала [a, b], т.е. x0 = a или x0 = b, для которой знак
функции совпадает со знаком второй производной.
Метод
Ньютона обеспечивает высокую скорость сходимости при решении уравнений, для
которых значение модуля производной ½f ¢(x)½вблизи корня достаточно
велико, т.е. график функции y = f(x) в окрестности корня имеет большую
крутизну. Если кривая y = f(x) в интервале [a, b] почти горизонтальна, то
применять метод касательных не рекомендуется.
Существенным
недостатком рассмотренного метода является необходимость вычисления производных
функции для организации итерационного процесса. Если значение f ¢(x) мало изменяется на интервале [a, b], то для
упрощения вычислений можно пользоваться формулой
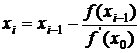 , (17)
, (17)
т.е.
значение производной достаточно вычислить только один раз в начальной точке.
Геометрически это означает, что касательные в точках Ci(xi,
f(xi)), где i = 1, 2, ..., заменяется прямыми,
параллельными касательной, проведенной к кривой y = f(x) в начальной точке
C0(x0, f(x0)).
В
заключение необходимо отметить, что все изложенное справедливо в том случае,
когда начальное приближение x0 выбрано достаточно близким к истинному корню x*
уравнения. Однако это не всегда просто осуществимо. Поэтому метод Ньютона часто
используется на завершающей стадии решения уравнений после работы какого-либо
надежно сходящегося алгоритма, например, метода половинного деления. Скорость
сходимости велика для простого корня и соответствует скорости геометрической
прогрессии для кратного корня.
Упрощенный вариант метода
Если
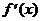 » const , то
» const , то 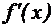 »
»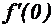 (см. рис. 9)
(см. рис. 9)
Рис.
9
Замечание.
Данный вариант метода актуален, если производная сложна.
Пример.
Необходимо методом касательных уточнить корень xÎ [0;1]
уравнения
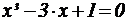 с
точностью 10 -3 (табл. 5) .
с
точностью 10 -3 (табл. 5) .
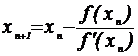 .
.
Таблица
5
|
N
|
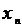 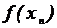 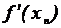 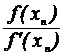
|
|
|
|
|
0
|
0
|
1
|
-3
|
-0,3333
|
|
1
|
0,3333
|
0,0371
|
-2,6667
|
-0,0139
|
|
2
|
0,3472
|
0,0003
|
-2,6384
|
-0,0001
|
|
3
|
0,3473
|
|
|
|
ïx 3 - x 2ï < e .
x » 0,347 .
. Метод хорд и касательных
Применяется только в том случае, когда f'(X) и f''(X) не изменяют знака
на отрезке [a,b], т.е. функция f(X) на отрезке [a,b] монотонна и не имеет точек
перегиба.
Суть метода та же самая - построение последовательности вложенных
отрезков, содержащих корень, однако отрезки строятся по-другому. На каждом шаге
через концы дуги графика функции f(X) на очередном отрезке проводят хорду и из
одного конца проводят касательную. Точки пересечения этих прямых с осью Оx и образуют следующий отрезок.
Процесс построения прекращают при выполнении того же условия:
(| b - a | < 2ε). (19)
Для того, чтобы отрезки получались вложенными, нужно проводить ту
касательную из конца, которая пересекает ось ОХ на отрезке [a,b]. Перебрав
четыре возможных случая, легко увидеть, что касательную следует проводить из
того конца, где знак функции совпадает со знаком второй производной.
Также несложно заметить, что касательная проводится либо все время из
правого, либо все время из левого конца. Будем считать для определенности, что
этот конец - b .
Формулы, употребляемые в методе, хорошо известны из аналитической
геометрии:
Уравнение хорды, проходящей через точки (a,f(a)) и (b,f(b)):
трансцендентное уравнение
дихотомия
y = f(a)+(x-a)*(f(b)-f(a))/(b-a),
откуда точка пересечения с осью Оx:
x= a - f(a) *(b-a)/(f(b)-f(a)).
Уравнение касательной, проходящей через точку (b,f(b)):
y=f(b)+f'(b)(x-b), откуда точка пересечения с осью Оx:
x= b -
f(b)/f'(b).
При составлении алгоритма снова естественно использовать для концов
отрезка только две переменные a и b и писать:
a= a - f (a) *(b-a)/ (f (b)-f (a)) (20)
b= b - f(b)/f'(b) (21)
Однако, в этом случае важен порядок формул (20) и (21).
Пример. Необходимо комбинированным методом уточнить корень xÎ[0;1] уравнения: х 3 - 3 × х +1 = 0, с точностью 10 -3 (табл.
6) .
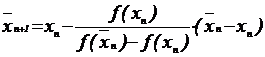 ,
,
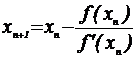 .
.
Таблица
6
n x n  f(x n)
f(x n) 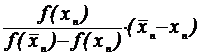
|
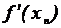 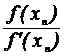
|
|
|
|
|
|
|
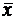 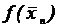
|
|
|
|
|
|
|
0
|
0
|
1
|
1
|
-0,5
|
-3
|
-0,3333
|
|
1
|
|
-1
|
|
|
|
|
1
|
0,3333
|
0,1667
|
0,0371
|
-0,0150
|
-2,6667
|
-0,0139
|
|
0,5
|
|
-0,3750
|
|
|
|
|
2
|
0,0011
|
0,0003
|
-0,0001
|
-2,6384
|
-0,0001
|
|
0,3483
|
|
0,0027
|
|
|
|
|
3
|
0,3473
|
0
|
|
|
|
|
|
0,3473
|
|
|
|
|
|
ê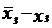 ê< e . x » 0,347 .
ê< e . x » 0,347 .
8. Заключение
Проблема повышения качества вычислений нелинейных уравнений при помощи
разнообразных методов существует, и будет существовать в дальнейшем. Ее решению
будет содействовать развитие информационных технологий, которое заключается как
в совершенствовании методов организации информационных процессов, так и их
реализации с помощью конкретных инструментов - сред и языков программирования.
9. Литература
. Вычислительная
техника и программирование: Учеб. для техн. вузов/ А.В. Петров, В.Е. Алексеев,
А.С. Ваулин и др. - М.: Высш. шк., 1990г. 479 стр. ISBN: 1522608, 1522607.
2. Гусев
В.А., Мордкович А.Г. - Математика: Справ. материалы: Кн. для учащихся. - 2-е
изд. - М.: Просвещение, 1990г. - 416 стр. ISBN 5-09-001292-X.
. Березин
В.Л., Харитонова К.Ю. «Просмотрщик решений трансцендентных уравнений и его
применение в задачах волоконной оптики», Сб. науч. тр. Механика. Математика,
Саратов: Изд-во Сарат. ун-та, 2004г. 168-170 стр.
. Мак-Кракен
Д., Дорн У. Численные методы и программирование на ФОРТРАНе. - М.: Мир, 1977г.
- 584 стр.
. Демидович
Б.П., Марон И.А. «Основы вычислительной математики». - М.: Наука, 1970г. - 664
стр.
6. <#"663909.files/image056.gif">
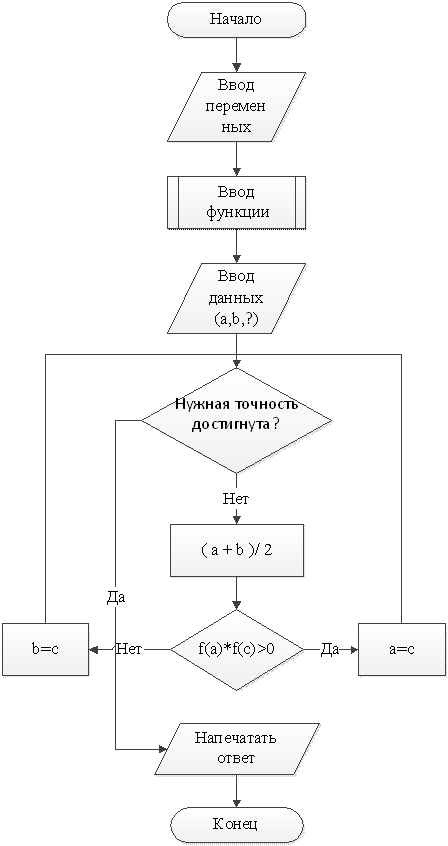
Блок схема программы: