|
№
|
Название
|
Каноническое
уравнение
|
|
Эллипсоид
|

|
|
Мнимый
эллипсоид
|

|
|
Мнимый
конус
|

|
|
Однополосный
гиперболоид
|

|
|
Двуполостный
гиперболоид
|

|
|
Конус
второго порядка
|

|
|
Эллиптический
параболоид
|

|
|
Гиперболический
параболоид
|

|
|
Эллиптический
цилиндр
|

|
|
Мнимый
эллиптический цилиндр
|

|
|
Две
мнимые пересекающиеся плоскости
|

|
|
Гиперболический
цилиндр
|

|
|
Две
пересекающиеся плоскости
|

|
|
Параболический
цилиндр
|

|
|
Две
параллельные плоскости
|
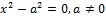
|
|
Две
мнимые параллельные плоскости
|

|
|
Две
совпадающие плоскости
|

|
В данной работе будем использована теорема,
сформулированная в предыдущей курсовой работе, но для трех переменных.
Именно произведем над переменными x, y, z целой
рациональной функции F второй степени от этих переменных

 (1)
(1)
Линейное неоднородное преобразование:

 (2)
(2)

Пусть

 (3)
(3)
функция, в которую при этом преобразуется
функция F. Тогда имеют место соотношения
 (4)
(4)

 (5)
(5)
В самом деле, квадратичная форма, входящая в
состав функции F, преобразует в квадратичную форму, входящую в состав функции
F’ при однородном преобразовании

 (6)
(6)

Отсюда следует формула (4)


при t’=1, а неоднородное преобразование (2)
получается из однородного:




при t’=1
Из этих соображений получается формула(5). Из
соотношений (4) и (5) следует, что при линейном преобразовании (2) над
переменными x, y, z целой рациональной функции F, при котором она переходит в
функцию F’, имеет место соотношения:
 (4’)
(4’)
 (5’)
(5’)
Определение:
Целая рациональная функция от коэффициентов
многочлена второй степени называется ортогональным инвариантом этого многочлена
относительно ортогонального преобразования, если она сохраняет свое значение
при неоднородных ортогональных преобразованиях переменных.
Теорема:
Функции *
 (7)
(7)
 (8)
(8)
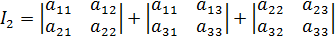 (9)
(9)
 (10)
(10)
являются ортогональными инвариантами целой
рациональной функции второй степени от трех аргументов:


Доказательство:
Так как определитель ортогонального
преобразования равен ±1, то его квадрат равен 1 и инвариантность I3 и K4
следует из соотношений (5’) и (4’).
Для доказательства того, что I2 и I1 также
являются ортогональными инвариантами, заметим, что коэффициенты  являются
инвариантами переноса:
являются
инвариантами переноса:
 (11)
(11)
Это доказывается так же, как и в предыдущей
курсовой работе.
Поэтому достаточно доказать, что I2 и I1
являются инвариантами однородного ортогонального преобразования:

 (12)
(12)

При этом преобразовании имеет место соотношение

Рассмотрим вспомогательную квадратичную форму

 (13)
(13)
При ортогональном преобразовании (12) она
перейдет в форму


По доказанному дискриминант квадратичной формы
является ортогональным инвариантом, значит,
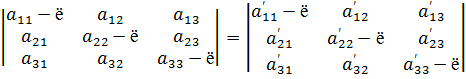
Это равенство верно при всех значениях  ,
следовательно, равны соответствующие коэффициенты при
,
следовательно, равны соответствующие коэффициенты при  и
и
 в
левой и правой частях т. е.
в
левой и правой частях т. е.



Теорема:
Функции
 (15)
(15)
 (16)
(16)
Являются инвариантами однородного
преобразования. Эти функции K3 и K2 называются «семиинвариантами»
(полуинвариантами).
Если же функция


однородным ортогональным преобразованием может
быть приведена к виду

то K3 является ортогональным инвариантом, а если
F однородным ортогональным преобразованием может быть приведена к виду
 , (18)
, (18)
то K2 (и K3) являются ортогональным инвариантом.
Доказательство:
Рассмотрим вспомогательную функцию


Производя однородное ортогональное
преобразование (12), получим функцию


По доказанному K4 ―ортогональный
инвариант. Используя это по отношению к функции Φ, получим

(тождество относительно λ).
Приравнивая
коэффициенты при λ и λ2
в
левой и правой частях, получим
 =
=

Предположим теперь, что существует однородное
ортогональное преобразование ω1, при
котором функция F переходит в функцию(17) семиинвариант K3 имеет значение
 (19)
(19)
равное его значению, вычисленному по формуле
(15). Определитель

не меняется, если над переменными x’ и y’
функции (17) совершить преобразование перенос

Пусть ω―произвольное
ортогональное преобразование. Рассмотрим ортогональное преобразование  тогда
тогда
 .
Далее, представим ортогональное преобразование ω’ в
виде произведения однородного ортогонального преобразования ω3
на перенос ω2; тогда
.
Далее, представим ортогональное преобразование ω’ в
виде произведения однородного ортогонального преобразования ω3
на перенос ω2; тогда  .
.
После однородного ортогонального преобразования ω1
функция
F перейдем в функцию (17) и по доказанному K3 не изменится и будем равен его
значению, вычисленному по формуле (19).
При преобразовании переноса ω2
функции
F’ перейдет в функцию

и по доказанному

наконец, после однородного ортогонального
преобразования ω3 функция F’’
перейдет в функцию
 и, следовательно,
и, следовательно, 
Аналогично доказывается, что K2 является ортогональным
инвариантом, если функция F однородным ортогональным преобразованием может быть
приведена к виду

Определение канонического уравнения.
В таблице указаны необходимые и достаточные
признаки того, что поверхность второго порядка является поверхностью I, II,
III, IV или V групп:
|
Номер
группы
|
Признак
группы
|
|
I
II III IV V
|
I3≠0 I3=0 K4≠0 I3=0 K4=0 I2≠0
I3=0 K4=0 I2=0 K3≠0 I3=0 K4=0 I2=0 K3=0 I1≠0
|
. Пусть поверхность второго порядка является
поверхностью I группы. Тогда, уравнение этой поверхности при помощи
преобразования прямоугольной системы координат в прямоугольную систему можно
привести к виду

где λ1≠0,
λ2≠0, λ3≠0. В таком случае

. Пусть поверхность второго порядка является
поверхностью II группы. Тогда её уравнение при помощи преобразования
прямоугольной системы координат в прямоугольную может быть приведено к виду

Где λ1 и
λ2
―отличные
от нуля корни характеристического уравнения (λ3=0) и
 .
Находим
.
Находим


. Пусть поверхность второго порядка является
поверхностью III группы. Тогда её уравнение при помощи преобразования
прямоугольной системы координат в прямоугольную может быть приведено к виду 
В данной таблице даны необходимые и достаточные
признаки каждого из семнадцати классов поверхностей второго порядка
|
№
|
Название
поверхности
|
Признак
|
|
|
1
|
Эллипсоид
|
I2>0
I1I3>0 K4<0
|
|
|
2
|
Мнимый
эллипсоид
|
I2>0
I1I3>0 K4>0
|
|
|
3
|
Мнимый
конус
|
I2>0
I1I3>0 K4=0
|
|
|
4
|
Однополосный
гиперболоид
|
I3≠0, K4>0 и
или
I2≤0 или I1I3≤0
|
|
|
5
|
Двуполостный
гиперболоид
|
I3≠0, K4<0 и
или
I2≤0 или I1I3≤0
|
|
|
6
|
Конус
второго порядка
|
I3≠0, K4=0 и
или
I2≤0 или I1I3≤0
|
|
|
7
|
Эллиптический
параболоид
|
I3=0,
K4<0
|
|
|
8
|
Гиперболический
параболоид
|
I3=0,
K4>0
|
|
|
9
|
Эллиптический
цилиндр
|
I3=0,
K4=0 I2>0 I1K3<0
|
|
|
10
|
Мнимый
эллиптический цилиндр
|
I3=0,
K4=0 I2>0 I1K3>0
|
|
|
11
|
Две
мнимые пересекающиеся плоскости
|
I3=0,
K4=0 I2>0 K3=0
|
|
|
12
|
I3=0,
K4=0 I2<0 K3≠0
|
|
|
13
|
Две
пересекающиеся плоскости
|
I3=0,
K4=0 I2<0 K3=0
|
|
|
14
|
Параболический
цилиндр
|
I3=0,
K4=0 I2=0 K3≠0
|
|
|
15
|
Две
параллельные плоскости
|
I3=0,
K4=0 I2=0 K3=0 K2<0
|
|
|
16
|
Две
мнимые параллельные плоскости
|
I3=0,
K4=0 I2=0 K3=0 K2>0
|
|
|
17
|
Две
совпадающие плоскости
|
I3=0,
K4=0 I2=0 K3=0 K2=0
|
|
|
Место
центров
|
Признак
место центров
|
Номер
класса
|
Признак
класса
|
Поверхность
|
Название
|
Каноническое
уравнение
|
|
Точка
|
I3≠0
|
1.
|
I2>0, I1I3>0,
K4<0
|

|
Эллипсоид
|

|
|
|
|
2.
|
I2>0, I1I3>0,
K4>0
|
|
Мнимый
эллипсоид
|

|
|
|
|
3.
|
I2>0, I1I3>0,
K4=0
|
|
Мнимый
конус
|

|
|
|
|
4.
|
K4>0 и
или
I2≤0 или
I1I3≤0
|

|
Однополосный
гиперболоид
|

|
|
|
|
5.
|
K4<0 и
или
I2≤0 или
I1I3≤0
|

|
Двуполостный
гиперболоид
|

|
|
|
|
6.
|
K4=0 и
или
I2≤0 или
I1I3≤0
|

|
Конус
второго порядка
|

|
|
Нет
центра
|
I3=0, K4≠0
|
7.
|
K4<0
|

|
Эллиптический
параболоид
|
 
|
|
|
|
8.
|
K4>0
|

|
Гиперболический
параболоид
|
 
|
|
Прямая
|
I3=0, K4=0,
I2≠0
|
9.
|
I2>0, I1K3<0
|

|

|
|
|
|
10.
|
I2>0, I1K3>0
|
|
Мнимый
эллиптический цилиндр
|

|
|
|
|
11.
|
I2>0, K3=0
|
|
Две
мнимые пересекающиеся плоскости
|

|
|
|
|
12.
|
I2<0, K3≠0
|

|
Гиперболический
цилиндр
|

|
|
|
|
13.
|
I2<0, K3=0
|

|
Две
пересекающиеся плоскости
|

|
|
Нет
центра
|
|
14.
|
I3=0, K4=0 I2=0,
K3≠0
|

|
Параболический
цилиндр
|

|
|
Плоскость I3=0,K4=0,I2=0,K3=0 15.
K2<0  Две
параллельные плоскости Две
параллельные плоскости 

|
|
|
16.
K2>0 Две
мнимые параллельные плоскости 

|
|
|
|
|
17.
|
K2=0
|
|
Две
совпадающие плоскости
|

|
|
|
|
|
|
|
|
|
|
|
|
Глава 2. Применение
теории инвариантов,уравнения линии второго порядка от трех переменных
Пример 1
Определить вид поверхности второго порядка:

Решение
I1=7, I2=0, I3=-36,
K4=36
Характеристическое уравнение:

Его коэффициенты: +1, -7, 36. Здесь имеются две
перемены знака: при переходе от +1 к -7 и от -7 к 36; значит, уравнение имеет
два положительных корня и один отрицательный. Кроме того,
 ;
;
следовательно, данная поверхность―
однополостный
гиперболоид.
Пример 2
Определить вид и расположение поверхности,
заданной относительно декартовой прямоугольной системы координат уравнением

Находим
I1=7,
I3=-36,
K4=36
Так как I1I3>0
K4<0,
то уравнение выражается однополостный гиперболоид. Далее I2=0.
Характеристическое уравнение:

имеет корни 𝛌1=3,
𝛌2=6,
𝛌3=-2






Î




 ;
;

Пример 3
Определить вид и расположение поверхности,
заданной относительно декартовой прямоугольной системы координат уравнением

Находим
1=5,
I2=6, I3=0, K4=0, K3=-12
I2>0,
I1K3<0

имеет корни 𝛌1=2,
𝛌2=3,
𝛌3=0














Пример 4
Определить вид и расположение поверхности,
заданной относительно декартовой прямоугольной системы координат уравнением

I1=1, I2=-6, I3=0,
K4=0, K3=0
Так как I3=0,
K4=0
I2>0
K3=0
то данное уравнение определяет пару пересекающихся плоскостей. Что бы
найти уравнения этих плоскостей, разложим левую часть данного уравнения на
линейные относительно x,
y, z
множители:







Отсюда находим уравнения плоскостей, на которые
распадается данная поверхность:

уравнение порядок переменная координата
Пример 5
Определить вид и расположение поверхности,
заданной относительно декартовой прямоугольной системы координат уравнением

Находим I1=5,
I2=-14, I3=0, K4=16
Данное уравнение выражает гиперболический
параболоид.
Характеристическое уравнение:

имеет корни 𝛌1=7,
𝛌2=-2,
𝛌3=0








 ,
,





Сначала находим 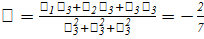 и
т.д.
и
т.д.
Пример 6
Определить вид и расположение поверхности,
заданной относительно декартовой прямоугольной системы координат уравнением

Находим I1=6,
I2=0, I3=0, K4=0, K3=-18
Данное уравнение является уравнением параболического
цилиндра. Перепишем его в виде:
Уравнения  являются
уравнениями прямоугольной образующей; из этих уравнений находим вектор
являются
уравнениями прямоугольной образующей; из этих уравнений находим вектор
 , коллинеарный
образующим.
, коллинеарный
образующим.
Координаты вектора  ,
идущего по единственному главному направлению, находим из системы:
,
идущего по единственному главному направлению, находим из системы:


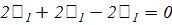

Наконец, вектор  ,
коллинеарный оси сечения параболического цилиндра плоскостью, перпендикулярной
образующим:
,
коллинеарный оси сечения параболического цилиндра плоскостью, перпендикулярной
образующим:

Простейшее
уравнение
а каноническое: 
Так как  ,
то вектор {1, 1, -1} направлен по оси сечения
,
то вектор {1, 1, -1} направлен по оси сечения

в сторону
выпуклости этой параболы.
Уравнение главной
диаметральной плоскости


Уравнения


являются уравнениями прямолинейной образующей,
по которой главная диаметральная плоскость пересекает данный параболический
цилиндр.
На этой образующей лежит, например, точка  .
Уравнение плоскости, касательной к параболическому цилиндру вдоль образующей λ,
имеет
вид
.
Уравнение плоскости, касательной к параболическому цилиндру вдоль образующей λ,
имеет
вид

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. М.В. Милованов, М.М. Толкачев,
Р.И. Тышкевич, А.С. Феденко Алгебра и аналитическая геометрия - Минск, 2001.
. П.С. Моденов Аналитическая
геометрия - Москва, 1969.