Законы случайных величин

Законы случайных величин

1. Дискретные системы двух случайных величин

Задача 1. По цели производиться два независимых выстрела. Вероятность попадания в цель при первом выстреле равна р₁=0.7, при втором р₂=0.8 . Рассматривается дискретная система двух случайных величин , где x - число попаданий при первом выстреле, h - число попаданий при втором выстреле.

Для рассматриваемой дискретной системы случайных величин  требуется:

а) описать закон распределения системы ;

б) описать законы распределения отдельных случайных величин, входящих в систему;

в) описать условный закон распределения случайной величины x при условии h = 1 и при этом условии вычислить условное математическое ожидание ;

г) выяснить, зависимы или нет случайные величины x и h;

д) вычислить вероятности  и >h);

е) вычислить основные числовые характеристики для системы :

.

Решение.

а) Для описания закона распределения дискретной системы двух случайных величин необходимо определить множество всех возможных пар значений

и соответствующие вероятности. Результат удобно представить в виде таблицы 2.1

Таблица 2.1

В первой строке указываются возможные значения случайной величины x, а в первом столбце - возможные значения случайной величины h; в последней строке и в последнем столбце указываются безусловные вероятности возможных значений соответственно случайных величин x и h. В каждой клетке таблицы, стоящей на пересечении i-го столбца и j-й строки, указываются вероятности совместного осуществления события

,

т. е.,

Заполним таблицу.

Занесем полученные данные в табл. 2.2

Таблица 2.2

По условию нормировки . Сделаем проверку:

Условие нормировки выполняется.

б) Законы распределения отдельных дискретных случайных величин, входящих в систему, получим из закона распределения дискретной системы случайных величин (см. табл. 2.2). Возможные значения случайных величин x и h известны, найдем соответствующие им вероятности. Для случайной величины x вероятности возможных значений определяются по формуле

,

т.е. суммируем вероятности «по столбцам»:

Аналогично для случайной величины h используем формулу

,

т.е. суммируем вероятности «по строкам»:

Законы распределения случайных величин x и h представим в виде ряда распределения для каждой величины (табл. 2.3, 2.4).

Таблица 2.3

Таблица 2.4

в) Условным законом распределения случайной величины x при условии, что величина h приняла определенное значение , называется совокупность возможных значений величины x и соответствующих этим значениям условных вероятностей 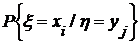, определяемых по формуле

. (1)

Условный закон распределения случайной величины x при условии, что величина h приняла значение, равное 1, находим по формуле (1), полагая h =0:

.

Тогда

Запишем условный закон распределения случайной величины x в виде ряда распределения (табл. 2.5).

Таблица 2.5

Используя данные табл. 2.5 и формулу условного математического ожидания случайной величины x при условии, что величина h приняла определенное значение :

вычислим условное математическое ожидание :

г) Установить зависимость или независимость случайных величин x и h, входящих в систему , можно, проверив необходимое и достаточное условие независимости

.

Так как

,

взять, например,

следовательно, случайные величины x и h независимы.

д) Вычислим вероятности

 и >h):

>h)=

е) Найдем основные числовые характеристики дискретной системы случайных величин x и h. Используя табл. 2.3 и 2.4, найдем  по формулам:

Корреляционный момент вычислим с помощью данных табл. 2.2 и следующей формулы:

Коэффициент корреляции определяется как отношение корреляционного момента к произведению среднеквадратичных отклонений случайных величин x и h :

Так как коэффициент корреляции , то можно утверждать, что случайные величины x и h линейно независимы.

2. Непрерывные системы двух случайных величин

Задача 2. Система случайных величин  задана совместной плотностью вероятности

в треугольной области АВС с координатами А(-1; 0), В(0; 1), С(-1; 2).

Требуется:

а) вычислить константу а в выражении для плотности вероятности ;

б) вычислить вероятность попадания случайной точки  в треугольную область АВD с координатами D(-1; 1);

в) найти безусловные плотности вероятности  и  случайных величин x и h;

г) найти условные плотности вероятности , ;

д) установить, являются ли случайные величины x и h независимыми;

е) вычислить основные числовые характеристики системы :

.

ж) найти условные математические ожидания  и  (случайной величины x относительно h и случайной величины h относительно x);

з) построить линии регрессии (x по h и h по x).

Решение.

Изобразим треугольную область АВС (рис. 2.1).

а) Для нахождения константы а в выражении для плотности вероятности , воспользуемся условием нормировки

Имеем

,

и, следовательно,

.

Напоминание. Площадь треугольника, построенного на векторах  и , равна

Рис. 2.1

б) Вероятность попадания равномерно распределенной в области D случайной точки  в некоторую область , найдем по формуле:

.

Точка D(0; 4) (см. рис. 2.1), следовательно,

.

в) Зная совместную плотность вероятности , можно найти безусловную плотность вероятности любой из случайных величин, входящих в систему  по формулам:

 = ,

 = .

Для расстановки пределов интегрирования в последних формулах составим уравнения прямых АВ, ВС и АС.

Напоминания: 1. Уравнение прямой, проходящей через две точки  и , имеет вид

2. Уравнение прямой в отрезках имеет вид

,

b - ордината точки пересечения прямой с осью Оу.

Уравнение прямой АВ имеет вид:

, .

Уравнение прямой ВС имеет вид:

, .

Уравнение прямой АС: .

Треугольник АВС не является областью, стандартной относительно оси  (см. рис. 2.1). Линия входа - отрезок прямой АВ (). Линия выхода - отрезок прямой ВС (), если .

Таким образом,

 = , если

Итак,

 =

Плотность вероятности  должна удовлетворять условию нормировки

.

Для его проверки построим график  (рис. 2.2).

Рис. 2.2

Площадь треугольника, ограниченного графиком  и осью Ох, равна 1. Следовательно, условие нормировки выполняется.

Треугольник АВС является областью, стандартной относительно оси Ох (см. рис. 2.1). Линия входа - отрезок оси Оу (), линия выхода - отрезок прямой АВ (), если , и отрезок прямой ВС ()

Таким образом,

 = , если

 = , если .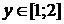

Итак,  

Для проверки условия нормировки  построим график  (рис. 2.3).

Рис. 2.3

Согласно рис. 2.3 площадь треугольника, ограниченного графиком  и осью Оу , равна 1. Следовательно, условие нормировки выполняется.

г) Условные плотности вероятности выражаются через безусловные по формулам:

 =  при ,

 =  при .

Следовательно,

Заметим, что условие нормировки  должно выполняться для любого фиксированного у, а условие нормировки  должно выполняться для любого фиксированного х.

д) Установить зависимость или независимость случайных величин x и h, входящих в систему , можно, сравнив условные ,  и безусловные ,  плотности, или, проверив необходимое и достаточное условие независимости =∙. В нашем случае  и , следовательно, x и h зависимы. Очевидно также, что ×, что подтверждает сделанный вывод.

е) Вычислим основные числовые характеристики системы :

 = ;

 = .

Заметим, что если система случайных величин  распределена равномерно в треугольной области АВС, где А(х₁, y₁), B(х₂, y₂), C(х₃, y₃), то

 = ,  = ;

(,) - так называемый центр рассеивания.

Проверим:

 = ,  = .

Для вычисления дисперсии  воспользуемся формулой

 = .

Вычислим второй начальный момент :

 = .

Тогда

 = .

Аналогично вычислим дисперсию случайной величины h :

 = .

Корреляционный момент , характеризующий связь между случайными величинами x и h, найдем по формуле

 = .

Для этого вычислим сначала второй смешанный начальный момент

 =

Тогда

 =

Безразмерной характеристикой связи между случайными величинами x и h служит коэффициент корреляции :

 = .

В рассматриваемом случае

 = .

Коэффициент корреляции  отражает «степень линейной зависимости» случайных величин x и h. Так как  = 0, x и h независимы.

ж) Условные математические ожидания случайных величин x и h, входящих в систему , найдем по формулам:

 =  и  = .

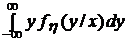Имеем:

 =

 =

Заметим, что в случае равномерного распределения системы  функции  и  являются линейными.

з) Построим линии регрессии, определяемые уравнениями  и . В рассматриваемой задаче

,

Рис. 2.4

Заметим, что линия регрессии  графически изображает зависимость «в среднем» случайной величины x от возможных значений случайной величины h. Аналогично для .

. Нормальный закон на плоскости

Задача 3. Случайная точка  распределена по нормальному закону с параметрами ,  Требуется:

а) написать выражение для плотности вероятности системы ;

б) изобразить на плоскости области  и вычислить вероятности попадания случайной точки  в эти области, если

,

,

,

,

;

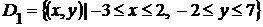в) вычислить вероятность  того, что при трех независимых опытах случайная точка попадет хотя бы один раз в область ;

г) вычислить вероятность  того, что при первых двух опытах случайная точка окажется хотя бы один раз в области , а при третьем опыте - в области ;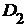

д) определить, какое минимальное количество опытов нужно произвести для того, чтобы случайная точка оказалась в области  с вероятностью не меньшей 0,95.

Решение.

а) Нормальный закон распределения для системы двух случайных величин  имеет плотность вероятности вида

,

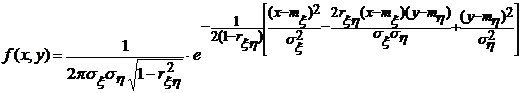где - математические ожидания случайных величин, - средние квадратические отклонения,  - коэффициент корреляции. Поэтому плотность вероятности данной системы имеет вид

.

б) Область  является прямоугольником с осями, параллельными главным осям рассеивания (рис. 2.5). По формуле

,

где  - функция Лапласа, значения которой находятся по таблице, вычисляем вероятность попадания случайной точки  в данную область:

Рис 2.5

Область 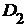 является прямоугольником с осями, параллельными главным осям рассеивания и центром в центре рассеивания (рис. 2.6).

Рис. 2.6

Следовательно, для вычисления искомой вероятности целесообразно применение формулы

Область  является квадрантом с вершиной в точке (-3-2) (рис.2.7).

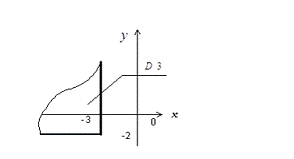
Рис. 2.7

Найдем вероятность попадания в область :

.

Область  является квадрантом с вершиной в центре рассеивания

Рис. 2.8

Искомую вероятность можно найти, исходя из симметричности поверхности распределения относительно плоскостей :

.

Вероятность попадания случайной точки  в эллипс рассеивания  (рис.2.9) вычисляем по соответствующей формуле:

,

где  - размеры полуосей эллипса рассеивания в единицах среднего квадратического отклонения по направлению главных осей рассеивания.

Рис. 2.9

случайный величина распределение дисперсия

в) Для определения вероятности  хотя бы одного попадания в область  при трех независимых опытах перейдем к противоположному событию, т.е. к тому, что в результате трех опытов случайная точка ни разу не окажется в области . Вероятность того, что случайная точка в результате опыта не попадет в область , равна

Затем находим вероятность того, что случайная точка при трех опытах ни разу не попадет в :

и, наконец, искомую вероятность:

г) Вероятность  того, что при первых двух опытах случайная точка окажется хотя бы один раз в области , а при третьем опыте - в области , равна по теореме умножения вероятностей произведению вероятности того, что при двух опытах случайная точка попадет хотя бы раз в область :

и вероятности попадания случайной точки в область :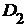

.

Итак, искомая вероятность

.

д) Если событие в каждом опыте может наступить с вероятностью , то количество  опытов, которые необходимо произвести для того, чтобы с вероятностью  можно было утверждать, что данное событие произойдет хотя бы один раз, находится по формуле

.

По условию, , тогда

,

т.е. необходимо провести как минимум 1 опыта.

4. Закон распределения функции одной случайной величины

Задача 4. Случайная величина x задана плотностью вероятности

Другая случайная величина h связана с x функциональной зависимостью h =. Требуется:

а) определить плотность вероятности  случайной величины h;

б) построить графики функций ,  и проверить условие нормировки для этих функций;

в) вычислить вероятность попадания случайной величины h в интервал .

Решение.

а) Функция  на отрезке [-2; 0] возможных значений случайной величины x монотонно возрастает и, следовательно, имеет обратную функцию , которая монотонно возрастает на отрезке  и является дифференцируемой. Поэтому искомую плотность вероятности найдем по формуле

.

Подставив сюда  и учитывая, что

, ,

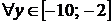получим

, если .

Таким образом, случайная величина h = имеет следующую плотность вероятности:

 =

б) Графики функций ,  приведены на рис. 2.10, 2.11.

Рис. 2.10                                Рис. 2.11

Проверим условия нормировки для функций  и:

,

Имеем:

,

в) Используя формулу , находим искомую вероятность:

Однако этот же результат можно получить, применяя формулу

, где

,  (здесь учтено, что функция

 убывает на отрезке .

Таким образом,

.

Итак,

.

5. Числовые характеристики функции одной случайной величины

Задача 5. Случайная величина x имеет плотность вероятности

Другая случайная величина h связана с x функциональной зависимостью

h =.

Требуется:

а) проверить условие нормировки для функции  и построить ее график;

б) вычислить математическое ожидание и дисперсию случайной величины h.

Решение.

а) Если функция  является плотностью вероятности случайной величины x , то она должна удовлетворять условию нормировки

.

Проверим его выполнение:

.

Строим график функции  (рис. 2.12).

Рис. 2.12

Замечание. Опущенные выкладки полного исследования функции  предлагается выполнить самостоятельно.

б) Способ 1. Для нахождения математического ожидания и дисперсии случайной величины  необязательно находить закон ее распределения; можно воспользоваться формулами

,

.

Учитывая, что , получим:

.

Замечание. Полученный результат  должен принадлежать интервалу возможных значений случайной величины h, т.е. .

Находим дисперсию:

.

Способ 2. Пользуясь определением математического ожидания функции случайного аргумента, его свойствами и указанными формулами (способ 1), получим:

.

Аналогично для дисперсии:

.

Итак, , .

6. Числовые характеристики функции двух случайных величин

Задача 6. Случайная величина x распределена равномерно в интервале (2;4), а независимая от нее случайная величина h распределена по нормальному закону с параметрами , . Требуется:

а) записать плотности вероятности  и  для случайных величин x и h;

;

в) вычислить математическое ожидание случайной величины

.

Решение

а) Так как случайная величина x имеет равномерное распределение, а h - нормальное распределение, то их плотности вероятности определяются соответственно выражениями:

Следовательно,

б) Запишем числовые характеристики исходных случайных величин:

, , ,

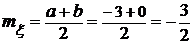Используя свойства математического ожидания и дисперсии функции случайных величин, получим:

;

Итак, искомые числовые характеристики

, .

в) Зная числовые характеристики исходных случайных величин, пользуясь свойствами и определением математического ожидания функции непрерывной случайной величины, имеем:

==.

Таким образом, .

7. Числовые характеристики функции трех случайных величин

Задача 7. Для системы трех случайных величин (,,) даны математические ожидания , ,  и корреляционная матрица

Требуется:

а) вычислить математическое ожидание и дисперсию случайной величины

;

б) вычислить математическое ожидание случайной величины

.

Решение

Согласно заданной корреляционной матрице имеем:

, , ;

, ,

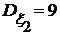Искомые числовые характеристики найдем, пользуясь свойствами математического ожидания, дисперсии и корреляционного момента:

а)

;

.

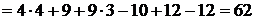Искомые характеристики , .

б)

=

.

Таким образом,

8. Характеристическая функция

Задача 8. Для данной плотности вероятности  найти характеристическую функцию  и с её помощью вычислить математическое ожидание .

Решение.

I способ. Воспользуемся методами операционного исчисления. Так как данная плотность вероятности  является оригиналом, то характеристическая функция  для неё является изображением. Найдём его, учитывая свойство линейности преобразования Лапласа и соотношение

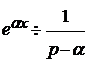, где

II способ. Характеристическую функцию  можно найти и по определению:

Вычислим , используя формулу . Имеем:

. Композиция законов распределения

Задача 9. Независимые случайные величины x и h распределены равномерно на отрезке [2; 4], т.е. их плотности вероятностей имеют вид:

Определить плотность вероятности  случайной величины , проверить условие нормировки для  и построить графики функций ,, .

Решение

Воспользуемся аппаратом характеристических функций и методами операционного исчисления. Для этого найдём характеристические функции  и  как изображения для плотностей вероятностей  и . Далее, учитывая независимость случайных величин x и , получим характеристическую функцию как произведение характеристических функций слагаемых случайных величин =∙. После этого, совершив обратное преобразование Лапласа, найдём искомую плотность вероятности  как оригинал для характеристической функции .

Найдём для  и  характеристические функции  и , используя свойства линейности преобразования Лапласа, запаздывания оригинала и операционное соотношение

где:

Следовательно,

Далее, используя свойство запаздывания оригинала и операционное соотношение , находим искомую плотность  как оригинал для характеристической функции  

Проверим условие нормировки для функции :

Графики функций ,,  приведены на рис. 2.13 - 2.15:

Рис. 2.13                                Рис. 2.14                      Рис. 2.15

. Предельные теоремы теории вероятностей

Задача 10. По полосе укреплений противника сбрасывается 108 серий бомб. При сбрасывании одной такой серии МО числа попаданий равно m=5, а . Пусть , i=-число попаданий в i-й серии , - общее число попаданий.

Требуется:

а) записать приближенное выражение для плотности вероятности  случайной величины h ;

б) вычислить приближенно вероятности: , ;

в) определить интервал наименьшей длины, симметричный относительно математического ожидания , в котором с вероятностью, не меньшей 0,9 будет заключена случайная величина h.

Решение

а) ,

Таким образом, плотность вероятности  случайной величины h приближенно равна

б) Используя формулу

,

где  - функция Лапласа, при , , получим

.

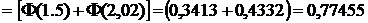Так как минимально возможное значение, принимаемое случайной величиной

h , равно 0, то

.

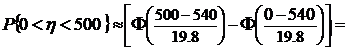
в) Обозначим через  половину длины наименьшего интервала, симметричного относительно математического ожидания , в котором с вероятностью, не меньшей 0,9, будет заключена случайная величина h. Тогда по условию.

Используя формулу

,

получим

.

По таблице значений функции Лапласа находим то значение аргумента х, для которого . Это значение приближенно равно

, откуда

.

Таким образом, искомый интервал наименьшей длины, симметричный относительно математического ожидания = 540, следующий:

, т.е. .

ЛИТЕРАТУРА

1. Е.И. Гурский. Высшая математика. Основы теории вероятностей случайных процессов и математической статистики. Изд. МВИЗРУ ПВО, 1983.

2.      Е.И. Гурский. Сборник задач по теории вероятностей и математической статистике. Минск «Вышэйшая школа», 1984.

.        А.А. Гусак, Е.А. Бричикова. Теория вероятностей. Справочное пособие к решению задач. Минск ТетраСистемс, 1999.

.        В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. М. «Высшая школа», 1975.

.        Е.И. Гурский, Т.В. Скобля, В.Э. Юшкевич. Методическое пособие по теории вероятностей и математической статистике. Изд. МВИЗРУ ПВО,1973.

.        Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под редакцией А.А. Свешникова. М.: Наука, 1970.

.        Сборник задач по математике. Теория вероятностей и математическая статистика. Под редакцией А.В. Ефимова. М.: Наука, 1990.