Численные методы решения задач

Аналитический вид функции

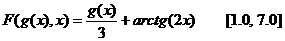
РЕШЕНИЕ

.        Строим аппроксимирующую зависимость  методом наименьших квадратов.

Последовательность действий при аппроксимации экспоненциальной зависимостью выглядит так:

-        вычисление логарифмов значений аппроксимируемой функции

         вычисление коэффициентов а и b по формулам ;

         вычисление коэффициентов с и d по формулам и ;

         вычисление значений g(x) по формуле .

Задание 1.1

При составлении расчетной таблицы был использован метод лианеризации. При этом обе части аппроксимируемой зависимости были подвергнуты процедуре логарифмирования.

Теперь рассчитываем коэффициенты уравнения по формулам:

Поэтому в соответствующие столбцы вводим формулы:

=A3^2 - для определения квадрата значения х.

=LN(B3) - для определения логарифма функции g(х).

=A3*D3 - для определения .

=СРЗНАЧ(A3:A22) - среднее значение х.

=СРЗНАЧ(B3:B22) - среднее значение g(х).

=СРЗНАЧ(D3:D22) - среднее значение логарифма функции g(х).

Теперь можно посчитать по соответствующей формуле d.

=(A24*D24-E24)/(A24^2-C24)

А затем определить значение с: =EXP(D24-E26*A24).

Аналитический вид функции g(х) имеет вид .

Теперь подсчитываем эмпирический ряд значений функции g(х) и вектор ошибок, возведенных в квадрат =(F3-B3)^2.

2. Строим график функции g(x)  с нанесенными на нем точками экспериментальных данных.

3. Строим график функции F(g(x),x)  на интервале [a; b], т.е. [1; 7].

2.      Вычисляем интеграл различными методами.

Делаем соответствующие расчеты в электронных таблицах Excel.

Задание 1.4

При определении интеграла функции  указанный участок следует разделить на 20 интервалов. Тогда шаг интегрирования будет составлять (7-1)/20=0,3.

=$A$2*EXP($B$2*A33)/3+ATAN(2*A33)

2.      Рассчитываем сумму по методу левых прямоугольников

3.      Рассчитываем сумму по методу правых прямоугольников

4.      Рассчитываем сумму по методу средних прямоугольников

5.      Переходим к методу трапеций. Здесь рассматриваем два варианта: с разбиением на 10 и на 20 интервалов.

.        Основные формулы для табличного счета имеют вид:

=$A$2*EXP($B$2*A33)/3+ATAN(2*A33) - расчет

=$A$2*EXP($B$2*D33)/3+ATAN(2*D33) - формула расчета функции для средних прямоугольников.

=$A$2*EXP($B$2*G33)/3+ATAN(2*G33) - формула для расчета функции для метода трапеций для 10 интервалов разбиения.

=$A$2*EXP($B$2*I33)/3+ATAN(2*I33) - формула для расчета функции для метода трапеций для 20 интервалов разбиения.

аппроксимирующий зависимость интеграл итерация

Уточнение по Ричардсону - это по сути экстраполяционный подход к пределу. Здесь следует рассчитывать значение функции по специальным формулам.

Рассчитываем более точно значение интеграла по методу Ричардсона. В соответствии с расчетами по методу трапеций имеем:

.        при разбиении участка интегрирования с h = 0,2 значение интегральной суммы  (St1);

.        при разбиении участка интегрирования с k = 0,1 значение интегральной суммы  (St2);

.        формулу для расчета метода трапеций , где

Вычисляем значение С:

Теперь можно получить более точное значение интеграла.

J = 10,02769 - 0,0284333 * 0,6 = 10,037925

Анализ вышеуказанной таблицы указывает, что наименьшим отклонением от истинного значения для рассматриваемой функции является метод средних квадратов. Метод трапеций дает несколько худший результат, но предположительно, что с уменьшением шага интегрирования может измениться и результат расчетов.

Задача 2

Методом простых итераций определить корень уравнения

,

где y(x) - решение задачи Коши

.

ПОСЛЕДОВАТЕЛЬНОСТЬ РЕШЕНИЯ ЗАДАЧИ 2

.        Решить на интервале [x_n, x_k] с разбиением его на 20 частей обыкновенное дифференциальное уравнение 1-го порядка  при начальных условиях  методом Эйлера и методом Рунге-Кутта 4-го порядка.

.        Построить графики найденных решений.

.        Из таблицы значений y(x), найденной для метода Рунге-Кутта 4-го порядка, для точки пересечения графика с осью абсцисс выбрать 4 последовательные точки, ближайшие к ней и расположенные по обе стороны от нее.

.        По выбранным четырем точкам построить интерполяционный полином Ньютона P₃(x) 3-го порядка.

.        Методом простых итераций с точностью e=0,001 найти корень уравнения P₃(x)=0 и рассматривать его как приближенное решение основной задачи работы.

Исходные данные

1.      Преобразуем дифференциальное уравнение

2.      Решаем дифференциальное уравнение указанными методами.

Результаты решения задачи показаны в таблице.

Задание 2.1

Решаем задачу по методу Эйлера с использованием формулы: . При решении задачи методом Эйлера используется следующий алгоритм: очередной аргумент ищется, как приращение по функции относительно предшествующего значения: =B7+$B$4*(SIN(A7)-B7/A7). Дальнейшие формулы имеют вид:

=C7+$B$4/2*((SIN(A7)-C7/A7)+(SIN(A8)-(C7+$B$4*(SIN(A7)-C7/A7))/A8))

Модиф. Метод Эйлера -

=D7+$B$4*(SIN(A7+$B$4/2)-(C7+$B$4/2*(SIN(A7)-C7/A7))/(A7+$B$4/2))

В методе Рунге-Кутта используется следующая формула:

здесь коэффициенты вычисляются по следующим формулам:

К0 - =$B$4*(SIN(A7)-I7/A7).

К1 - =$B$4*(SIN(A7+$B$4/2)-(I7+E8/2)/(A7+$B$4/2))

К2 - =$B$4*(SIN(A7+$B$4/2)-(I7+F8/2)/(A7+$B$4/2))

К3 - =$B$4*(SIN(A7+$B$4)-(I7+G8)/(A7+$B$4))

Итоговая формула имеет вид =I7+(E8+2*F8+2*G8+H8)/6.

3.      Строим графики найденных решений.

4.      Выбираем из таблицы 4 последовательных точки y(x).

5.      По выбранным четырем точкам строим интерполяционный полином Ньютона.

6.      Находим корни уравнения P₃(x)=0 с точностью e=0,001.

Получен полином следующего вида:

Подставляем значения х из таблицы и получаем:

После преобразования получаем:

Найдем корень этого уравнения на интервале [2,095; 2,35] методом простых итераций. Для этого продифференцируем найденное уравнение:

Условием сходимости метода простых итераций является выполнение в окрестности искомого корня неравенства .

Проверяем это условие:

Для поиска корня методом простых итераций преобразуем найденный полином к виду . Поэтому выполняем следующие преобразования:

Продифференцируем функцию :

Из условия сходимости метода следует:

Так как в левой части стоит модуль, то оно распадается на два неравенства:

Из первого неравенства следует, что С<0.

Преобразуем второе неравенство: . Подставляем в это выражение значения х, равное границам интервала определения корней (2,095 и 2,35). Соответственно получаем: С> -2,5 и С>-1,6. Выбираем большее из этих двух значений и окончательно получаем:

,6 < C < 0.

Выбираем значение С из этого интервала: С = - 1