Компьютерное моделирование дифракции упругих волн на локальных неоднородностях

Компьютерное моделирование дифракции упругих волн на локальных неоднородностях

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «КубГУ»)

Кафедра вычислительных технологий

ДОПУСТИТЬ К ЗАЩИТЕ В ГАК

Заведующий кафедрой академик РАН,

д-р физ.-мат. наук, профессор

_______________________Миков А.И.

(подпись)   (инициалы, фамилия)

_______________________2013г.

ДИПЛОМНАЯ РАБОТА

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ДИФРАКЦИИ УПРУГИХ ВОЛН НА ЛОКАЛЬНЫХ НЕОДНОРОДНОСТЯХ

Работу выполнил                                                                        А.А.Дмитренко

Факультет                     ФКТиПМ

Специальность            010501 - Прикладная математика и информатика

Научный руководитель,

профессор, д.ф.-м.н.                                                                       Е.В. Глушков

Нормоконтролер

доцент, канд. физ.-мат наук                                                           Е.А. Данилов

Краснодар 2013

СОДЕРЖАНИЕ

Введение

. Общие понятия

.1 Упругие волны

.2 Волновое уравнение

.3 Дифракция волн

. Численные методы

.1 Метод коллокаций

.2 Метод конечных элементов

.3 Метод граничных элементов

. Постановка задачи

.1 Общая схема решения задачи

.2 Описание программной реализации

.3 Численные примеры

Заключение

Список использованных источников

Приложение

ВВЕДЕНИЕ

Неразрушающий контроль (НК) - контроль надежности и основных рабочих свойств и параметров объекта или отдельных его элементов - узлов, не требующий выведение объекта из работы, либо его демонтажа.

В данной дипломной работе будет рассматриваться акустический метод неразрушающего контроля. А именно ультразвуковая дефектоскопия - метод предложенный С. Я. Соколовым <#"655872.files/image001.jpg">

Скорость распространения волны зависит от свойств среды, а также от типа волны (продольные и поперечные волны распространяются с разной скоростью). Демонстрация с пружиной. Наиболее просто математически описываются синусоидальные волны. Они широко распространены в природе и, что особенно важно, все другие волны можно представить в виде суммы большого числа синусоидальных волн. Синусоидальную волну в длинном шнуре можно получить, если один из концов струны заставить совершать гармонические колебания. Уравнение такой волны описывается формулой

 (1)

где y(x,t)- смещение из положения равновесия точки шнура с координатой x в момент времени t, A - амплитуда волны, ω - циклическая частота, k - так называемое волновое число, α - начальная фаза. Каждая точка шнура совершает гармонические колебания в направлении оси y. Начальная фаза этих колебаний

линейно зависит от координаты точки x: чем дальше от источника расположена точка шнура, тем сильнее «запаздывают» ее колебания. При t = const формула (1) дает мгновенную «фотографию» шнура - его положение в данный момент времени в пространстве:

,

где ψ =ωt +α. График y(x)имеет синусоидальную форму с пространственным периодом λ = k /2π. Эту величину называют длиной волны. Длина волны - это расстояние между точками, которые колеблются с фазовым сдвигом, равным 2π. Точки струны, расположенные на расстоянии λ друг от друга, колеблются одинаково: одновременно достигают максимума, одновременно проходят через ноль.

Рис.1

На рис.1 изображены положения струны в три последовательных промежутка времени t: t +T /4 и t +T /2 . Видно, что за время T /2 максимум колебаний сместился в направлении оси x на Δx = λ/2. Скорость перемещения максимума (постоянной фазы) равна

 .

Это и есть скорость волны (фазовая скорость). Скорость волны зависит от свойств среды, в которой она распространяется и от типа волны (поперечная или продольная). Формула (1) описывает не только поперечные волны, но и продольные. В этом случае величина y имеет смысл смещения частицы из положения равновесия не в поперечном, а в продольном направлении. Геометрическая картина продольной волны менее наглядна: вдоль шнура-пружины теперь распространяются области растяжения и сжатия. Однако смысл всех величин остается прежним. Уравнение волны принято записывать в виде

где ξ(x,t) - смещение точки с координатой x из положения равновесия в момент времени t. Это уравнение описывает не только волны в струне, но и любую волну (например, звуковую), распространяющуюся вдоль оси x.

1.3 Дифракция волн

Дифракция волн - явление, которое проявляет себя как отклонение от законов геометрической оптики <#"655872.files/image008.gif">, удовлетворяющую линейному дифференциальному уравнению

+q(x)y=f(x)            (2)

и линейными краевыми условиями

 , (3)

причем .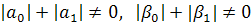

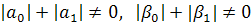Выберем некоторую совокупность линейно независимых функций

которую назовем системой базисных функций.

Пусть функция  удовлетворяет неоднородным краевым условиям

а остальные функции удовлетворяют соответствующим однородным краевым условиям:

Если краевые условия (3) однородны (A=B=0), то можно положить  и рассматривать лишь систему функций.

.             (4)

Тогда функция y удовлетворяет краевым условиям (3). В самом деле, в силу линейности краевых условий имеем

)=A+

и аналогично

Составим функцию . Подставляя сюда вместо y выражение (4), будем иметь

.

Если при некотором выборе коэффициентов ci выполнено равенство

 при

то функция y является точным решением краевой задачи (2), (3). Однако подобрать так удачно функции  и коэффициенты ci в общем случае не удается. Поэтому ограничиваются тем, что требуют, чтобы функция  обращалась в нуль в заданной системе точек  из интервала [a, b], которые называются точками коллокации. Сама функция R называется невязкой уравнения (2). Очевидно, что в точках коллокации дифференциальное уравнение (2) будет удовлетворено точно, и невязка в этих точках равна нулю.

Итак, метод коллокации приводит к системе линейных уравнений

 . (5)

Из системы (5) в случае ее совместности можно определить коэффициенты (, после чего приближенное решение краевой задачи дается формулой (4).

2.2 Метод конечных элементов

Метод конечных элементов (МКЭ) - численный метод решения дифференциальных уравнений с частными производными <#"655872.files/image031.gif">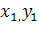) в первом случае представляет собой полость квадратной формы со стороной с. В данной задаче будут рассмотрены SH-колебания( поперечно-горизантальные поляризационные волны). На данном рисунке изображена пластина прямоугольной формы с простой неоднородностью, ввиде квадратного отверстия. В левом верхнем углу находится актуатор.

Рис.2

Данные волны описываются следующим уравнением:

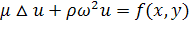
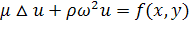 (6)

где - частота,

- плотность материала среды,

- коэффициент сдвига,

- смещение.

 моделирует действие актуатора( источник волн):

.

На границах среды заданны условия

Согласно МГЭ(метод граничных элементов) будем представлять решение в виде:

 ,                  (7)

где - поле источника в безграничной среде:

,

- фундаментальное решение уравнения Геймгольца:

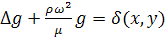
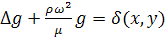
определено в явном виде

,

 функция Ханкеля 1 рода нулевого порядка.

Представление (7) удовлетворяет (6) автоматически в рассматриваемой области за исключением границ. Удовлетворяя нашим граничным условиям, подставим (7) в граничные условия и получим производные имеющие общий вид:

Подставляя их в граничные условия получим интегральные уравнения:

упругий волна дифракция ультразвуковой

Будем решать интегральные уравнения МГЭ(метод граничных элементов).

Удовлетворяя условию на границах получим:

Полученные функциональные уравнения будем решать методом коллокаций. Пусть узлы точек коллокаций совпадают с узлами точек базисных функций. Метод коллокаций приводит к СЛАУ, где

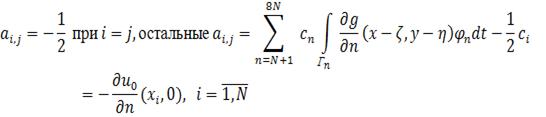
3.1 Описание программной реализации

Моя модель была создана в пакете Comsol Multyphysics 4.2a.

На рис.3, приведенном ниже, изображено тело программы со всеми используемыми модулями.

Рис.3

При создании проекта в первую очередь указывается система измерения. Была выбрана безразмерная система измерения. Во вкладке Definitions задаются параметры координатного пространства. В Geometry строится заданная исследуемая модель. В Materials задаются данные об используемых материалах: плотность и модуль сдвига. Следующая вкладка это Helmholtz Equation, в ней мы задаем параметры для решения нашей волновой задачи.

Решение выводится в такой рабочей плоскости, изображенной на рис.4, где можно менять масштаб, сделать скриншот и развернуть график.

Рис.4

3.2 Численные примеры

Ниже приведена таблица 1, построенная на данных вышеизложенных примеров.

Таблица 1 - значения U(смещения)

Моделируя различные примеры с на разных материалах можно выявить некоторые закономерности.

-       Наличие препятствий существенно искажает волновую картину

-       Увеличение частоты приводит к уменьшению более активной зоны смещения

-       При перемещении актуатора в центр пластины нижний предел значения смещения увеличивается

-       Наличие множества неоднородностей уменьшают верхний предел значения смещения

-       Повышение частоты значительно уменьшает зону смещения

Опираясь на выявленные закономерности мы можем значительно упростить процесс дефектоскопии на данных материалах, так как подобрали оптимальный диапазон частот при которых наиболее эффективна работа дефектоскопа.

ЗАКЛЮЧЕНИЕ

В данной дипломной работе были рассмотрены общие понятия о неразрушающем методе контроля, дифракции упругих волн и численных методах решения. Проведено исследование волновой картины на неоднородных участках.

Сделана попытка создать адекватную модель дифракции упругих волн в неоднородной среде, а также смоделировать частотный спектр волновой картины.

Реализована возможность моделирования дифракции упругих волн на локальных неоднородностях для любых материалов. Для проведения экспериментов было написано Windows-приложение с достаточно широкими возможностями исследования волновой картины в телах любых материалов.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.      Линьков А.М. Комплексный метод граничных интегральных уравнений теории упругости. СПб.: Наука, -1999. - 382 с. 51ил.

.        Лифанов И.К. Метод сингулярных интегральных уравнений и численный эксперимент (в математической физике, аэродинамике, теории упругости и дифракции волн). М.: ТОО Янус, -1995. - 520 с.

.        Купрадзе В.Д. Методы потенциала в теории упругости. М.: Государственное издательство физико-математической литературы, - 1963. - 472 с.

4.      Сайт «Википедия свободная энциклопедия». #"655872.files/image068.gif">

На первом рисунке изображена пластина с неоднородностью квадратной формы.

Рис.5

Шкала справа отображает u(смещение). На рис.5 отчетливо видим искажение волновой картины в районе препятствия. Шкала координатной оси измеряется в метрах.

Рис.6

На Рис.6 смоделировано несколько препятствий(пустот), так же был перемещен актуатор, как видим волновая картина в данном случае кардинально поменялась. Множество препятствий сильно искажают волновую картину. В следствие всех этих изменений понизилось смещение, это можно наблюдать по шкале, справа от рисунка.

На Рис.7 была увеличена частота , по сравнению с предыдущими примерами, как видим, волновая картина не изменилась, но сущесвенно уменьшилось смещение. Шкала справа от графика отображает u(смещение).

Рис.7

Как мы можем наблюдать по приведенным выше примерам, препятсвия мешают ровному и однородному распрастранению упругих волн на пластине. Так же заметим, что при увеличении частоты волн смещение уменьшается, это говорит о том, что высокочастотные волны в данном материале распрастраняются заметно хуже, чем волны с более низкими частотами.

Далее будут рассмотрены примеры для пластин этих же размеров с такими же неоднородностями для других материалов, в частности стали и титана.

Теперь рассмотрим пример на пластине из стали. Параметры для этого сплава брались средние. , .

На рис.8 видим незначительное изменение волновой картины, расширилось поле смещения от эпицентра к границам пластины.

Рис.8

Заметим, что из-за высокой плотности стали, значения смещения намного меньше, чем у алюминиевой пластины.

На рис.9 с множеством препятствий видим сильное искажение волновой картины. Значения смещения по сравнению с предыдущим примером уменьшились примерно на 15%, это следствие того, что препятствия мешают распрастранению волн по плоскости пластины

Рис.9

На рис.10 можем наблюдать явление, характерное и для первого примера с алюминиевой пластиной, а именно уменьшение значений смещения в пластине в следствии увеличения подаваемой частоты на актуатор .

Рис.10

В последнем примере рассмотрим пластину из титана. Входные данные для этой модели равны:  Заметим, что особенностью этого примера является то, что плотность этого материала существенно ниже приводимых выше материалов.

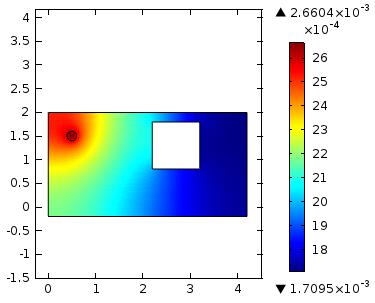
Рис.11

На рис.11 мы можем наблюдать расширение зоны смещения, но так же и уменьшение значений смещения. В данном случае это объясняется необычайно низкой плотностью материала. Что касается зоны смещения, то ее расширение обусловлено большим модулем сдвига для данного материала.

На рис.12 наблюдаем искажение волной картины, обусловленное наличием множества неоднородностей. Заметим, что значения смещения уменьшились примерно на 10%

Рис.12

Рассмотрим следующий пример с увеличением частоты на актуаторе в 3 раза, . На рис.13 можем наблюдать характерное уменьшение зоны более активного смещения. Так же значения смещения уменьшились почти на 50%.

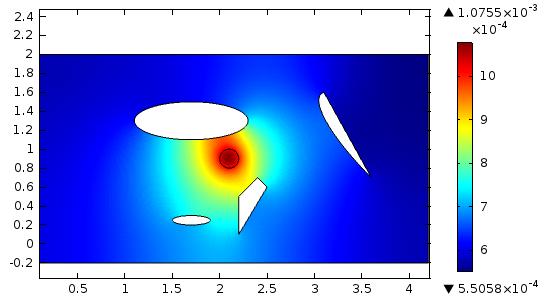
Рис.13