О некоторых свойствах ганкелевых операторов над группами
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение
образования
«Гомельский
государственный университет
имени
Франциска Скорины»
Математический факультет
Кафедра
математического анализа
О некоторых
свойствах ганкелевых операторов над группами
Курсовая
работа
Исполнитель:
студент группы М-41 _____________Дыба Р.В.
Гомель 2012
г.
СОДЕРЖАНИЕ
Введение
. Полухарактеры и характеры
.1 Начальные сведения
.2 Двойственность Понтрягина
.3 Функциональная характеристика показательной функции
.4 Полугруппа Sp
.4.1 Определение и некоторые свойства
.4.2 Инвариантная мера в Sp
.4.3 Полухарактеры и характеры в Sp
.5 Полугруппа S
.5.1 Определение и некоторые свойства
.5.2 Инвариантная мера в S
.5.3 Полухарактеры и характеры в S
. Операторы Ганкеля
.1 Определения матрицы и оператора Ганкеля
.2 Ганкелевы операторы в пространствах Харди
.3 Символы операторов Ганкеля и Теорема Нехари
Заключение
Список использованных источников
ВВЕДЕНИЕ
Целью данной курсовой работы является изучение
некоторых полугрупп, возникающих в статистических вычислениях и их свойств, и
некоторых свойств ганкелевых операторов над ними. В работе рассмотрен вопрос о
введении в них инвариантной меры, а также находится общий вид полухарактеров и
характеров двух полугрупп, имеющих немаловажное значение и использующихся в
анализе на полумодулях. Также в данной работе рассмотрен основной пример
оператора Ганкеля и изучены некоторые его свойства.
1. ПОЛУХАРАКТЕРЫ И ХАРАКТЕРЫ
.1 Начальные сведения
Частичным ассоциативным группоидом называют систему,
состоящую из непустого множества S и
отображения т(х,у) = ху (закона композиции), действующего из непустого
подмножества произведения S x S в S и
обладающего свойством ассоциативности. Если т определено не на всем
произведении S x S, то S
называют полугруппой. Полугруппа S
называется абелевой (коммутативной), если ху = ух при всех х, у Î S. Далее мы будем, как правило, иметь дело с полугруппами.
Левым (правым) идеалом полугруппы S называется такое непустое
подмножество AÍ S, что saÎA (asÎA) при всех sÎS, аÎА. Если А является и левым, и правым
идеалом полугруппы S, то его называют
(двусторонним) идеалом. Идеал полугруппы S называется простым, если его дополнение есть полугруппа.
Говорят, что подмножество Р полугруппы S обладает левыми (правыми)
сокращениями на элементы S,
если из равенства
sx = sy (xs = ys), где sÎS,
x, уÎP, следует равенство х = у. Мы скажем, что S - полугруппа с (двусторонними)
сокращениями, если она обладает и левыми, и правыми сокращениями.
Группа G
называется группой левых частных полугруппы S, если S
погружается в G, и каждый элемент xÎG представляется в виде
х =а-1b,
где a,bÎS. Известно (теорема Оре), что
полугруппа S погружается в группу левых частных
тогда и только тогда, когда она обладает сокращениями и реверсивна справа, т.
е. Sa ∩Sb ≠ 0 для любых a, bÎ S. В частности, любая коммутативная полугруппа с сокращениями
погружается в группу частных.
Полугруппа
S, наделенная хаусдорфовой топологией, для которой
отображение т(х,у) = ху из S S в S
непрерывно, называется топологической полугруппой.
S в S
непрерывно, называется топологической полугруппой.
Топологическая
группа - это топологическая полугруппа, являющаяся группой, в которой
непрерывна также и операция перехода к обратному элементу. Топологическая
группа называется локально компактной, если ее топологическое пространство
локально компактно.
Скажем,
что топологическая полугруппа S погружается в топологическую группу G,
если существует взаимно-непрерывный инъективный гомоморфизм р: S → G. При этом,
когда это удобно, мы будем отождествлять S с ее образом p(S) в
группе G. В этом случае группа S ∩ S -1
обратимых элементов полугруппы S будет обозначаться G(S).
Если
X - топологическое пространство, то наименьшая σ-алгебра β(Х) его подмножеств, содержащая все открытые множества, называется σ -алгеброй борелевских множеств. Мера μ, определенная на σ -кольце  Í β(Х), называется внутренне регулярной, если для любого ВÎ
Í β(Х), называется внутренне регулярной, если для любого ВÎ  имеем
имеем
μ (B) = sup{μ (C):СÍ В,С Î
 ,С компактно}.
,С компактно}.
Мера
на β(Х) называется борелевской мерой. Борелевская мера на
хаусдорфовом пространстве X называется мерой Радона, если она внутренне
регулярна, и меры всех компактных множеств конечны.
Левой
мерой Хаара на локально компактной группе G называется
мера Радона μ, инвариантная в том смысле, что μ(хВ) = μ(В) для любых ВÎ
β
(Х),
хÎ G. Известно (А. Хаар, А. Вейль),
что левая мера Хаара всегда существует и единственна с точностью до множителя.
То же верно для правой меры Хаара. Если группа абелева, то просто говорят о
мере Хаара на группе G.
Пусть
теперь S - топологическая полугруппа (не обязательно абелева).
Полухарактером полугруппы S будем называть непрерывный гомоморфизм из S в
полугруппу 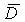 с операцией умножения (
с операцией умножения (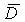 -
единичный диск комплексной плоскости), отличный от тождественно нулевого.
Пространство всех полухарактеров полугруппы S, наделенное
топологией поточечной сходимости, будет обозначаться S*, а его подпространства,
состоящие из всех вещественнозначных (положительных, ограниченных
положительных) полухарактеров, - через Sr*
(соответственно S+*, S1*).
-
единичный диск комплексной плоскости), отличный от тождественно нулевого.
Пространство всех полухарактеров полугруппы S, наделенное
топологией поточечной сходимости, будет обозначаться S*, а его подпространства,
состоящие из всех вещественнозначных (положительных, ограниченных
положительных) полухарактеров, - через Sr*
(соответственно S+*, S1*).
Для
топологической полугруппы S через S^ обозначим множество всех ее ограниченных
полухарактеров (т. е. ненулевых непрерывных гомоморфизмов из S в
замкнутый единичный диск  комплексной плоскости с операцией умножения),
наделенное топологией равномерной сходимости на компактных подмножествах S, а
через S^+ - подпространство этого пространства,
состоящее из неотрицательных полухарактеров (разумеется, в дискретном случае
комплексной плоскости с операцией умножения),
наделенное топологией равномерной сходимости на компактных подмножествах S, а
через S^+ - подпространство этого пространства,
состоящее из неотрицательных полухарактеров (разумеется, в дискретном случае
S1* = S^+).
Характером
будем называть полухарактер, равный по модулю единице, а группа характеров
будет обозначаться X.
Следует
отметить, что даже в случае абелевых полугрупп с сокращениями множества S*, S+*, S^, S^+ и ряд их множеств являются относительно
поточечного умножения лишь частичными ассоциативными группоидами.
(Действительно, пусть, например, S есть мультипликативная полугруппа 2
 3
3 . Тогда индикаторы множеств 2
. Тогда индикаторы множеств 2 \ 3
\ 3 и 3
и 3 \ 2
\ 2 принадлежат S^+, но их произведение равно нулю). Тем не
менее, все эти группоиды являются полугруппами, если S содержит
единицу.
принадлежат S^+, но их произведение равно нулю). Тем не
менее, все эти группоиды являются полугруппами, если S содержит
единицу.
.2
Двойственность Понтрягина
Пусть
G - коммутативная группа. Как было определено выше,
характером этой группы называется гомоморфизм G в группу Т
(единичную окружность комплексной плоскости), т. е. такая функция  на G с комплексными значениями, равными 1 по абсолютной величине,
что
на G с комплексными значениями, равными 1 по абсолютной величине,
что
 (х + у) =
(х + у) =
 (х)
(х) (у). (1)
(у). (1)
Если
G - топологическая группа, то, как правило, термин
«характер» означает «непрерывный характер». Мы будем считать все
рассматриваемые характеры непрерывными, не оговаривая этого особо. Если  и
и  -
характеры группы G, то их произведение
-
характеры группы G, то их произведение  - также
характер; если
- также
характер; если  - характер, то
- характер, то
 (комплексное
сопряженное) - также характер. Таким образом, совокупность всех характеров
данной группы G образует группу относительно операции обычного
умножения функций. Эта группа обозначается G^ и называется
группой, двойственной к G. Группа G становится топологической
группой, если определить сходимость
(комплексное
сопряженное) - также характер. Таким образом, совокупность всех характеров
данной группы G образует группу относительно операции обычного
умножения функций. Эта группа обозначается G^ и называется
группой, двойственной к G. Группа G становится топологической
группой, если определить сходимость  как
равномерную сходимость на каждом компакте K
как
равномерную сходимость на каждом компакте K G.
G.
Пример.
Пусть
G =  - группа
целых чисел. Ясно, что каждый характер
- группа
целых чисел. Ясно, что каждый характер  G^
определяется своим значением на образующем элементе 1
G^
определяется своим значением на образующем элементе 1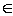 G (не путать 1 с единицей группы, роль которой играет
0). В самом деле, из (1) следует, что
G (не путать 1 с единицей группы, роль которой играет
0). В самом деле, из (1) следует, что
 для всех
для всех
 , (2)
, (2)
Значение
 может быть любым числом
может быть любым числом  Т. Тем самым множество G
отождествляется в этом случае с окружностью Т.
Т. Тем самым множество G
отождествляется в этом случае с окружностью Т.
Теорема.
Имеет место изоморфизм топологических групп  ^ = Т.
^ = Т.
Доказательство.
Мы уже видели, что множество  естественно
отождествляется с Т. Покажем, что это соответствие является изоморфизмом
топологических групп. Будем обозначать через
естественно
отождествляется с Т. Покажем, что это соответствие является изоморфизмом
топологических групп. Будем обозначать через  характер,
определяемый условием
характер,
определяемый условием  ,
,  Т. Равенство
Т. Равенство  показывает,
показывает,
что
соответствие  является изоморфизмом групп Т и
является изоморфизмом групп Т и  ^. Осталось проверить, что это соответствие является
гомеоморфизмом. Поскольку группа
^. Осталось проверить, что это соответствие является
гомеоморфизмом. Поскольку группа  дискретна,
каждый компакт в
дискретна,
каждый компакт в  состоит из конечного числа точек. Значит, сходимость
в
состоит из конечного числа точек. Значит, сходимость
в  является поточечной сходимостью. Равенство (2)
показывает, что
является поточечной сходимостью. Равенство (2)
показывает, что 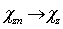 тогда и только тогда, когда
тогда и только тогда, когда  , т. е. когда
, т. е. когда  . Теорема
доказана.
. Теорема
доказана.
Также
можно доказать, что группа Т^ изоморфна . Тогда
получаем, что группы
. Тогда
получаем, что группы  и Т двойственны друг к другу. Этот факт является
частным случаем принципа двойственности Л. С. Понтрягина:
и Т двойственны друг к другу. Этот факт является
частным случаем принципа двойственности Л. С. Понтрягина:
Для
любой локально компактной топологической группы G естественное
отображение G в (G^)^, которое элементу g G ставит в
соответствие характер fg на G^ по формуле
G ставит в
соответствие характер fg на G^ по формуле
 ,
,  G^,
G^,
является
изоморфизмом топологических групп.
1.3
Функциональная характеристика показательной функции
Для
нахождения характеров нам понадобится решать уравнения вида (1). Однако вначале
рассмотрим задачу:
Найти
все непрерывные в промежутке  функции f(x),
удовлетворяющие условию
функции f(x),
удовлетворяющие условию
f(x+y) = f(x) + f(y),
(3)
каковы
бы ни были значения x и у.
Уравнение
(3) является простейшим примером так называемых функциональных уравнений,
формулирующих некое свойство искомой функции, по которому она и должна быть
найдена. Наша задача состоит в отыскании всех непрерывных решений уравнения
(3).
Легко
видеть, что линейные однородные функции вида
f(x) = cx ( c=const) (4)
удовлетворяют
этому уравнению. Покажем, что они будут единственными непрерывными функциями,
имеющими свойство (3).
Прежде
всего, с помощью метода математической индукции легко обобщить соотношение (3)
на случай любого числа (=n) слагаемых:
 = f(x) + f(y) +…
+ f(z) (5)
= f(x) + f(y) +…
+ f(z) (5)
Действительно,
если допустить верность его для какого-либо числа n 2 слагаемых, то оно окажется верным и для n+1
слагаемых:
2 слагаемых, то оно окажется верным и для n+1
слагаемых:
 ,
,
Полагая
в (5) x = y = … = z, найдем:
f(nx) = n f(x).
(6)
f(x).
(6)
Заменив
здесь x на 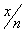 , получим
, получим
 ,
,
А
затем, если подставить mx ( m- натуральное) вместо x и использовать
предыдущее равенство, придем к соотношению
 (7)
(7)
Положим
теперь в основном уравнении (3) x = y = 0; получим
f(0) = 2 f(0), откуда f(0)=0.
(8)
f(0), откуда f(0)=0.
(8)
Если
же взять y = - x, то, с учетом (8) найдем:
f(-x) =
- f(x),
т.
е. функция f(x) нечетная, тогда из (6) и (7) легко получить:
f(-nx) =
- f(nx) = -n f(x) (9)
f(x) (9)
и,
аналогично, вообще
 (10)
(10)
Полученные
соотношения (6) - (10) могут быть объединены в равенстве
f(rx) = r f(x),
f(x),
справедливом
для любого вещественного значения x, каково бы ни было рациональное
число r.
Если
взять здесь x = 1 и обозначить f(1) через c, то
получим
f(r) =
сr.
Таким
образом, мы, собственно говоря установили уже вид функции f, но
пока лишь для рациональных значений аргумента. При этом мы использовали только
тот факт, что функция удовлетворяет условию (3), и не опирались на ее
непрерывность.
Пусть
теперь q будет любое иррациональное значение аргумента. Легко
построить стремящуюся к нему последовательность рациональных чисел r1, r2, …, rn, …
(можно,
например, взять отрезки соответствующей бесконечной десятичной дроби). Мы
только что показали, что
f(rn) = сrn (n = 1,2,…),
Перейдем
здесь к пределу при 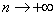 ; справа мы получим сq, слева же,
именно ввиду предположенной непрерывности функции f, получится
; справа мы получим сq, слева же,
именно ввиду предположенной непрерывности функции f, получится
lim f(rn) = f(q),
так
что, окончательно,
f(q) = cq.
Таким
образом, действительно, наша функция при всех вещественных значениях аргумента
выражается формулой (4). Эта формула дает самое общее решение уравнения (3) в
непрерывных функциях.
Вернемся
теперь к уравнению (1). Решим его вначале для вещественно- значных функций.
Итак, рассмотрим уравнение
f(x+y) = f(x) *f(y),
(3)
где
f:  непрерывна.
Нетрудно заметить, что если
непрерывна.
Нетрудно заметить, что если
f(x) = ax (a > 0), (4)
то,
каковы бы ни были два вещественных числа x и у, равенство
(3) всегда имеет место. Оказывается, что функциональным свойством (3), вместе
со свойством непрерывности, показательная функция определяется вполне. Точнее
говоря: единственной функцией, определенной и непрерывной во всем промежутке  и удовлетворяющей в нем условию (3), является
показательная функция (если не считать функции, тождественно равной 0).
и удовлетворяющей в нем условию (3), является
показательная функция (если не считать функции, тождественно равной 0).
Иными
словами, формула (4) - за указанным исключением - дает самое общее решение
функционального уравнения (3) в непрерывных функциях.
Для
доказательства этого рассмотрим произвольную функцию f(x),
определенную и непрерывную при всех x и удовлетворяющую условию (3).
Исключается тривиальный случай, когда f(x)  0.
0.
Итак,
при некотором значении x = х0 эта функция отлична от 0.
Полагая
в (3) у = х0-х, получим
f(x) f(х0-х)
= f(х0)
f(х0-х)
= f(х0)  0;
0;
отсюда
ясно, что f(x) отлична от 0 при всяком х. Больше того, заменяя в
(3) x и у через  , найдем:
, найдем:
f(x) =  ,
,
так
что f(x) всегда строго положительна.
Пользуясь
этим, прологарифмируем равенство (3), например, по натуральному основанию е:
ln f(x+y) = ln f(x)+ln f(y).
Если
положить
 (x)= ln f(x),
(x)= ln f(x),
то
в лице  (x) мы будем иметь функцию, непрерывную (как результат
суперпозиции непрерывных функций, и удовлетворяющую условию:
(x) мы будем иметь функцию, непрерывную (как результат
суперпозиции непрерывных функций, и удовлетворяющую условию:
 (x+y)=
(x+y)=  (x) +
(x) + (y),
(y),
аналогичному
(А). В таком случае, как мы установили, необходимо
 (x)= ln f(x) = cx (с = const.),
(x)= ln f(x) = cx (с = const.),
откуда,
наконец,
f(x) = ecx = ax
(если
положить а = ec), ч. и тр. д.
.4
Полугруппа Sp
.4.1 Определение
и некоторые свойства
Рассмотрим
множество неотрицательных действительных чисел  . Кроме
того, пусть
. Кроме
того, пусть  ,
,  . Введем
здесь алгебраическую операцию следующим образом:
. Введем
здесь алгебраическую операцию следующим образом:
 ,
,  ,
,
(в
дальнейшем будем рассматривать только такие x,y и p).
Обозначим 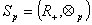 . Справедлива следующая
. Справедлива следующая
Доказательство.
Очевидно, что введенная операция определена на всем множестве 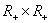 . Заметим, что
. Заметим, что 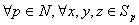

 .
.
 операция
операция  ассоциативна на
ассоциативна на  . Итак,
по определению
. Итак,
по определению  - полугруппа. Заметим также, что указанная операция
коммутативна. Действительно:
- полугруппа. Заметим также, что указанная операция
коммутативна. Действительно:


Тогда
 является абелевой полугруппой.
является абелевой полугруппой.
Установим
наличие у  нулевого элемента
нулевого элемента  .
Нетрудно заметить, что таким элементом является число ноль (
.
Нетрудно заметить, что таким элементом является число ноль ( ), т.к.
), т.к.
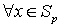
 .
.
Единственность
нуля следует из его единственности в  .
.
Пусть
теперь  ,
,  . Тогда
. Тогда
 ,
,
 ,
,
 .
.
Тогда
получаем, что  обладает правыми сокращениями. Аналогично
показывается, что
обладает правыми сокращениями. Аналогично
показывается, что  обладает и левыми сокращениями, т.е. обладает
сокращениями.
обладает и левыми сокращениями, т.е. обладает
сокращениями.
Таким
образом,  - абелева полугруппа с нулем, обладающая
сокращениями, ч.т.д.
- абелева полугруппа с нулем, обладающая
сокращениями, ч.т.д.
Теперь
найдем группу частных  , если она существует.
, если она существует.
Рассмотрим
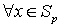 . Пусть
. Пусть  , т.е.
, т.е.  .
.
 .
.
Возможны
следующие два случая:
)
p - нечетное число. В этом случае  . Тогда
. Тогда
 - группа
частных, в которую погружается
- группа
частных, в которую погружается  .
.
2) p -
четное число. Тогда  , где
, где  - один из
p комплексных корней единицы, и группа частных имеет
вид:
- один из
p комплексных корней единицы, и группа частных имеет
вид:
 .
.
Таким образом, справедливо следующее утверждение:
Теорема.
 погружается в группу частных
погружается в группу частных

.4.2 Инвариантная
мера в Sp
Рассмотрим
полугруппу  и попытаемся ввести в ней инвариантную меру. Нетрудно
убедится, что
и попытаемся ввести в ней инвариантную меру. Нетрудно
убедится, что  -алгебра борелевских множеств на
-алгебра борелевских множеств на  является сужением
является сужением  -алгебры
борелевских множеств
-алгебры
борелевских множеств  на
на  , т.е.
, т.е.
 .
.
Теорема.
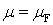 где
где  ,
является
,
является  -аддитивной инвариантной мерой, заданной в полугруппе
-аддитивной инвариантной мерой, заданной в полугруппе  .
.
Доказательство.
Пусть 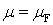 - мера Лебега - Стилтьеса, где
- мера Лебега - Стилтьеса, где  .
.
Она
определена на , а значит, определена и на
, а значит, определена и на  . Очевидно, что
. Очевидно, что  строго
возрастает на
строго
возрастает на . Кроме того, она непрерывна, а значит, непрерывна
слева на всей области определения. Тогда по свойствам меры
. Кроме того, она непрерывна, а значит, непрерывна
слева на всей области определения. Тогда по свойствам меры 
 -аддитивна.
Осталось проверить ее инвариантность.
-аддитивна.
Осталось проверить ее инвариантность.
Докажем,
что данная мера инвариантна слева, т.е. 

 . Ввиду
. Ввиду  -аддитивности
меры
-аддитивности
меры  достаточно показать, что это верно для M = [a;b), где
достаточно показать, что это верно для M = [a;b), где
 . Покажем это.
. Покажем это.
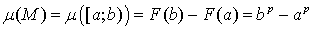 .
.
Заметим,
что  непрерывна как композиция непрерывных функций, а
значит
непрерывна как композиция непрерывных функций, а
значит  . Тогда
. Тогда

 =
=
=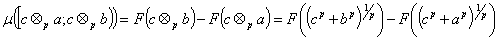 =
=
 .
.
Итак,
данная мера инвариантна слева. Аналогично показывается, что она инвариантна
справа, ч.т.д.
1.4.3 Полухарактеры и характеры в Sp
Теорема.
Отображение  является полухарактером
является полухарактером 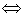
 , где
, где  , а
, а  таково, что
таково, что 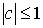 .
.
Доказательство.
1) Пусть  ,
,  непрерывно
как композиция непрерывных отображений; кроме того,
непрерывно
как композиция непрерывных отображений; кроме того, 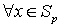
 . Также заметим, что
. Также заметим, что

 ,
,
т.е.
 .
.
Таким
образом,  - полухарактер.
- полухарактер.
)
Пусть теперь  - некоторый полухарактер. Тогда
- некоторый полухарактер. Тогда 
 , т.е.
, т.е.  . Положим
. Положим  ,
,  , g непрерывна как композиция непрерывных функций (φ непрерывна по условию). Тогда
, g непрерывна как композиция непрерывных функций (φ непрерывна по условию). Тогда

 =
= и
и
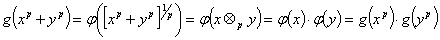 .
.
Выше
было показано (п. 1.3), что в этом случае  , где
, где  .
.
Следовательно,
 , ч.т.д.
, ч.т.д.
Замечание.
Для характеров формулируется и доказывается аналогичная теорема, с той лишь
разницей, что на константу c налагается условие | c | = 1.
.5
Полугруппа S
.5.1 Определение
и некоторые свойства
Рассмотрим
множество:  . Введем на нем алгебраическую операцию следующим
образом:
. Введем на нем алгебраическую операцию следующим
образом:

 .
.
Обозначим
 . Тогда справедливо утверждение:
. Тогда справедливо утверждение:
Лемма.
Множество  является абелевой полугруппой без нулевого элемента и
обладает сокращениями.
является абелевой полугруппой без нулевого элемента и
обладает сокращениями.
Доказательство.
Очевидно, что введенная операция определена на всем множестве . Нетрудно видеть, что
. Нетрудно видеть, что 
 =
=
=
 =
=


 .
.
 операция
операция  ассоциативна на
ассоциативна на  . Тогда
по определению
. Тогда
по определению  - полугруппа. Заметим, указанная операция
коммутативна. Действительно:
- полугруппа. Заметим, указанная операция
коммутативна. Действительно:
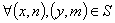

 .
.
Значит,
 является абелевой полугруппой.
является абелевой полугруппой.
В не существует нулевого элемента, т.к. таким элементом
может являться только пара (0,0).
не существует нулевого элемента, т.к. таким элементом
может являться только пара (0,0).
 ,
,
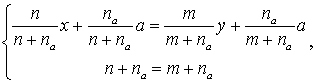


Получаем,
что  обладает правыми сокращениями. Аналогично
показывается, что
обладает правыми сокращениями. Аналогично
показывается, что  обладает и левыми сокращениями, т.е. обладает
сокращениями.
обладает и левыми сокращениями, т.е. обладает
сокращениями.
Итак,
 - абелева полугруппа с нулем, обладающая
сокращениями, ч.т.д.
- абелева полугруппа с нулем, обладающая
сокращениями, ч.т.д.
Замечание.
Наряду с полугруппой  мы также можем рассматривать и полугруппу
мы также можем рассматривать и полугруппу  , для которой верна аналогичная лемма.
, для которой верна аналогичная лемма.
.5.2 Инвариантная
мера в S
Попытаемся
ввести в  инвариантную меру. Нетрудно убедится,
инвариантную меру. Нетрудно убедится,
что
 -алгебра борелевских множеств на
-алгебра борелевских множеств на  является сужением
является сужением  -алгебры
борелевских множеств
-алгебры
борелевских множеств  на
на  , т.е.
, т.е.
 .
.
В
 можно ввести меру Лебега (
можно ввести меру Лебега ( обозначим её
обозначим её  ). Тогда
положим
). Тогда
положим 

 . Заметим, что
. Заметим, что 
 , значит естественно определить:
, значит естественно определить:  .
.  определяется
через меру Лебега, а стало быть является
определяется
через меру Лебега, а стало быть является  -аддитивной
мерой.
-аддитивной
мерой.
В
 существует топология, индуцированная естественной
топологией
существует топология, индуцированная естественной
топологией  . Она является топологической полугруппой, т.к.
отображение
. Она является топологической полугруппой, т.к.
отображение  является непрерывным.
является непрерывным.
Теорема.
 является инвариантной мерой, заданной в полугруппе
является инвариантной мерой, заданной в полугруппе  .
.
Доказательство.
Докажем, что данная мера инвариантна слева, т.е. 

 . Ввиду
. Ввиду  -аддитивности
меры
-аддитивности
меры  достаточно показать, что это верно для M = [a;b)
достаточно показать, что это верно для M = [a;b)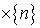 , где
, где  ,
, . Покажем это.
. Покажем это.
 .
.
Т.к.
 непрерывна, то
непрерывна, то 
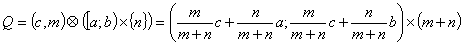
Тогда
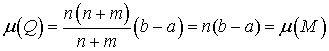 .
.
Итак,
данная мера инвариантна слева. Аналогично показывается, что она инвариантна
справа, ч.т.д.
1.5.3 Полухарактеры и характеры в S
Справедливо следующее утверждение:
Теорема.
Отображение  является полухарактером
является полухарактером 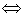
 , где
, где  ,
,  так, что
так, что 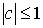 и
и  .
.
Доказательство.
1) Отображение  непрерывно как композиция непрерывных отображений;
кроме того,
непрерывно как композиция непрерывных отображений;
кроме того, 
 и
и  . Также
верно, что
. Также
верно, что 
 . Действительно.
. Действительно.

 .
.
Таким
образом,  - полухарактер.
- полухарактер.
)
Пусть теперь  - некоторый полухарактер. Тогда
- некоторый полухарактер. Тогда 
 , т.е.
, т.е.
 .
.
Заметим,
что 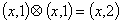 . Обозначим
. Обозначим  , тогда
, тогда 
 . Положим
. Положим  ,
,  , f непрерывна как композиция непрерывных функций (φ непрерывна по условию). Тогда
, f непрерывна как композиция непрерывных функций (φ непрерывна по условию). Тогда 
 ,
,

 и мы
придем к равенству
и мы
придем к равенству

 ,
,
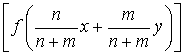
 .
.
Заметим,
что 
 . Тогда
. Тогда 
 т., что
т., что 

 , отсюда
следует, что
, отсюда
следует, что 
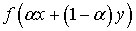
 (f
непрерывна). Это верно
(f
непрерывна). Это верно  . Тогда, положив
. Тогда, положив  ,
получим:
,
получим: 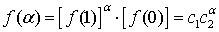 , c=const,
, c=const,  . Тогда
. Тогда 
 .
.
Вернемся
к равенству  . Пусть в нем
. Пусть в нем  , тогда
при
, тогда
при 
 .
.
Если
 , то получаем равенство
, то получаем равенство 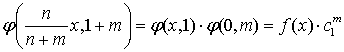 .
.
Тогда
 т., что
т., что  , и,
следовательно,
, и,
следовательно,
 ,
,
Откуда
и получим, что  .
.
Для
отрицательных значений x проводятся аналогичные рассуждения.
Итак
 , ч.т.д.
, ч.т.д.
Замечание.
Если | c | = 1 и | a | = 1, то мы получим
соответствующую теорему для характеров.
2. ОПЕРАТОРЫ ГАНКЕЛЯ
.1 Определения матрицы и оператора Ганкеля
Рассмотрим преобразование числовых последовательностей
 ,
,
связанное
с бесконечной матрицей  . Начальный способ введения оператора Ганкеля состоит
в том, чтобы рассмотреть специальный случай тех преобразований
. Начальный способ введения оператора Ганкеля состоит
в том, чтобы рассмотреть специальный случай тех преобразований  ,у которых каждая из диагоналей, перпендикулярных к
главной диагонали, состоит из одинаковых элементов, т.е.
,у которых каждая из диагоналей, перпендикулярных к
главной диагонали, состоит из одинаковых элементов, т.е. 
 для некоторой числовой последовательности
для некоторой числовой последовательности  . Это приведет нас к следующему определению.
. Это приведет нас к следующему определению.
Определение.
Оператором Ганкеля, действующим из одного пространства последовательностей X в
другое Y,  , называется отображение, которому соответствует
матрица с элементами
, называется отображение, которому соответствует
матрица с элементами
 ,
,  .
.
Матрица
 , элементы которой задаются указанным образом,
называется матрицей Ганкеля:
, элементы которой задаются указанным образом,
называется матрицей Ганкеля:
 .
.
Замечание.
Мы можем переписать это условие в виде равенства операторов. Определим оператор
сдвига

и
его левый обратный
 .
.
Рассмотрим
 , где
, где  ,
является естественным базисом в пространстве числовых последовательностей.
Тогда
,
является естественным базисом в пространстве числовых последовательностей.
Тогда  - n-ый столбик матрицы
- n-ый столбик матрицы  , и
, и 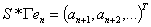 совпадает с
совпадает с  .
Поэтому, следующая простая перестановка на матрице
.
Поэтому, следующая простая перестановка на матрице 
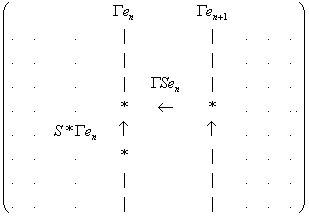
показывает,
что  - оператор Ганкеля тогда и только тогда, когда
- оператор Ганкеля тогда и только тогда, когда

Классическое
пространство, рассматриваемое в теории операторов Ганкеля (и это единственное,
которое мы рассмотрим здесь) - обычное гильбертово пространство
последовательностей
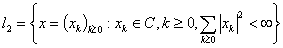 .
.
.2
Ганкелевы операторы в пространствах Харди
Рассмотрим
отображение
 ,
,
где
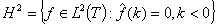 - пространство Харди. Тогда действие оператора S на
- пространство Харди. Тогда действие оператора S на 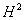 есть умножение на независимую переменную
есть умножение на независимую переменную  :
:
 ,
,
и
действие его левого обратного S* есть действие усеченного оператора умножения
 ,
,
где
 - ортогональная проекция
- ортогональная проекция  . Теперь мы можем рассматривать операторы Ганкеля как
операторы, действующие между пространствами
. Теперь мы можем рассматривать операторы Ганкеля как
операторы, действующие между пространствами 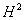 и
и 

 с базисами
с базисами  и
и  . Чтобы сделать это, мы вводим инволюцию
. Чтобы сделать это, мы вводим инволюцию
на
 . Тогда
. Тогда 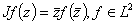 , и в
частности
, и в
частности  .
.
Пусть
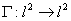 будет оператором Ганкеля. Тогда оператор
будет оператором Ганкеля. Тогда оператор

определяется
матрицей  относительно базисов
относительно базисов  ,
, и удовлетворяет следующему равенству операторов (так
называемое уравнение Ганкеля)
и удовлетворяет следующему равенству операторов (так
называемое уравнение Ганкеля)
 ,
,
(где
 ). Действительно, замечая, что
). Действительно, замечая, что  , мы получим
, мы получим
 .
.
.3
Символы операторов Ганкеля и Теорема Нехари
Теперь
мы рассмотрим характерный пример оператора Ганкеля.
Лемма.
Пусть 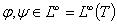 и
и  .
.
Тогда
1)  - ограниченный оператор Ганкеля,
- ограниченный оператор Ганкеля,
)
 ,
,
)
 .
.
Доказательство.
Пусть  и
и  удовлетворяют
условиям леммы. Тогда
удовлетворяют
условиям леммы. Тогда  для всех
для всех  , и
, и

для
 . Следовательно,
. Следовательно,  -
ограниченный оператор Ганкеля. Кроме того, для
-
ограниченный оператор Ганкеля. Кроме того, для  мы имеем
мы имеем
 ,
,
отсюда
 .
.
Ясно,
что это равенство не выполняется для каждого  , если
функция
, если
функция  не голоморфная. Получим
не голоморфная. Получим

для
каждого  ,
,  , и
наконец
, и
наконец
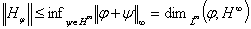 .
.
Лемма
доказана.
Обратное
утверждение также верно. Его называют теоремой Нехари.
Теорема
(З. Нехари, 1957). Если оператор  является
ограниченным оператором Ганкеля, то существует
является
ограниченным оператором Ганкеля, то существует  такой,
что
такой,
что 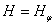 и
и  .
.
ЗАКЛЮЧЕНИЕ
В
данной курсовой работе были рассмотрены две полугруппы, возникающие в
статистических вычислениях и основной пример ганкелевского оператора, изучены
их простейшие свойства. Также решался вопрос о возможности введения
инвариантных мер, велся поиск общего вида полухарактеров, характеров.
полухарактер функция ганкель оператор
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. А.Р. Миротин. Гармонический анализ на абелевых полугруппах. // Под
ред. А.Р. Миротина:- Гомель, ГГУ им. Ф.Скорины, 2008.- 11-12,46-47,207 с.
. А.А. Кириллов, А.Д. Гвишиани. Теоремы и задачи Функционального анализа.
// Под ред. А.А. Кириллова, А.Д. Гвишиани.- М: Наука, 1979.- 132-134,381 с.
. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления.
Том 1.- М: Наука, 1970.- 157-159 с.
4. N.K. Nikolski. Operators, Functions and Systems: An Ecipy
Deaching. Vol. I.- Amer. Math. Sic.- 2002.- 179-182,461 c.