Конечномерные гладкие задачи с равенствами и неравенствами. Принцип Лагранжа
Курсовая
работа
на
тему:
Конечномерные
гладкие задачи с равенствами и неравенствами. Принцип Лагранжа
Оглавление
Введение
Постановка задачи
Необходимые и достаточные условия
экстремума
Принцип Лагранжа
Необходимое условие экстремума II
порядка
Достаточное условие экстремума II
порядка
Правило решения
Теорема Вейерштрасса
Примеры
Список литературы
Введение
Теорию задач на отыскание наибольших и
наименьших величин называют теорией экстремальных задач.
Слово maximum
по латыни означает “наибольшее”, слово minimum
- “наименьшее”. Оба этих понятия объединяются словом “экстремум” (от латинского
extremum, означающего
“крайнее”). Слово “экстремум”, как термин, объединяющий понятия “максимум” и
“минимум”, ввел в употребление Дюбуа-Реймон. Ныне раздел анализа, называют
теорией экстремальных задач.
Запись задачи в виде  означает,
что мы должны решить задачу на минимум, и задачу на максимум.
означает,
что мы должны решить задачу на минимум, и задачу на максимум.
Задачу на максимум всегда можно
свести к задаче на минимум, заменив задачу  задачей
задачей  , где
, где  , и
наоборот. Поэтому в тех случаях, когда формулировки теорем для задач на минимум
и максимум различны, мы иногда ограничиваемся рассмотрением задачи на минимум.
, и
наоборот. Поэтому в тех случаях, когда формулировки теорем для задач на минимум
и максимум различны, мы иногда ограничиваемся рассмотрением задачи на минимум.
Задачи на максимум и минимум
изначально формулируются, как правило, на языке той области, в которой они
возникают. А исследуют их средствами математического анализа. Для того, чтобы
можно было воспользоваться этими средствами, необходимо перевести формулировку
задачи на язык математического анализа. Такой перевод называется формализацией.
В общем виде формализованная задача
выглядит следующим образом : найти экстремум (максимум или минимум) функции  ,определенной
на некотором пространстве
,определенной
на некотором пространстве  при
ограничении
при
ограничении 
 . Кратко
записывается так:
. Кратко
записывается так:

Для функции одной переменной  , для
функции нескольких переменных
, для
функции нескольких переменных  . В более общих случаях
. В более общих случаях  может быть
линейным, нормированным или топологическим пространством. Ограничение
может быть
линейным, нормированным или топологическим пространством. Ограничение  может быть
записано в виде включения, а также в виде уравнений или неравенств.
может быть
записано в виде включения, а также в виде уравнений или неравенств.  - нумерация
(обозначение) задачи (от английского слова problem - задача).
Множество допустимых элементов в задаче
- нумерация
(обозначение) задачи (от английского слова problem - задача).
Множество допустимых элементов в задаче  обозначаем
обозначаем  или
или  . Если
множество допустимых элементов совпадает со всем пространством
. Если
множество допустимых элементов совпадает со всем пространством  , то задачу
, то задачу  называем
задачей без ограничений.
называем
задачей без ограничений.
Решением задачи  на минимум
является точка
на минимум
является точка  такая, что
такая, что  для всех
точек
для всех
точек  . В этом
случае мы пишем
. В этом
случае мы пишем  . Такой
минимум называется еще абсолютным, или глобальным. Аналогично определяется
абсолютный максимум в задаче
. Такой
минимум называется еще абсолютным, или глобальным. Аналогично определяется
абсолютный максимум в задаче  . Величина
. Величина  , где
, где  - решение
задачи, называется численным значением задачи и обозначается
- решение
задачи, называется численным значением задачи и обозначается  или
или  . Множество
решений задачи
. Множество
решений задачи  обозначается
обозначается
 . если
экстремум не достигается, то указывается последовательность точек
. если
экстремум не достигается, то указывается последовательность точек  , на которой
значение функции
, на которой
значение функции  стремиться
к величинам
стремиться
к величинам  и
и  .
.
В связи с каждой экстремальной
задачей возникают вопросы: каковы необходимые условия экстремума, каковы
достаточные условия, существует ли решение задачи, как найти решение явно или
численно.
Одним из важнейших принципов решения
задач с ограничениями является принцип Лагранжа снятие ограничений. Сфера
применимости принципа Лагранжа достаточна широка. Иногда нельзя к задаче
применить имеющуюся теорему, однако этот принцип, примененный без основания,
тем не менее может привести к точкам, среди которых можно выделить решение.
Постановка задачи
Пусть  - функции, n
переменных, отображающие пространство Rn в R. Считаем,
что все функции
- функции, n
переменных, отображающие пространство Rn в R. Считаем,
что все функции  обладают
определенной гладкостью. Гладкой конечномерной экстремальной задачей с
ограничениями тира равенств и неравенств называется следующая задача в Rn :
обладают
определенной гладкостью. Гладкой конечномерной экстремальной задачей с
ограничениями тира равенств и неравенств называется следующая задача в Rn :
 (P)
(P)
В задачах, где имеются ограничения
типа неравенств, важно, рассматриваемая задача на минимум или на максимум. Для
определенности мы будем рассматривать задачу на минимум.
Необходимые и достаточные условия
экстремума
Принцип Лагранжа
Сформулируем необходимое условие
экстремума I порядка в
гладкой конечномерной задаче с ограничениями типа равенств и неравенств -
принцип Лагранжа.
Теорема. Пусть  - точка
локального экстремума в задаче (Р), а функции
- точка
локального экстремума в задаче (Р), а функции  непрерывно дифференцируемы в
окрестности точки
непрерывно дифференцируемы в
окрестности точки  (условие
гладкости). Тогда существует ненулевой вектор множитель Лагранжа
(условие
гладкости). Тогда существует ненулевой вектор множитель Лагранжа  , такой, что
для функции Лагранжа задачи (Р)
, такой, что
для функции Лагранжа задачи (Р)  выполняются условия:
выполняются условия:
a)
стационарности :

b)
дополняющей нежесткости:

c)
неортицательности:

Точки, удовлетворяющие необходимым
условиям локального экстремума, называются критическими. В задаче на максимум 
Необходимое условие экстремума II порядка.
Сформулируем необходимое условие
минимума II порядка в
гладкой конечномерной задаче с ограничениями типа равенств и неравенств.
Теорема. Пусть  - точка
локального минимума в задаче (Р), функции
- точка
локального минимума в задаче (Р), функции  дважды
непрерывно дифференцируемы в некоторой окрестности точки
дважды
непрерывно дифференцируемы в некоторой окрестности точки  (условие
гладкости), векторы
(условие
гладкости), векторы  линейно
независимы (условие регулярности).
линейно
независимы (условие регулярности).
Тогда существует множитель Лагранжа  с
с
 такой, что
для функции Лагранжа задачи (Р)
такой, что
для функции Лагранжа задачи (Р)  выполняются условия экстремума I порядка:
выполняются условия экстремума I порядка:
a) стационарности:

b) дополняющей нежесткости:

c) неотрицательности

и 
где  - конус
допустимых вариаций, а Л - совокупность множителей Лагранжа
- конус
допустимых вариаций, а Л - совокупность множителей Лагранжа  , для
которых выполнены условия a)-c) с
, для
которых выполнены условия a)-c) с  .
.
Мы сформулировали необходимое
условие минимума. Необходимое условие максимума формулируется аналогично, за
исключением того, что множитель Лагранжа  и
соответственно в конусе допустимых вариаций
и
соответственно в конусе допустимых вариаций 
Достаточное условие экстремума II порядка
Сформулируем достаточное условие
минимума II порядка в
гладкой конечномерной задаче с ограничениями типа равенств и неравенств.
Теорема. Пусть функции  , дважды
непрерывно дифференцируемы в некоторой окрестности точки
, дважды
непрерывно дифференцируемы в некоторой окрестности точки  (условие
гладкости), векторы
(условие
гладкости), векторы  -
линейно независимы (условия регулярности), существует множитель Лагранжа
-
линейно независимы (условия регулярности), существует множитель Лагранжа  с
с  такой, что
для функции Лагранжа задачи (Р)
такой, что
для функции Лагранжа задачи (Р)

Выполняются условия экстремума I порядка:
a)
стационарности:

b)
дополняющей нежесткости:

c)
неотрицательности:

и 
с некоторой положительной константой
 , где
, где  - конус
допустимых вариаций, а
- конус
допустимых вариаций, а  -
совокупность множитель Лагранжа
-
совокупность множитель Лагранжа  , для которых выполнены условия a)-c) с
, для которых выполнены условия a)-c) с  .
.
Тогда  - точка локального минимума в задаче
(Р).
- точка локального минимума в задаче
(Р).
Достаточное условие максимума
формулируется аналогично, за исключением того, что множитель Лагранжа  ,
соответственно в конусе допустимых вариаций
,
соответственно в конусе допустимых вариаций  и
и
 .
.
Для решения гладкой конечномерной
задачи с ограничениями типа равенств и неравенств следует:
) Составить функцию Лагранжа 
) Выписать необходимое
условие экстремума I
a) стационарности:

b) дополняющей нежесткости:

c) неотрицательности:

3) Найти точки  ,
удовлетворяющие условиям a)-c) (эти точки
называются критическими).
,
удовлетворяющие условиям a)-c) (эти точки
называются критическими).
При этом отдельно рассмотреть случаи:
a)  ;
;
b)  (или любой
положительной константе);
(или любой
положительной константе);
c)  (или любой
отрицательной константе);
(или любой
отрицательной константе);
В случае a)
критические точки могут доставлять и минимум, и максимум в задаче. В случае b)
критические точки могут доставлять минимум в задаче. В случае c)
критические точки могут доставлять максимум в задаче.
При нахождении критических точек в
условиях дополняющие нежесткости  для каждого
для каждого  надо
рассматривать два случая:
надо
рассматривать два случая:  и
и  .
.
) Исследовать на локальный и
абсолютный экстремум найденные точки или, если их нет, найти  и
и  указать
последовательности допустимых точек, на которых эти абсолютные экстремумы
достигаются.
указать
последовательности допустимых точек, на которых эти абсолютные экстремумы
достигаются.
При этом можно пытаться воспользоваться
непосредственной проверкой или перейти к исследованию условий экстремума II
порядка в каждой критической точке. Отметим, что проверка выполнения
необходимых или достаточных условий экстремума в задаче типа равенств и
неравенств - непростая задача. Поэтому, как правило, мы будем при исследовании
экстремума использовать непосредственную проверку, сравнивая значения
исследуемой функции в критической точке с её значениями в близких допустимых
точках.
Теорема Вейерштрасса
Теорема (конечномерная теорема об обратной
функции). Пусть  - непрерывно
дифференцируемое отображение некоторой окрестности
- непрерывно
дифференцируемое отображение некоторой окрестности  точки
точки
 отличен
от нуля
отличен
от нуля  .
Тогда существует обратное отображение
.
Тогда существует обратное отображение  некоторой
окрестности V точки
некоторой
окрестности V точки  в
окрестность точки
в
окрестность точки  такое, что
такое, что  и
и

с некоторой константой 
Пусть  -
функция n переменных. При
исследовании вопроса о достижении функцией n
переменных экстремума часто используется следующая теорема.
-
функция n переменных. При
исследовании вопроса о достижении функцией n
переменных экстремума часто используется следующая теорема.
Теорема Вейерштрасса. Непрерывная функция на
непустом ограниченном замкнутом подмножестве D
конечномерного пространства (компакте) достигает своих абсолютных максимума и
минимума.
Д о к а з а т е л ь с т в о проведем от
противного. Пусть функция f
(x, y)
при изменении (x, y)
в D оказывается
неограниченной. Тогда для любого n
найдется в D такая точка  ,
что
,
что
 (1)
(1)
Из ограниченной последовательности  можно
извлечь частичная последовательность
можно
извлечь частичная последовательность  ,
сходящуюся к предельной точке
,
сходящуюся к предельной точке 
Отметим, что эта точка  необходимо
принадлежит подмножество D.
Действительно, в противном случае точки
необходимо
принадлежит подмножество D.
Действительно, в противном случае точки  все
были бы от нее отличны, и точка
все
были бы от нее отличны, и точка  была бы точкой
сгущения подмножества D,
ей не принадлежащей, что невозможно ввиду замкнутости подмножества D.
была бы точкой
сгущения подмножества D,
ей не принадлежащей, что невозможно ввиду замкнутости подмножества D.
В следствии непрерывности функции в точке  должно
быть
должно
быть

а это находится в противоречии с (1).
Следствие. Если функция f
непрерывна на  и
и  (
( ),
то она достигает своего абсолютного минимума (максимума) на любом замкнутом
подмножестве из
),
то она достигает своего абсолютного минимума (максимума) на любом замкнутом
подмножестве из  .
.
Напомним, что множество A
в метрическом пространстве называется компактом, если из всякой последовательности
элементов A можно выбрать
сходящуюся к элементу из A
последовательность или (равносильное определение) если из всякого покрытия A
открытыми множествами можно выбрать конечное подпокрытие. Ограниченное и
замкнутое множество конечномерного пространства является компактом.
Примеры.
Пример 1. 
Решение. Функция Лагранжа:

Необходимые условия локального
минимума:
a) стационарности:

b) дополняющей нежесткости:

c) неотрицательности:

Если  , то из уравнения пункта a) выводим,
что
, то из уравнения пункта a) выводим,
что  все
множители Лагранжа - нули, а этого не может быть.
все
множители Лагранжа - нули, а этого не может быть.
Поэтому  , полагаем
, полагаем  .
.
Предположим  , тогда в
силу условия b)
, тогда в
силу условия b)  Выражая из
Выражая из  условия a) через
условия a) через  и
подставляя в уравнения
и
подставляя в уравнения  ,
,  , получим,
что
, получим,
что

экстремум равенство
теорема вейштрасс
откуда  -
противоречие с условием неотрицательности c). Значит, в
случае
-
противоречие с условием неотрицательности c). Значит, в
случае  критических
точек нет.
критических
точек нет.
Пусть . Тогда
. Тогда  -
единственная критическая точка.
-
единственная критическая точка.
Функция  при
при  , значит по
следствию из теорем Вейерштрасса решение задачи существует, а в силу
единственности критической точки решением может быть только она. Итак,
, значит по
следствию из теорем Вейерштрасса решение задачи существует, а в силу
единственности критической точки решением может быть только она. Итак, 
Пример 2.  -
симметричная матрица .
-
симметричная матрица .
Решение 1. Существование решения  очевидно из
теоремы Вейштрасса, ибо сфера
очевидно из
теоремы Вейштрасса, ибо сфера  компактна. Функция Лагранжа:
компактна. Функция Лагранжа:

. Необходимое условие

. Если  ,то
,то  а значит
а значит  , что
противоречит уравнению связи
, что
противоречит уравнению связи  . Положим
. Положим 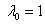 . Тогда
. Тогда  . Таким
образом, решением является собственный вектор матрицы
. Таким
образом, решением является собственный вектор матрицы  .
.
. Домножив соотношения  на
на  , получим,
что
, получим,
что  ; иначе
говоря, решением задачи на минимум будет собственный вектор матрицы
; иначе
говоря, решением задачи на минимум будет собственный вектор матрицы  ,
соответствующий наименьшему собственному значению.
,
соответствующий наименьшему собственному значению.
Пример 3. 
Решение. 1. Функция Лагранжа : 
. Необходимое условие: 
. Если , то
, то  , значит, из предыдущих уравнений
, значит, из предыдущих уравнений  - точка не
является допустимой. Полагаем
- точка не
является допустимой. Полагаем  . Тогда
. Тогда  , или
, или  , или
, или  ,
следовательно,
,
следовательно,  , т.е.
, т.е. 
. По теореме Вейерштрасса существуют
решения задач на минимум и максимум. Рассматривая значения функционала в
стационарных точках, получаем

Список литературы
1. Алексеев
В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации.-1984.
. Галеев
Э.М., Тихомиров В.М. Оптимизация. - 2000.
. Фихтенгольц
Г.М. Курс дифференциального и интегрального исчисления. В 3т. Т.1 - 2003.
. Галеев
Э.М., Тихомиров В.М. Краткий курс теории экстремальных задач. - 1989.