Дифференциальные уравнения
Задача 1. Найти экстремум
функционала  при
при 
Решение
Найдём частные производные
подынтегральной функции:
 ;
;  .
.
Вычислим полную производную по x
от Fy'
по формуле дифференцирования сложной функции:
функция линейное разностное
уравнение экстремум

Имеем  .
.
Составляем дифференциальное
уравнение Эйлера вида:
 .
.
Т.е.  или
или  (1).
(1).
Это ЛНДУ второго порядка с
постоянными коэффициентами. Характеристическое уравнение  -
характеристические числа. Следовательно, общее решение однородного уравнения
будет
-
характеристические числа. Следовательно, общее решение однородного уравнения
будет  . Т.к. мы
имеем неоднородное уравнение со специальной правой частью, частное решение
неоднородного уравнения найдем методом неопределенных коэффициентов. Правая
часть есть многочлен нулевой степени, умноженный на синус, поэтому
. Т.к. мы
имеем неоднородное уравнение со специальной правой частью, частное решение
неоднородного уравнения найдем методом неопределенных коэффициентов. Правая
часть есть многочлен нулевой степени, умноженный на синус, поэтому  . Подставим
это решение в исходное уравнение:
. Подставим
это решение в исходное уравнение:

Тогда общее решение уравнения (1)
имеет вид
 .
.
Для нахождения произвольных
постоянных C1 и C2 подставим
полученное решение в граничные условия:

и тогда уравнение экстремали имеет
вид:
 .
.
Проверим достаточные условия
сильного экстремума:
 .
.
Т.к.  , уравнение Якоби имеет вид:
, уравнение Якоби имеет вид:
 или
или  .
.
Его общее решение есть  .
.
Из условия  , т.е.
, т.е.  , имеем
, имеем  . Т.е. u(x),
удовлетворяющее условию
. Т.е. u(x),
удовлетворяющее условию  , имеет вид
, имеет вид  , где С -
константа. Так как нетривиальное решение
, где С -
константа. Так как нетривиальное решение  уравнения Якоби
уравнения Якоби 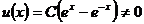 при
при  , то условие
Якоби выполняется.
, то условие
Якоби выполняется.
б) проверим условие Лежандра:
поскольку Fy'y' = 2 > 0
при любых y', то на
кривой  достигается
сильный минимум. Очевидно, на этой же кривой достигается и слабый минимум.
достигается
сильный минимум. Очевидно, на этой же кривой достигается и слабый минимум.
Значение функционала на найденной
экстремали равно примерно -79,3784 (вычислено в математическом пакете Maple).
Ответ:  -79,3784
достигается на кривой
-79,3784
достигается на кривой  .
.
Задача 2. Найти 
Решение
Для вычисления воспользуемся
следующим свойством:
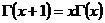
и известным значением гамма-функции
 .
.
Тогда имеем
 ,
,
в свою очередь

и так далее, таким образом, получим,
что
Ответ:  .
.
Задача 3. Найти решение уравнения yk+2 - 19 yk = 4k, y0
= 1, y1 = 1.
Выполнить проверку решения
Решение
Имеем неоднородное линейное
разностное уравнение с постоянными коэффициентами.
Его общее решение имеет вид  , где у
, где у - общее
решение соответствующего однородного уравнения,
- общее
решение соответствующего однородного уравнения,  - какое-нибудь частное решение
неоднородного уравнения.
- какое-нибудь частное решение
неоднородного уравнения.
Характеристическое уравнение
 - характеристические числа. Т.к.
они действительные и различные, то
- характеристические числа. Т.к.
они действительные и различные, то
 .
.
Т.к. мы имеем неоднородное уравнение
со специальной правой частью, частное решение неоднородного уравнения найдем
методом неопределенных коэффициентов. Правая часть есть полином нулевой
степени, умноженный на действительное число степени k, не совпадающее ни с
одним из характеристических чисел, поэтому  . Подставим это решение в исходное
уравнение:
. Подставим это решение в исходное
уравнение:

Следовательно, решение исходного
разностного уравнения есть
 =
= .
.
Произвольные постоянные решения С1
и С2 найдем, используя начальные условия:

 ;
;
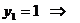
 .
.

Окончательно имеем решение
 .
.
Проверим решение:



Ответ:  .
.